Derivatives of Trigonometric Functions
Last Updated :
16 Jun, 2021
Derivative of a function f(x), is the rate at which the value of the function changes when the input is changed. In this context, x is called the independent variable, and f(x) is called the dependent variable. Derivatives have applications in almost every aspect of our lives. From the rocket launches to our water tank design, derivatives are used by professionals to measure the rate of change and sometimes analyze physical phenomena from a mathematical perspective. Calculating the derivatives of polynomials are pretty simple, trigonometric functions and their derivatives require some extra attention. Let’s see how to calculate them in detail.
Derivatives
The formal and most basic definition of the derivatives involves limits. Geometrically, for a function f(x), derivative at point x represents the slope of a line that is tangent to the curve at that particular point. Using this intuition, the formal definition of the derivatives using the limits was developed. The figure below shows the geometric intuition of the derivatives.

In this figure, notice that the line joining the points (x, f(x)) and (x, f(x + h)) is secant to the figure. But the assumption is that h approaches to zero. So, in this way as the point (x + h) moves closer and closer to the point x, the secant slowly starts becoming a tangent. That’s why it is said that the derivatives are nothing but the slope of the tangents on the curve. Using this logic, first definition of the derivatives is given.
For a function f(x), at a point x = a. The derivative is defined as,
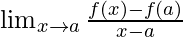
It can also be written as,
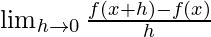
This is the definition of the derivatives. We also denote the derivatives by 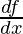 or f'(x).
or f'(x).
Power rule of Derivatives
This is the most commonly used rule in derivatives. It says,
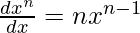
This can be derived through the limit definition of the derivatives.
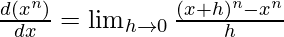
(x + h)n can be opened through binomial expansion,
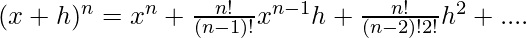
⇒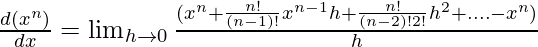
⇒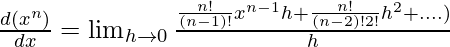
⇒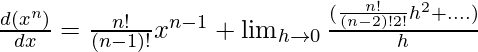
⇒
Question 1: Find the derivative of f(x) = √x.
Solution:
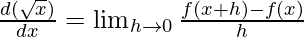
⇒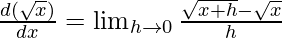
This is indeterminate form, using rationalization
⇒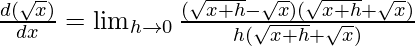
⇒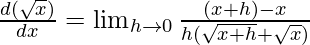
⇒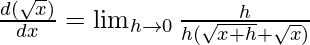
⇒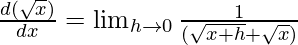
⇒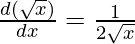
Derivatives of Trigonometric Functions
Derivatives of the trigonometric are first calculated through the limit definition. Before calculating these derivatives and looking at their proofs, it is necessary to revisit some identities of limit related to trigonometric functions.
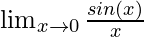
and
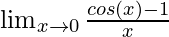
Let’s calculate the derivatives for three most important trigonometric function.
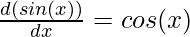
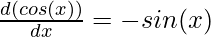
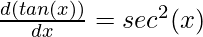
Proving the derivative for sine function
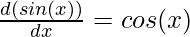
Using the previously mentioned definition of the derivatives
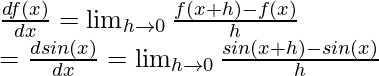
⇒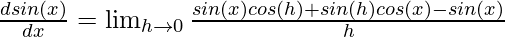
⇒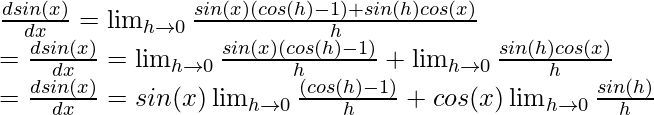
Using the limit identities described above,
⇒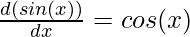
Proving the derivative for cosine function
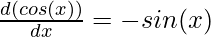
Using the previously mentioned definition of the derivatives
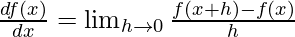
⇒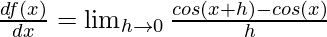
⇒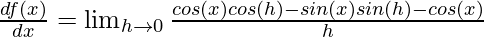
⇒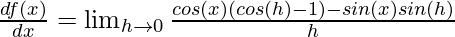
⇒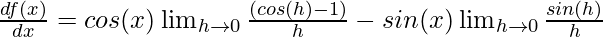
Using the limit identities described above,
⇒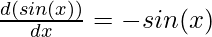
Proving the derivative for tangent function
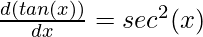
Now that we have the derivatives for the sine and cosine functions. Derivatives of other functions can be calculated simply through Quotient and product rules.
Quotient rule says, for a function f(x) = 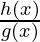 , the derivative of this function is given by,
, the derivative of this function is given by,
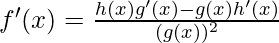
In this case tan(x) = 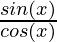
Thus, h(x) = sin(x) and g(x) = cos(x).
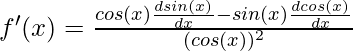
⇒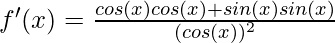
⇒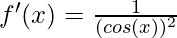
⇒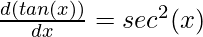
Proving the derivative for secant function
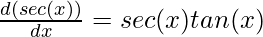
This can be proved easily through chain rule,
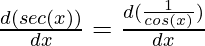
⇒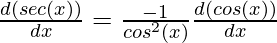
⇒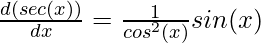
⇒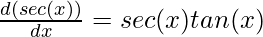
Proving the derivative for co-secant function
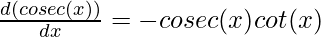
This can be proved easily through chain rule,
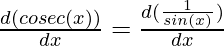
⇒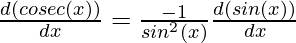
⇒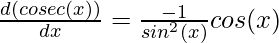
⇒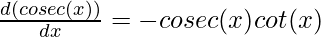
Proof of Product Rule
There are different ways to prove the product rule which includes definition of the derivative and logarithmic differentiation, lets look at the latter way,
y= (f(x)g(x))’ = f'(x)g(x)+ f(x)g'(x)
This can easily be proved by taking the natural log,
ln y’= ln{(f(x)g(x))’} = lnf'(x) + lng'(x)
y’/y= f'(x)/f(x)+ g'(x)/g(x)
![Rendered by QuickLaTeX.com y'=y[\frac{f'(x)g(x)+ g'(x)f(x)}{f(x)g(x)}]\\ y'=f(x)g(x)[\frac{f'(x)g(x)+ g'(x)f(x)}{f(x)g(x)}]\\ y'= f'(x)g(x)+ g'(x)f(x)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b1e3ef1c735f7ee4ae8578a135367b20_l3.png)
Hence, proved.
Let’s look at some sample problems
Sample Problems
Question 1: Find the derivative for the function f(x) at x = 0.
f(x) = sin2(x)
Solution:
This derivative is the combination of power rule and chain rule.
f'(x) = 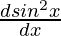
⇒f'(x) = 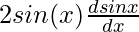
Using the previous results for the derivative of sin(x).
⇒f'(x) = 2sin(x)cos(x)
At x = 0
f'(x) = 0
Question 2: Find the derivative for the function f(x) at x = 0.
f(x) = 5sec(x) + 2cos(x)
Solution:
This derivative is simple
f'(x) = 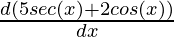
⇒f'(x) = 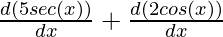
Using the previous results for the derivative of sin(x).
⇒f'(x) = 5sec(x)tan(x) – 2sin(x).
at x = 0
f'(x) = 0
Question 3: Find the derivative for the function f(x) at x = 1.
f(x) = x2 + x4
Solution:
This derivative is simple application of power rule
f'(x) = 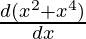
⇒f'(x) = 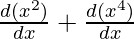
Using the previous results for the derivative of sin(x).
⇒f'(x) = 2x + 4x3
At x = 1
f'(x) = 6
Question 4: Find the derivative for the function f(x).
f(x) = 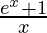
Solution:
This derivative is simple application of quotient rule.
Quotient rule says, for a function f(x) = 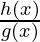 , the derivative of this function is given by,
, the derivative of this function is given by,
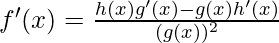
Here h(x) = ex + 1 and g(x) = x
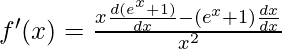
⇒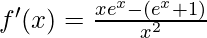
Question 5: Use the Product rule to differentiate the given function,
y = 5xsinx + 4x2cosx
Solution:
Differentiating using Product Rule,
y’= 5sinx + 5xcosx + 8xcosx – 4x2sinx
y’= 5sinx + 13xcosx – 4x2sinx
Share your thoughts in the comments
Please Login to comment...