Question 14. Find the middle terms in the expansion of:
(i) (3x – x3/6)9
Solution:
We have,
(3x – x3/6)9 where, n = 9 (odd number).
So, the middle terms are ((n + 1)/2) = ((9 + 1)/2) = 10/2 = 5 and
((n + 1)/2 + 1) = ((9 + 1)/2 + 1) = (10/2 + 1) = (5 + 1) = 6
The terms are 5th and 6th.
Now,
T5 = T4+1
= 9C4 (3x)9-4 (x3/6)4
= 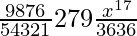
= 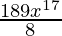
And, T6 = T5+1
= 9C5 (3x)9-5 (x3/6)5
= 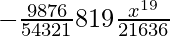
= 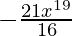
(ii) (2x2 – 1/x)7
Solution:
We have,
(2x2 – 1/x)7 where, n = 7 (odd number).
So the middle terms are ((n + 1)/2) = ((7 + 1)/2) = 8/2 = 4 and
((n + 1)/2 + 1) = ((7 + 1)/2 + 1) = (8/2 + 1) = (4 + 1) = 5
The terms are 4th and 5th.
Now,
T4 = T3+1
= 7C3 (2x2)7-3 (-1/x)3
= -\frac{7×6×5}{3×2}×16x^8×\frac{1}{x^3}
= − 560 x5
And, T5 = T4+1
= 7C4 (2x2)7-4 (-1/x)4
= 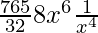
= 280 x2
(iii) (3x – 2/x2)15
Solution:
We have,
(3x – 2/x2)15 where, n = 15 (odd number)
So the middle terms are ((n + 1)/2) = ((15 + 1)/2) = 16/2 = 8 and
((n + 1)/2 + 1) = ((15 + 1)/2 + 1) = (16/2 + 1) = (8 + 1) = 9
The terms are 8th and 9th.
Now,
T8 = T7+1
= 15C7 (3x)15-7 (– 2/x2)7
= 
= 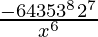
And, T9 = T8+1
= 15C8 (3x)15-8 (– 2/x2)8
= 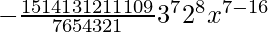
= 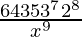
(iv) (x4 – 1/x3)11
Solution:
We have, (x4 – 1/x3)11 where, n = 11 (odd number)
So the middle terms are ((n + 1)/2) = ((11 + 1)/2) = 12/2 = 6 and
((n + 1)/2 + 1) = ((11 + 1)/2 + 1) = (12/2 + 1) = (6 + 1) = 7
The terms are 6th and 7th.
Now,
T6 = T5+1
= 11C5 (x4)11-5 (1/x3)5
= 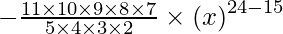
= -462 x9
And, T7 = T6+1
= 11C6 (x4)11-6 (1/x3)6
= 
= 462 x2
Question 15. Find the middle terms in the expansion of:
(i) (x – 1/x)10
Solution:
We have,
(x – 1/x)10 where, n = 10 (even number)
So the middle term is (n/2 + 1) = (10/2 + 1) = (5 + 1) = 6th term
Now,
T6 = T5+1
= 10C5 (x)10-5 (–1/x)5
= 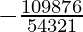
= −252
(ii) (1 – 2x + x2)n
Solution:
We have, (1 – 2x + x2)n
= (1 – x)2n
Here, n is an even number.
So the middle terms is 2n/2 + 1 = (n + 1)th term
Now,
Tn+1 = 2nCn (-1)n xn
= 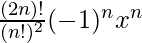
(iii) (1 + 3x + 3 x2 + x3)2n
Solution:
We have, (1 + 3x + 3 x2 + x3)2n
= (1 + x )6n
Here, n is an even number.
So the middle terms is (6n/2 + 1) = (3n + 1)th term
Now,
T3n+1 = 6nC3n x3n
= 
(iv) (2x – x2/4)9
Solution:
We have,
(2x – x2/4)9 where, n = 9 (odd number)
So the middle terms are ((n + 1)/2) = ((9 + 1)/2) = 10/2 = 5 and
((n + 1)/2 + 1) = ((9 + 1)/2 + 1) = (10/2 + 1) = (5 + 1) = 6
The terms are 5th and 6th.
Now,
T5 = T4+1
= 9C4 (2x)9-4 (–x2/4)4
= 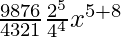
= 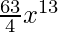
And, T6 = T5+1
= 9C5 (2x)9-5 (–x2/4)5
= 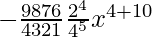
= 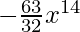
(v) (x – 1/x)2n+1
Solution:
We have, (x – 1/x)2n+1
Here, 2n + 1 is an odd number.
So the middle terms are((2n + 1 + 1)/2)th and ((2n + 1 + 1)/2 + 1)th terms.
The terms are (n + 1)th and (n + 2)th
Now
Tn+1 = 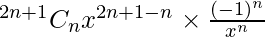
=(-1)n 2n+1Cn x
And Tn+2 = Tn+1+1
= 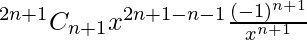
= 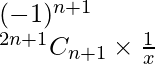
(vi) (x/3 + 9y)10
Solution:
We have,
(x/3 + 9y)10 where, n = 10 (even number)
So the middle term is (n/2 + 1) = (10/2 + 1) = (5 + 1) = 6th term.
Now,
T6 = T5+1
= 10C5 (x/3)10-5 (9y)5
= 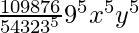
= 61236 x5 y5
(vii) (3 – x3/6)7
Solution:
We have,
(3 – x3/6)7 where, n = 7 (odd number).
So the middle terms are ((n + 1)/2) = ((7 + 1)/2) = 8/2 = 4 and
((n + 1)/2 + 1) = ((7 + 1)/2 + 1) = (8/2 + 1) = (4 + 1) = 5
The terms are 4th and 5th.
Now,
T4 = T3+1
= 7C3 (3)7-3 (-x3/6)3
= 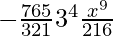
= 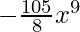
And, T5 = T4+1
= 9C4 (3)9-4 (-x3/6)4
= 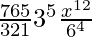
= 
(viii) (2ax – b/x2)12
Solution:
We have,
(2ax – b/x2)12 where, n = 12 (even number).
So the middle terms are (n/2 + 1) = (12/2 + 1) = 7th term
Now,
T7 = T6+1
= 12C6 (2ax)12-6 (-b/x2)6
= 12C6 (2ax)6 (b/x2)6
= 12C6 (26a6x6)(b6/x12)
= 12C6 (26a6b6/x6)
(ix) (p/x + x/p)9
Solution:
We have,
(p/x + x/p)9 where, n = 9 (odd number).
So the middle terms are ((n + 1)/2) = ((9 + 1)/2) = 10/2 = 5 and
((n + 1)/2 + 1) = ((9 + 1)/2 + 1) = (10/2 + 1) = (5 + 1) = 6
The terms are 5th and 6th.
Now,
T5 = T4+1
= 9C4 (p/x)9-4 (x3/p)4
= 9C4 (p/x)5 (x/p)4
= 9C4 (p/x)
And, T6 = T5+1
= 9C5 (p/x)9-5 (x/p)5
= 9C5 (p/x)4(x/p)5
= 9C5 (x/p)
(x) (x/a – a/x)10
Solution:
We have,
(x/a – a/x)10 where, n = 10 (even number).
So the middle terms are (n/2 + 1) = (10/2 + 1) 6th term
Now,
T6 = T5+1
= 10C5 (x/a)10-5 (-a/x)5
= –10C5 (x/a)5 (a/x)5
= –10C5
= -252
Question 16. Find the term independent of x in the expansion of the following expressions:
(i) (3/2 x2 – 1/3x)9
Solution:
We have,
(3/2 x2 – 1/3x)9
We know, the (r+1)th term of the expression is given by,
Tr+1 = nCr xn-r ar
= 9Cr (3/2x2)9-r (-1/3x)r
= 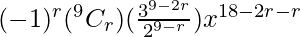
For this term to be independent of x, we must have
=> 18 – 3r = 0
=> 3r = 18
=> r = 18/3
=> r = 6
So, the required term is 7th term.
So, T7 = T6+1
= 9C6 × (39-12)/(29-6)
= 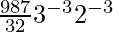
= 7/18
Hence, the term independent of x is 7/18.
(ii) (2x + 1/3x2)9
Solution:
We have,
(2x + 1/3x2)9
We know, the (r+1)th term of the expression is given by,
Tr+1 = nCr xn-r ar
= 9Cr (2x)9-r (1/3x2)r
= 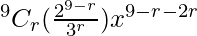
For this term to be independent of x, we must have
=> 9 – 3r = 0
=> r = 3
So, the required term is 4th term.
So, T7 = T6+1
= 9C6 × (29-3)/(33)
= 
= 5376/27
(iii) (2x2 – 3/x3)25
Solution:
We have,
(2x2 – 3/x3)25
We know, the (r+1)th term of the expression is given by,
Tr+1 = nCr xn-r ar
= 25Cr (2x2)25-r (-3/x3)r
= (-1)r 25Cr × 225-r × 3r x50-2r-3r
For this term to be independent of x, we must have
=> 50 – 5r = 0
=> 5r = 50
=> r = 10
So, the required term is 11th term.
So, T11 = T10+1
= (-1)10 25C10 × 225-10 × 310
= 25C10 (215 × 310)
(iv) (3x – 2/x2)15
Solution:
We have,
(3x – 2/x2)15
We know, the (r+1)th term of the expression is given by,
Tr+1 = nCr xn-r ar
= 15Cr (3x)15-r (-2/x2)r
= (-1)r 15Cr × 315-r × 2r x15-r-2r
For this term to be independent of x, we must have
=> 15 – 3r = 0
=> 3r = 15
=> r = 5
So, the required term is 6th term.
So, T6 = T5+1
= (-1)5 15C5 × 315-5 × 25
= −3003 × 310 × 25
(v) 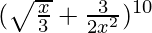
Solution:
We have
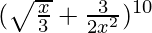
We know, the (r+1)th term of the expression is given by,
Now,
Tr+1 = 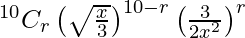
= 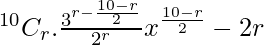
For this term to be independent of x, we must have
=> (10-r)/2 – 2r = 0
=> 10 – 5r = 0
=> r = 2
So, the required term is 3th term.
So, T3 = T2+1
T3 = 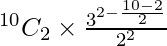
= 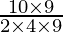
= 5/4
(vi) 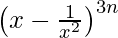
Solution:
We have
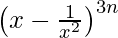
We know, the (r+1)th term of the expression is given by,
Now,
Tr+1 = 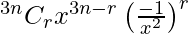
= (-1)r 3nCr x3n-r-2r ar
For this term to be independent of x, we must have}
=> 3n – 3r = 0
=> r = n
So, the required term is (n + 1)th term.
So,
Tn+1 = (-1)n 3nCn
(vii) 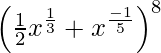
Solution:
We have
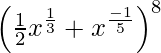
We know, the (r+1)th term of the expression is given by,
Now,
Tr+1 = 
= 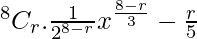
For this term to be independent of x, we must have
=> (8 – r)/3 – r/5 = 0
=> 40 – 5r – 3r = 0
=> 8r = 40
=> r = 5
So, the required term is 6th term.
So, T6 = T5+1
T6 = 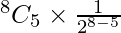
= 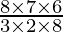
= 7
(viii) (1 + x + 2x3) (3/2x2 – 3/3x)9
Solution:
We have
(1 + x + 2x3) (3/2x2 – 3/3x)9
We know, the (r+1)th term of the expression is given by,
Now,
Tr+1 = (1 + x + 2x3) [(3/2x2) – 9C1 (3/2x2)8 (1/3x) + . . . – 9C7 (3/2x2)2 (1/3x)7]
For this term to be independent of r, we must have
= 9C6 (33/23) (1/36) – 2x3 9C7 (23/33) (1/37) (1/x3)
= 7/18 – 2/27
= (189 – 36)/486
= 153/486
= 17/54
(ix) ![Rendered by QuickLaTeX.com \left( \sqrt[3]{x} + \frac{1}{2 \sqrt[3]{x}} \right)^{18}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d2df87f5fbf27b1855af3d48b3cc8dbd_l3.png) , x > 0
, x > 0
Solution:
We have
![Rendered by QuickLaTeX.com \left( \sqrt[3]{x} + \frac{1}{2 \sqrt[3]{x}} \right)^{18}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d2df87f5fbf27b1855af3d48b3cc8dbd_l3.png)
We know, the (r+1)th term of the expression is given by,
Now,
Tr+1 = 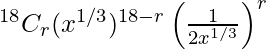
= 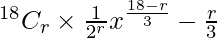
For this term to be independent of r, we must have
=> (18 – r)/3 – r/3 = 0
=> 18 – 2r = 0
=> r = 9
So, the required term is 9th term.
So, T9 = T8+1
T9 = 18C9 (1/29)
(x) 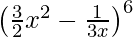
Solution:
We have
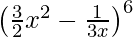
Suppose the (r + 1)th term in the given expression is independent of x.
Now,
Tr+1 = 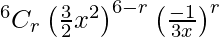
= 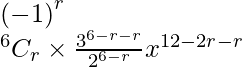
For this term to be independent of x, we must have
=> 12 – 3r = 0
=> r = 4
Hence, the required term is the 4th term.
So, T4 = T3+1
= 
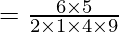
= 5/12
Question 17. If the coefficients of (2r + 4)th and (r – 2)th terms in the expansion of (1 + x)18 are equal, find r.
Solution:
We are given,
(1 + x)18
We know, the coefficient of the rth term in the expansion of (1 + x)n is nCr-1.
So, the coefficients of the (2r + 4)th and (r – 2)th terms in the given expansion are,
18C2r+4-1 and 18Cr-2-1
According to the question, we have,
=> 18C2r+4-1 = 18Cr-2-1
=> 18C2r+3 = 18Cr-3
We know if nCr = nCs , then r = s or r + s = n.
=> 2r + 3 = r – 3 or 2r + 3 + r – 3 = 18
=> 2r – r = –3 – 3 or 3r = 18 – 3 + 3
=> r = –6 or 3r = 18
=> r = –6 or r = 6
Ignoring r = – 6 as r cannot be negative.
Therefore, the value of r is 6.
Question 18. If the coefficients of (2r + 1)th term and (r + 2)th term in the expansion of (1 + x)43 are equal, find r.
Solution:
We are given,
(1 + x)43
We know, the coefficient of the rth term in the expansion of (1 + x)n is nCr-1.
So, the coefficients of the (2r + 1)th and (r + 2)th terms in the given expansion are,
43C2r+1-1 and 43Cr+2-1
According to the question, we have,
=> 43C2r+1-1 = 43Cr+2-1
=> 43C2r = 43Cr+1
We know if nCr = nCs , then r = s or r + s = n.
=> 2r = r + 1 or 2r + r + 1 = 43
=> r = 1 or 3r = 42
=> r = 1 or r = 14
Ignoring r = 1 as it gives the same term on both the sides.
Therefore, the value of r is 14.
Question 19. Prove that the coefficient of (r + 1)th term in the expansion of (1 + x)n+1 is equal to the sum of the coefficients of rth and (r+1)th terms in the expansion of (1 + x)n.
Solution:
We know, the coefficients of (r + 1)th term in (1 + x)n+1 is n+1Cr.
So, sum of the coefficients of the rth and (r + 1)th terms in (1 + x)n is,
(1 + x)n = nCr-1 + nCr
As, nCr+1 + nCr = n+1Cr+1
= n+1Cr
Hence proved.
Question 20. Prove that the term independent of x in the expansion of (x + 1/x)2n is 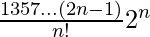 .
.
Solution:
We have,
(x + 1/x)2n
We know the (r + 1)th term is given by,
Tr+1 = nCr xn-r ar
= 2nCr x2n-r (1/x)r
= 2nCr x2n-2r
For this term to be independent of x, we must have,
=> 2n − 2r = 0
=> 2n = 2r
=> r = n
Therefore, the required term is (n+1)th term .
Tn+1 = 2nCn x2n-n (1/x)n
= 2nCn
= 
= 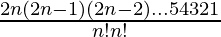
= 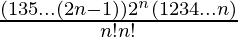
= 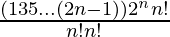
= 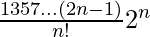
Hence proved.
Question 21. If the coefficients of 5th, 6th and 7th terms of the expansion (1 + x)n are in A.P., find n.
Solution:
We have, (1 + x)n
We know the coefficient of rth term of a binomial expression is given by nCr-1.
Coefficient of 5th term = nC5-1 = nC4
Coefficient of 6th term = nC6-1 = nC5
Coefficient of 7th term = nC7-1 = nC6
According to the question, we have,
=> 2 nC5 = nC4 + nC6
=> ![Rendered by QuickLaTeX.com 2[\frac{n!}{(n-5)!5!}] = \frac{n!}{(n-4)!4!} + \frac{n!}{(n-6)!6!}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a774154edd0675921b368a9d276d5d4a_l3.png)
=> 
=> 
=> 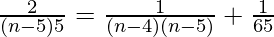
=> 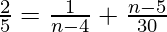
=> 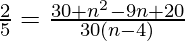
=> 60(n−4) = 150 + 5n2 − 45n + 100
=> 60n − 240 = 250 + 5n2 − 45n
=> 5n2 − 105n + 490 = 0
=> n2 − 21n + 98 = 0
=> n2 − 7n − 14n + 98 = 0
=> n (n − 7) − 14 (n − 7) = 0
=> (n − 7) (n − 14) = 0
=> n = 7 or n = 14
Therefore, the value of n is 7 or 14.
Question 22. If the coefficients of 2nd, 3rd, and 4th terms of the expansion (1 + x)2n are in A.P., show that 2n2 − 9n + 7 = 0.
Solution:
We have, (1 + x)2n
We know the coefficient of rth term of a binomial expression is given by nCr-1.
Coefficient of 2nd term = 2nC2-1 = 2nC1
Coefficient of 3rd term = 2nC3-1 = 2nC2
Coefficient of 4th term = 2nC4-1 = 2nC3
According to the question, we have,
=> 2 2nC2 = 2nC1 + 2nC3
=> 2 = 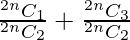
=> 2 = 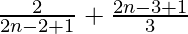
=> 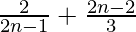 = 2
= 2
=> 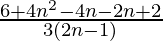 = 2
= 2
=> 4n2 − 6n + 8 = 12n − 6
=> 4n2 − 18n + 14 = 0
=> 2 (2n2 − 9n + 7) = 0
=> 2n2 − 9n + 7 = 0
Hence proved.
Question 23. In the expansion of (1 + x)n, the binomial coefficients of three consecutive terms are respectively 220, 495, and 792, find the value of n.
Solution:
We have, (1 + x)n
Let the three consecutive terms be rth, (r+1)th and (r+2)th.
We know the coefficient of rth term of a binomial expression is given by nCr-1.
Coefficient of rth term = nCr-1 = 220
Coefficient of (r+1)th term = nCr+1-1 = nCr = 495
Coefficient of (r+2)th term = nCr+2-1 = nCr+1 = 792
Now, 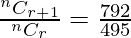
=> 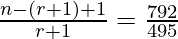
=> 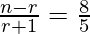
=> 5n − 5r = 8r + 8
=> 5n − 13r = 8 . . . . (1)
Also, 
=> 
=> 4n − 4r + 4 = 9r
=> 4n − 13r = −4 . . . . (2)
Subtracting (2) from (1), we get,
=> n = 8 + 4
=> n = 12
Therefore, the value of n is 12.
Question 24. If the coefficients of 2nd, 3rd and 4th terms of the expansion (1 + x)n are in A.P., then find the value of n.
Solution:
We have, (1 + x)n
We know the coefficient of rth term of a binomial expression is given by nCr-1.
Coefficient of 2nd term = nC2-1 = nC1
Coefficient of 3rd term = nC3-1 = nC2
Coefficient of 4th term = nC4-1 = nC3
According to the question, we have,
=> 2 nC2 = nC1 + nC3
=> 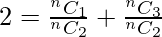
=> 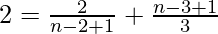
=> 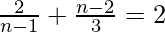
=> 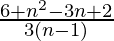 = 2
= 2
=> n2 − 3n + 8 = 6 (n − 1)
=> n2 − 3n + 8 = 6n − 6
=> n2 − 9n + 14 = 0
=> n2 − 7n − 2n + 14 = 0
=> n (n−7) − 2 (n−7) = 0
=> (n − 2) (n − 7) = 0
=> n = 2 or n = 7
Ignoring n = 2 as it does not satisfy our condition.
Therefore, the value of n is 7.
Question 25. If in the expansion of (1 + x)n, the coefficients of pth and qth terms are equal, then prove that p + q = n + 2, where p ≠ q.
Solution:
We have, (1 + x)n
We know the coefficient of rth term of a binomial expression is given by nCr-1.
Coefficient of pth term = nCp-1
Coefficient of qth term = nCq-1
According to the question, we have,
=> nCp-1 = nCq-1
=> p − 1 = q − 1 or p − 1 + q − 1 = n
=> p = q or p + q − 2 = n
=> p + q − 2 = n
=> p + q = n + 2
Hence proved.
Question 26. If in the expansion of (1 + x)n, the binomial coefficients of three consecutive terms are respectively 56, 70, and 56, find n and the position of the terms of these coefficients.
Solution:
We have, (1 + x)n
Let the three consecutive terms be rth, (r+1)th and (r+2)th.
We know the coefficient of rth term of a binomial expression is given by nCr-1.
Coefficient of rth term = nCr-1 = 56
Coefficient of (r+1)th term = nCr+1-1 = nCr = 70
Coefficient of (r+2)th term = nCr+2-1 = nCr+1 = 56
Now, 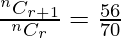
=> 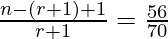
=> 
=> 5n − 5r = 4r + 4
=> 5n − 9r = 4 . . . . (1)
Also, 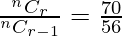
=> 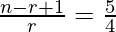
=> 4n − 4r + 4 = 5r
=> 4n − r = −4 . . . . (2)
Subtracting (2) from (1), we get,
=> n = 4 + 4
=> n = 8
Putting n = 8 in (1), we get,
=> 5(8) − 9r = 4
=> 40 − 9r = 4
=> 9r = 36
=> r = 4
Therefore, three consecutive terms are 4th, 5th and 6th terms.
Share your thoughts in the comments
Please Login to comment...