Class 11 RD Sharma Solutions – Chapter 32 Statistics – Exercise 32.2

Question 1. Calculate the mean deviation from the median of the following frequency distribution:

Heights in inches	58	59	60	61	62	63	64	65	66
No. Of Students	15	20	32	35	35	22	20	10	8

Solution:

Median is the middle term of the observation in ascending order,

So, Median = 61

Let us assume, 

x_i =Heights in inches

f_i = Number of students

xi	fi	Cumulative Frequency	|di| = |xi – M| = |xi – 61|	fi |di|
58	15	15	3	45
59	20	35	2	40
60	32	67	1	32
61	35	102	0	0
62	35	137	1	35
63	22	159	2	44
64	20	179	3	60
65	10	189	4	40
66	8	197	5	40
	N = 197			Total = 336

N=197

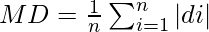
= 1/197 × 336

= 1.70

Therefore, the mean deviation is 1.70.

Question 2. The number of telephone calls received at an exchange in 245 successive on2-minute intervals is shown in the following frequency distribution:

Number of calls	0	1	2	3	4	5	6	7
Frequency	14	21	25	43	51	40	39	12

Compute the mean deviation about the median.

Solution:

Median is the middle term of the observation in ascending order,

We know, Median is the even term, (3+5)/2 = 4

So, Median = 8

Let us assume

x_i =Number of calls

f_i = Frequency

N = 245

xi	fi	Cumulative Frequency	|di| = |xi – M| = |xi – 61|	fi |di|
0	14	14	4	56
1	21	35	3	63
2	25	60	2	50
3	43	103	1	43
4	51	154	0	0
5	40	194	1	40
6	39	233	2	78
7	12	245	3	36
	Total = 245			Total = 366

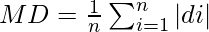
= 1/245 × 336

= 1.49

Therefore, mean deviation is 1.49.

Question 3. Calculate the mean deviation about the median of the following frequency distribution:

xi	5	7	9	11	13	15	17
fi	2	4	6	8	10	12	8

Solution:

Calculating the median,

We know, Number of observations, N = 50

Median = (50)/2 = 25

Therefore, the median corresponding to 25 is 13.

xi	fi	Cumulative Frequency	|di| = |xi – M| = |xi – 61|	fi |di|
5	2	2	8	16
7	4	6	6	24
9	6	12	4	24
11	8	20	2	16
13	10	30	0	0
15	12	42	2	24
17	8	50	4	32
	Total = 50			Total = 136

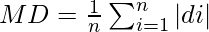
= 1/50 × 136

= 2.72

Therefore, the mean deviation is 2.72.

Question 4. Find the mean deviation from the mean for the following data:

(i)

xi	5	7	9	10	12	15
fi	8	6	2	2	2	6

(ii)

xi	5	10	15	20	25
fi	7	4	6	3	5

(iii)

xi	10	30	50	70	90
fi	4	24	28	16	8

Solution:

(i) We know,

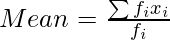
xi	fi	Cumulative Frequency (xifi)	|di| = |xi – Mean|	fi |di|
5	8	40	4	32
7	6	42	2	12
9	2	18	0	0
10	2	20	1	2
12	2	24	3	6
15	6	90	6	36
	Total = 26	Total = 234		Total = 88

Now, Mean = 234/26

= 9

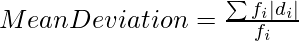
= 88/26

= 3.3

∴ The mean deviation is 3.3

(ii) We know,

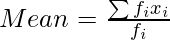
xi	fi	Cumulative Frequency (xifi)	|di| = |xi – Mean|	fi |di|
5	7	35	9	63
10	4	40	4	16
15	6	90	1	6
20	3	60	6	18
25	5	125	11	55
	Total = 25	Total = 350		Total = 158

Mean = 350/25

= 14

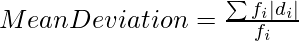
= 158/25

= 6.32

∴ The mean deviation is 6.32

(iii) We know,

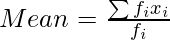
= 4000/80

= 50

xi	fi	Cumulative Frequency (xifi)	|di| = |xi – Mean|	fi |di|
10	4	40	40	160
30	24	720	20	480
50	28	1400	0	0
70	16	1120	20	320
90	8	720	40	320
	Total = 80	Total = 4000		Total = 1280

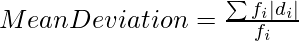
= 1280/80

= 16

∴ The mean deviation is 16

Question 5. Find the mean deviation from the median for the following data :

(i)

xi	15	21	27	30
fi	3	5	6	7

(ii)

xi	74	89	42	54	91	94	35
fi	20	12	2	4	5	3	4

(iii)

Marks obtained	10	11	12	14	15
No. of students	2	3	8	3	4

Solution:

(i) We know, 

Number of observations, N = 21

Median = (21)/2 = 10.5

Therefore, the median corresponding to 10.5 is 27

xi	fi	Cumulative Frequency	|di| = |xi – M|	fi |di|
15	3	3	15	45
21	5	8	9	45
27	6	14	3	18
30	7	21	0	0
	Total = 21	Total = 46		Total = 108

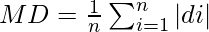
= 1/21 × 108

= 5.14

∴ The mean deviation is 5.14

(ii) We know, 

Number of observations, N =50

Median = (50)/2 = 25

Therefore, the median corresponding to 25 is 74.

xi	fi	Cumulative Frequency	|di| = |xi – M|	fi |di|
74	20	4	39	156
89	12	6	32	64
42	2	10	20	80
54	4	30	0	0
91	5	42	15	180
94	3	47	17	85
35	4	50	20	60
	Total = 50	Total = 189		Total = 625

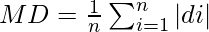
= 1/50 × 625

= 12.5

Therefore, the mean deviation is 12.5

(iii) We know, 

Number of observations, N =20

Median = (20)/2 = 10

So, the median corresponding to 10 is 12.

xi	fi	Cumulative Frequency	|di| = |xi – M|	fi |di|
10	2	2	2	4
11	3	5	1	3
12	8	13	0	0
14	3	16	2	6
15	4	20	3	12
	Total = 20			Total = 25

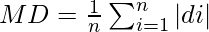
= 1/20 × 25

= 1.25

∴ The mean deviation is 1.25