Class 11 RD Sharma Solutions – Chapter 9 Trigonometric Ratios of Multiple and Submultiple Angles – Exercise 9.1 | Set 1
Last Updated :
09 Mar, 2022
Prove the following identities:
Question 1. √[(1 – cos2x)/(1 + cos2x)] = tanx
Solution:
Let us solve LHS,
= √[(1 – cos2x)/(1 + cos2x)]
As we know that, cos2x =1 – 2 sin2x
= 2 cos2x – 1
So,
= √[(1 – cos2x)/(1 + cos2x)]
= √[(1 – (1 – 2sin2x))/(1 + (2cos2x – 1))]
= √(1 – 1 + 2sin2x)/(1 + 2cos2x – 1)1
= √[2 sin2x/2 cos2x]
= sinx / cosx
= tanx
LHS = RHS
Hence proved.
Question 2. sin2x/(1 – cos2x) = cotx
Solution:
Let us solve LHS,
= sin 2x/(1 – cos 2x)
As we know that,
cos 2x = 1 – 2 sin2x
Sin 2x = 2 sin x cos x
So,
sin 2x/(1-cos 2x) = (2 sin x cos x)/(1 – (1 – 2sin2x))
= (2 sin x cos x)/(1 – 1 + 2sin2x)]
= [2 sin x cos x/2 sin2x]
= cos x/sin x
= cot x
LHS = RHS
Hence proved.
Question 3. sin 2x/(1 + cos 2x) = tan x
Solution:
Let us solve LHS,
= sin 2x / (1+cos 2x)
As we know that,
cos 2x = 1 – 2 sin2x
= 2 cos2x – 1
sin 2x = 2 sin x cos x
So,
sin 2x / (1 + cos2x) = [2 sin x cos x / (1 + (2cos2x – 1))]
= [2 sin x cos x / (1+2cos2x – 1)]
= [2 sin x cos x/2 cos2x]
= sin x/cos x
= tan x
LHS = RHS
Hence proved.
Question 4. 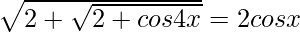 , 0 < r < π/4
, 0 < r < π/4
Solution:
Let us solve LHS,
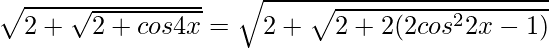
As we know that,
cos 2x = 2 cos2x – 1 ⇒ cos 4x = 2 cos22x – 1
So,
= 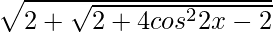
= 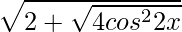
= 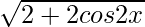
= 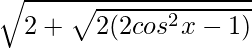
= 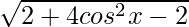
= 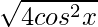
= 2 cos x
LHS = RHS
Hence proved.
Question 5. [1 – cos 2x + sin 2x]/[1 + cos 2x + sin 2x] = tan x
Solution:
Let us solve LHS,
= [1 – cos 2x + sin 2x]/[1 + cos 2x + sin 2x]
As we know that,
cos 2x = 1 – 2 sin2x
= 2 cos2x – 1
sin 2x = 2 sin x cos x
So,
= {1 – (1 – 2sin2x) + 2sinxcosx} / {1 + (2 cos2x – 1) + 2 sin x cosx}
= {1 − 1 + 2sin2x + 2sinxcosx} / {1 + 2cos2x − 1 + 2sinx cosx}
= {2 sin2x + 2sinxcosx} / {2 cos2x + 2sinxcosx}
= {2sinx (sinx + cosx)} / {2 cos x (cosx + sin x)}
= sinx/cosx
= tan x
LHS = RHS
Hence proved.
Question 6. [sin x + sin 2x]/[1 + cos x + cos2x] = tanx
Solution:
Let us solve LHS,
= [sin x + sin 2x]/[1 + cos x + cos 2x]
As we know that,
cos 2x = cos2x sin2x
sin 2x = 2 sin x cos x
So,
{sin x + sin 2x} / {1 + cos x + cos 2x} = {sin x + 2 sin x cos x} / {1 + cosx + (2cos2x − 1)}
= {sinx + 2 sinx cos x} / {1 + cosx + 2cos2x − 1}
= {sin x + 2 sin x cosx} / {cosx + 2cos2x}
= {sinx (1 + 2 cos x)} / {cosx(1 + 2cosx)}
= sinx / cosx
= tan x
LHS = RHS
Hence proved.
Question 7. cos 2x / (1+ sin 2x) = tan (π/4 – x)
Solution:
Let us solve LHS,
= cos 2x / (1 + sin 2x)
As we know that,
cos 2x = cos2x – sin2x
sin 2x = 2 sin x cos x
So,
{cos 2x} / {1 + sin 2x} = {cos2x – sin2x} / {1 + 2 sin x cos x}
= {(cosx – sinx)(cosx + sinx)} / {sin2x + cos2x + 2 sin x cos x}
Since, a2 – b2 = (a – b)(a + b) and sin2x + cos2x = 1
So,
= {(cosx – sinx)(cosx + sinx)} / {(sinx + cos x)2
Since, a2+ b2 + 2ab = (a + b)2
So,
= {(cosx – sinx)(cosx + sinx)} / {(sinx + cosx)(sinx + cosx)}
= (cosx – sinx) / (sin x + cos x)
Now multiplying numerator and denominator by 1/√2, we get,
= 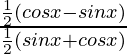
= 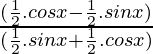
= 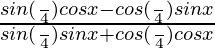
Since, 1/√2 = sin π/4, so
= 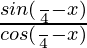
By using the formulas, we get
sin(A – B) = sinA cosB – sinB cosA
cos(A – B)= cosA cosB + sinA sinB
= tan (π/4 – x)
LHS = RHS
Hence proved.
Question 8. cos x/(1 – sin x) = tan (π/4 + x/2)
Solution:
Let us solve LHS,
= cos x/(1 – sin x)
As we know that,
cos 2x = cos2x – sin2x
cos x = cos2 x/2 – sin2 x/2
sin 2x = 2 sin x cos x
sin x = 2 sin x/2 cos x/2
So,
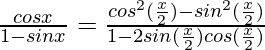
= ![Rendered by QuickLaTeX.com \frac{[cos(\frac{x}{2})-sin(\frac{x}{2})][cos(\frac{x}{2})+sin(\frac{x}{2})]}{sin^2(\frac{x}{2})+cos^2(\frac{x}{2})+2sin(\frac{x}{2})cos(\frac{x}{2})}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-18c03020729a4f5ee025e238fcb02ca3_l3.png)
By using the formulas,
a2 – b2 = (a – b)(a + b) and sin2x + cos2x = 1), we get
= ![Rendered by QuickLaTeX.com \frac{[cos(\frac{x}{2})-sin(\frac{x}{2})][cos(\frac{x}{2})+sin(\frac{x}{2})]}{[sin(\frac{x}{2})+cos(\frac{x}{2})]^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-457b250c0cd3b8c6b3e662a425a9dccb_l3.png)
= ![Rendered by QuickLaTeX.com \frac{[cos(\frac{x}{2})-sin(\frac{x}{2})][cos(\frac{x}{2})+sin(\frac{x}{2})]}{[sin(\frac{x}{2})+cos(\frac{x}{2})][sin(\frac{x}{2})+cos(\frac{x}{2})]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-863ffce0ad0292356d4acd70b74d921a_l3.png)
= 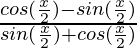
= 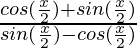
Now multiply numerator and denominator by 1/√2, we get,
= ![Rendered by QuickLaTeX.com \frac{\frac{1}{√2}[cos(\frac{x}{2})+sin(\frac{x}{2})]}{\frac{1}{√2}[sin(\frac{x}{2})-cos(\frac{x}{2})]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d4a0ad0e2bba8c67e1e0547194680501_l3.png)
= 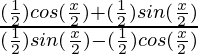
= 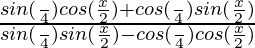
= 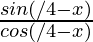
= tan (π/4 – x)
LHS = RHS
Hence proved.
Question 9. cos2 π/8 + cos2 3π/8 + cos2 5π/8 + cos2 7π/8 = 2
Solution:
Let us solve LHS,
= cos2 π/8 + cos2 3π/8 + cos2 5π/8 + cos2 7π/8
As we know that,
cos 2x = 2cos2x – 1
cos 2x+1=2cos2 x
cos2x = (Cos 2x + 1)/2
So,
= cos2 π/8 + cos2 3π/8 + cos2 5π/8 + cos2 7π/8
= 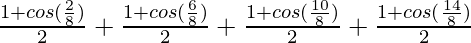
= 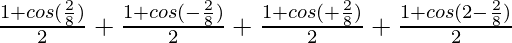
= 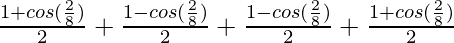
As we know that, cos (π – A) =- cos A, cos (π+ A) = -cos A and cos (2π – A) = cos A
= 2 x {1 + cos(2π/8)/2} + 2 x {1 – cos(2π/8)/2}
= 1 + cos(2π/8) + 1 – cos(2π/8)
= 2
LHS = RHS
Hence Proved.
Question 10. sin2 π/8 + sin2 3π/8 + sin2 5π/8 + sin2 7π/8
Solution:
Let us solve LHS,
= sin2 π/8 + sin2 3π/8 + sin2 5π/8 + sin2 7π/8
As we know that,
cos 2x = 1 – 2sin2x
2sin2x = 1 – cos 2x
sin2x = (1 – cos 2x)/2
So,
= 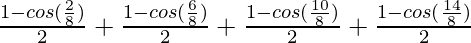
= 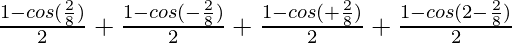
= 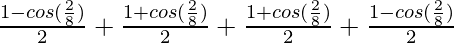
As we know, cos (π – A) = -cos A, cos (π + A) = -cos A and cos (2π – A) = cos A
= 2 x {1 – cos(2π/8)/2} + 2 x {1 + cos(2π/8)/2}
= 1 – cos(2π/8) + 1 + cos(2π/8)
= 2
LHS = RHS
Hence proved.
Question 11. (cos α + cos β)2 + (sin α + sin β)2 = 4 cos2(α – β)/2
Solution:
Let us solve LHS,
= (cos α+ cos β)2+ (sin α+ sin β)2
On expanding, we get,
= cos2α + cos2 β + 2 cos α cos β + sin2α+ sin2β + 2 sin α sin β
= 2+2 cos α cos β + 2 sin α sin β
= 2 (1+ cos α cos β+ sin α sin β)
= 2 (1 + cos (α – β)) [Using, cos (A – B) = cos A cos B+ sin A sin B]
= 2 (1 + 2 cos2(α – β)/2 – 1) [Using, cos2x = 2cos2x – 1]
= 2 (2 cos2(α – β)/2)
= 4 cos2(α – β)/2
LHS = RHS
Hence Proved.
Question 12. sin2(π/8 + x/2) – sin2(π/8 – x/2) = 1/√2 sin x
Solution:
Let us solve LHS,
= sin2(π/8 + x/2) – sin2(π/8 – x/2)
As we know that,
sin2A – sin2B = sin (A + B) sin (A-B)
So,
sin2(π/8 + x/2) – sin2(π/8 – x/2) = sin (π/8 + x/2 + π/8 – x/2) sin (π/8 + x/2 – (π/8 – x/2))
= sin (π/8 + π/8) sin (π/8 + x/2 – π/8 + x/2)
= sin π/4 sin x
= 1/√2 sin x [As we know that, π/4 = 1/√2]
LHS = RHS
Hence proved.
Question 13. 1 + cos22x = 2 (cos4x + sin4x)
Solution:
Let us solve LHS,
= 1 + cos22x
As we know that,
cos2x = cos2x sin2x
cos2x+ sin2x = 1
So,
1 + cos22x = (cos2x+ sin2x)2 + (cos2x – sin2x)2
= (cos4x + sin4x + 2 cos2x sin2x) + (cos4x + sin4x – 2cos2x sin2x)
= cos4x + sin4x + cos4x + sin4x
= 2 cos4x + 2 sin4x
= 2 (cos4x + sin4x)
LHS = RHS
Hence proved.
Question 14. cos32x + 3 cos 2x = 4 (cos6x – sin6x)
Solution:
Let us solve RHS,
= 4 (cos6 x – sin6 x)
On expanding, we get,
4 (cos6 x – sin6 x) = 4 [(cos2x)3 – (sin2x)3]
= 4 (cos2x – sin2x) (cos4x + sin4x + cos2x sin2x)
Now, using the formula, we get
a3 – b3 = (a – b) (a2 + b2 + ab)
= 4 cos 2x (cos4x + sin4x + cos2x sin2x + cos2x sin2x – cos2x sin2x
As we know that,
cos 2x = cos2x – sin2x
So,
= 4 cos 2x (cos4x + sin4x + 2 cos2x sin2x – cos2x sin2x)
= 4 cos 2x [(cos2x)2 + (sin2x)2 + 2 cos2x sin2x – cos2x sin2x]
By using formula,
a2 + b2 + 2ab = (a + b)2, we get
= 4 cos 2x [(1)2 – 1/4 (4 cos2 x sin2 x)]
= 4 cos 2x [(1)2-1/4 (2 cos x sin x)2]
Since
sin 2x = 2sin x cos x
= 4 cos 2x [(12) – 1/4 (sin 2x)2]
= 4 cos 2x (1 – 1/4 sin2 2x)
Since
sin2 x = 1 – cos2x
= 4 cos 2x [1 – 1/4 (1 – cos2 2x)]
= 4 cos 2x [1 – 1/4 + 1/4 cos2 2x]
= 4 cos 2x [3/4 + 1/4 cos2 2x]
= 4 (3/4 cos 2x + 1/4 cos³ 2x)
= 3 cos 2x + cos3 2x
= cos3 2x + 3 cos 2x
LHS = RHS
Hence proved.
Question 15. (sin 3A + sin A) sin A + (cos 3A – cos A) cos A = 0
Solution:
Let us solve LHS,
= (sin 3A + sin A) sin A + (cos 3A – cos A) cos A
= (sin 3A) (sin A) + sin2A + (cos 3A) (cos A) – cos2A
= [(sin 3A) (sin A) + (cos 3A) (cos A)] + (sin2A – cos2A)
= [(sin 3A) (sin A) + (cos 3A) (cos A)] – (cos2A – sin2A)
= cos (3A – A) – cos 2A
As we know that,
cos 2x = cos2A – sin2A
cos A cos B + sin A sin B = cos(A – B)
So,
= cos 2A – cos 2A
= 0
LHS = RHS
Hence Proved.
Share your thoughts in the comments
Please Login to comment...