Class 11 RD Sharma Solutions – Chapter 17 Combinations- Exercise 17.2 | Set 2
Last Updated :
30 Apr, 2021
Question 12. In an examination, a student to answer 4 questions out of 5 questions; questions 1 and 2 are however compulsory. Determine the number of ways in which the student can make a choice.
Solution:
Total number of questions = 5
Total number of questions to be answered = 4
As 2 questions are compulsory to answer, student can choose only 2 questions (4−2) out of the remaining 3 questions (5−2).
So, number of ways = 3C2
=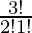
=
= 3
Therefore, the number of ways answering the questions is 3.
Question 13. A candidate is required to answer 7 questions out of 12 questions which are divided into two groups, each containing 6 questions. He is not permitted to attempt more than 5 questions from either group. In how many ways can he choose the 7 questions?
Solution:
Total number of questions = 12
Total number of questions to be answered = 7
Total number of questions in each set = 6
Now a student can’t attempt 5 questions from either group but has to answer 7 questions in total.
So, number of ways = (6C5 × 6C2) + (6C4 × 6C3) + (6C3 × 6C4) + (6C2 × 6C5)
=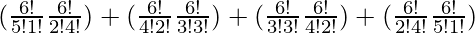
=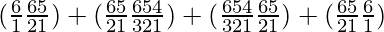
= (6×15) + (15×20) + (20×15) + (15×6)
= 90 + 300 + 300 + 90
= 780
Therefore, the number of ways of answering 7 questions is 780.
Question 14. There are 10 points in a plane of which 4 are collinear. How many different straight lines can be drawn by joining these points.
Solution:
Total number of points = 10
Number of collinear points = 4
Now we know, number of lines formed will be the difference between total number of lines formed by all 10 points and number of lines formed by collinear points added with 1.
Here, we add 1 because only 1 line can be formed by the given four collinear points.
So, number of ways = 10C2 – 4C2 + 1
=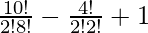
=
= 45 – 6 + 1
= 40
Therefore, the total number of ways of drawing different lines is 40.
Question 15. Find the number of diagonals of
(i) a hexagon
Solution:
A hexagon has 6 angular points. By joining any two angular points we get a line which is either a side or a diagonal.
So number of lines formed = 6C2
=
=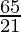
= 3×5
= 15
We know number of sides of hexagon is 6.
So, number of diagonals = 15 – 6 = 9
Therefore, the total number of diagonals of a hexagon is 9.
(ii) a polygon of 16 sides
Solution:
A polygon of 16 sides has 16 angular points. By joining any two angular points we get a line which is either a side or a diagonal.
So number of lines formed = 16C2
=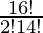
=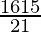
= 8×15
= 120
Number of sides of given polygon = 16
So, number of diagonals = 120 – 16 = 104
Therefore, the total number of diagonals of a hexagon is 104.
Question 16. How many triangles can be obtained by joining 12 points, five of which are collinear?
Solution:
We know that 3 points are required to draw a triangle.
Since 5 out of 12 points are collinear, so number of triangles that can be formed would be the difference between the number of triangles formed by all 12 points and the number of triangles formed by collinear points.
So, number of triangle= 12C3 – 5C3
=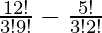
=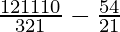
= (2×11×10) – (5×2)
= 220 – 10
= 210
Therefore, the total number of triangles that can be formed is 210.
Question 17. In how many ways can a committee of 5 persons be formed out of 6 men and 4 women when at least one women has to be necessarily selected?
Solution:
Total number of men = 6
Total number of women = 4
Total number of persons to be selected = 5.
Now it is given that we must choose at least one woman. It means we can choose from 1 to all 4 women in our committee at a time. Number of men will change according to it.
So, number of ways = (4C1 × 6C4) + (4C2 × 6C3) + (4C3 × 6C3) + (4C4 × 6C1)
=
=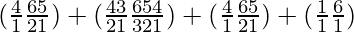
= 60 + 120 + 60 + 6
= 246
Therefore, the number of ways of selection is 246.
Question 18. In a village, there are 87 families of which 52 families have at most 2 children. In a rural development program, 20 families are to be helped chosen for assistance, of which 18 families must have at most 2 children. In how many ways can the choice be made?
Solution:
Its given that 52 families have at most 2 children out of 87. Therefore the remaining 35 families have exactly 2 children.
Now to choose any 20 families of which 18 families must have at most 2 children can be done in 3 ways. Either we can choose all the 20 families out of those 52 who have at most children, or 19 out of 52 and remaining 1 out of 35, or 18 families from 52 and remaining 2 out of 35.
So, total number of ways = (52C18 × 35C2) + (52C19 × 35C1) + (52C20 × 35C0)
Question 19. A group consists of 4 girls and 7 boys. In how many ways can a team of 5 members be selected if the team has
(i) no girls
(ii) at least one boy and girl
(iii) at least 3 girls
Solution:
Number of girls = 4
Number of boys = 7
Number of members to be selected = 5
(i) no girls
As it is given that the team cannot have a girl, we have to choose 5 members out of 7 boys.
So, number of ways = 7C5
=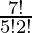
=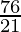
= 21
Therefore, the number of ways of selection such that team has no girls is 21.
(ii) at least one boy and girl
To select a team which consists of at least one boy and girl, we can choose from 1 to all the 4 girls at a time. Number of boys will change according to it.
So, number of ways = (7C1 × 4C4) + (7C2 × 4C3) + (7C3 × 4C3) + (7C4 × 4C1)
=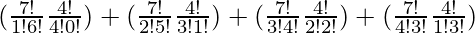
=
= 7+84+210+140
= 441
Therefore, the number of ways of selection such that team has at least one boy and girl is 441.
(iii) at least 3 girls
To select a team which consists of at least 3 girls, we can choose either 3 or 4 girls at a time. Number of boys will change according to it.
So, number of ways = (7C2 × 4C3) + (7C1 × 4C4)
=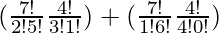
=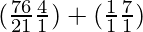
= 84 + 7
= 91
Therefore, the number of ways of selection such that team has at least 3 girls is 91.
Question 20. A committee of 3 persons is to be constituted from a group of 2 men and 3 women. In how many ways can this be done? How many of these committees would consist of 1 man and 2 women?
Solution:
Total number of men = 2
Total number of women = 3
So total number of persons = 2+3 = 5
Number of persons to be selected = 3
It is given that a committee of 3 persons has to be formed. So we have to choose 3 persons from 5 persons.
So, number of ways = 5C3
=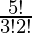
=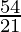
= 10
Also we have to find the number of committees consisting of 1 man and 2 women. So we have to choose 1 man out of 2 men and 2 women out of 3 women.
So, number of ways = 2C1 × 3C2
=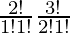
= 6
Question 21. Find the number of
(i) diagonals formed in a decagon.
Solution:
A decagon has 10 sides. By joining any two angular points we get a line which is either a side or a diagonal.
So number of lines formed = 10C2
=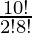
=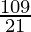
= 45
Number of sides = 10
So, number of diagonals = 45−10 = 35.
Therefore, number of diagonals formed in a decagon is 35.
(ii) triangles formed in a decagon.
Solution:
A decagon has 10 sides. By joining any 3 angular points we get a triangle.
So number of lines formed = 10C3
=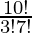
=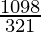
=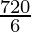
= 120
Therefore, number of triangles formed in a decagon is 120.
Question 22. Determine the number of 5 cards combinations out of a deck of 52 cards if at least one of the 5 cards has to be a king?
Solution:
Out of a deck of 52 cards, we have to choose 5 cards combinations where at least one of the 5 cards has to be a king.
We know there are 4 kings in a deck of 52 cards. So, we can choose from 1 to all the four kings at a time and selection of remaining cards will change accordingly.
So, number of ways = (4C1 × 48C4) + (4C2 × 48C3) + (4C3 × 48C2) + (4C4 × 48C1)
=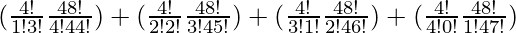
=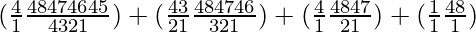
= 778320 + 103776 + 4512 + 48
= 886656
Therefore, number of ways of selecting 5 card combinations if at least one of the 5 cards has to be a king is 886656.
Share your thoughts in the comments
Please Login to comment...