In mathematics, a function(e.g. f), is said to be an inverse of another(e.g. g), if given the output of g returns the input value given to f. Additionally, this must hold true for every element in the domain co-domain(range) of g. E.g. assuming x and y are constants if g(x) = y and f(y) = x then the function f is said to be an inverse of the function g. Or in other words, if a function f : A ⇢ B is one – one and onto function or bijective function, then a function defined by g : B ⇢ A is known as inverse of function f. The inverse function is also known as the anti function. The inverse of function is denoted by f-1.
f(g(x)) = g(f(x)) = x
Here, f and g are inverse functions.
Procedure of finding inverse of f:
- Check for one-one and onto function.
- If invertible then, interchange x and y in definition of f(x).
- Find y in terms of x.
- Obtained y is inverse of f defined from B ⇢ A.
Example: f(x) = ex
y = ex
Inverse of f(x) will be obtained by y ↔ x
x = ey
y = ln x
Now, ex and ln x are inverse function of each other.

Inverse functions ex and ln x are symmetry about y = x.
Derivatives of inverse functions
As we already know that what is inverse function, so now we are going to find the derivative of inverse function. So, if a function f(x) is a continuous one-to-one function or bijective function defined on an interval lets say I, then its inverse is also continuous and if the function f(x) is a differentiable function, then its inverse is also a differentiable function.
g'(x) = 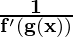
Here, f and g are inverse function. It is known as inverse function theorem.
Proof:
Let us considered f and g be the inverse functions and x is present in the g domain, then
f(g(x)) = x
Differentiate both side with respect to x
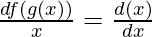
Now solve the LHS using chain rule we get
f'(g(x))g'(x) = 1
Now solve for g'(x):
g'(x) = 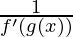
Hence, the derivative on inverse function is solved.
Example 1: f(x) = ex, check whether condition holds true. Solution:
As, f(x) = ex
y = ex
x = ln y
g(x) = f-1(x) = ln x
Now,
f'(x) = 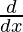 (ex) = ex
(ex) = ex
g'(x) = 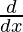 (ln x) =
(ln x) = 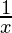
g'(f(x)) = 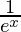
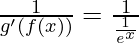 = ex
= ex
Hence,
f'(x) = 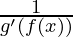 , holds true.
, holds true.
Example 2: Let f(x) = 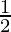 x3 + 3x – 4, and let g be the inverse function of f where f(-2) = -14. Find g'(-14) Solution:
x3 + 3x – 4, and let g be the inverse function of f where f(-2) = -14. Find g'(-14) Solution:
f'(x) = 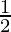 (3x2) + 3
(3x2) + 3
According to eq(1).
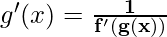
As, f(x) = g-1(x) and f(-2) = -14
then g(-14) = -2
x = -14
g'(-14) = 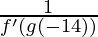
g'(-14) = 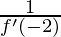
f'(-2) = 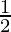 (3(-2)2) + 3
(3(-2)2) + 3
f'(-2) = 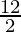 + 3
+ 3
f'(-2) = 9
then, g'(-14) = 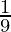
How to find derivatives of inverse functions from the table?
Let us discuss this concept with the help of an example. So let us assume g and f be the inverse function and the following table lists a few values of f, g and f’.
| x | f(x) | g(x) | f'(x) |
|---|
| 2 | 4 | 8 | 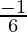 |
| 8 | 3 | 2 | 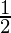 |
We have to find g'(2). As it said from the question, that f and g be inverse functions. This means if we have two sets, now let us assume that the first set is the domain of f. So in this set, if we start from some x value then f is going to map that x to another value which is known as f(x)(this is the use of function f). Now as we know that g is the inverse of f, so this g gets us back to the first set(this is the use of function g).

Hence we get
g(f(x)) = x …(i)
f(g(x)) = x …(ii)
Where, both are valid.
From eq(ii), we have
f(g(x)) = x
Now differentiate both side w.r.t. x. we get
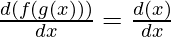
Now on the LHS we apply chain rule, now we get
f'(g(x))g'(x) = 1
g'(x) = 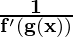
Now we are going to find the value of g'(2)
g'(2) = 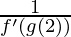
From the table we get the value of g(2)
g'(2) = 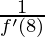
From the table we get the value of f'(8)
g'(2) = 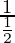
g'(2) = 2
Hence, the value of g'(2) = 2.
How to find the derivatives of inverse trigonometric functions?
We remark that inverse trigonometric functions are continuous functions. Now we use first principles and chain rule to find derivatives of these functions:
1. Derivative of f given by f(x) = sin–1 x.
From first principle
f(x) = sin–1 x and f(x+h) = sin–1 (x+h)
![Rendered by QuickLaTeX.com \frac{d}{dx}(f(x)) = \lim_{h\to0} \frac{f(x+h)-f(x)}{h} \\ = \lim_{h\to0} \frac{sin^{-1}(x+h)-sin^{-1}x}{h}\\ = \lim_{h\to0} \frac{sin^{-1}[(x+h)\sqrt{1-x^2} - x\sqrt{1-(x+h)^2}]}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-88881d095cc2b808df719491954bdf7f_l3.png)
Using the formula,
sin–1 x – sin–1 y = sin-1(x 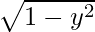 – y
– y 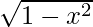 )
)
![Rendered by QuickLaTeX.com = \lim_{h\to0} \frac{sin^{-1}[(x+h)\sqrt{1-x^2}-x\sqrt{1-(x+h)^2}]}{(x+h)\sqrt{1-x^2}-x\sqrt{1-(x+h)^2}} \times \frac{(x+h)\sqrt{1-x^2}-x\sqrt{1-(x+h)^2}}{h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-18fab7a0f652b31f617550df9ad917a5_l3.png)
As
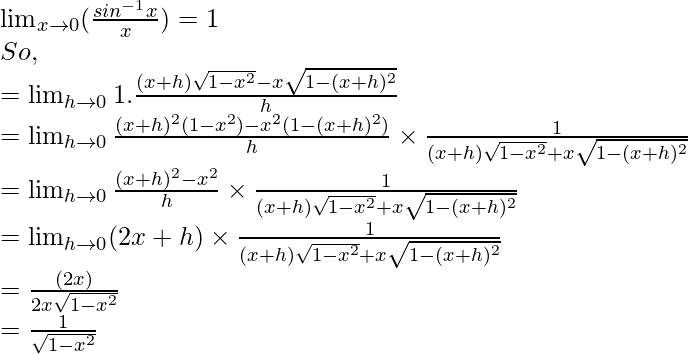
Hence
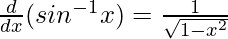
From chain rule
y = sin-1x
sin y = x
Differentiating both sides w.r.t x, we get
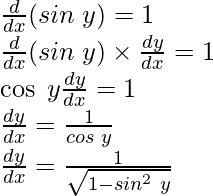
As
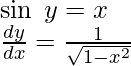
2. Derivative of f given by f(x) = cos–1 x.
From first principle
f(x) = cos–1 x and f(x+h) = cos–1 (x+h)
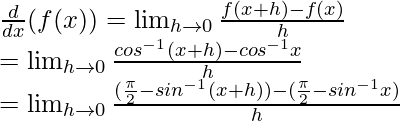
As
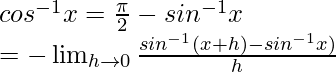
By using the previous result
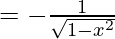
Hence,
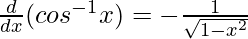
From chain rule
y = cos-1x
cos y = x
Differentiating both sides w.r.t x, we get

As
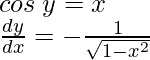
3. Derivative of f given by f(x) = tan–1 x.
From first principle
f(x) = tan–1 x and f(x+h) = tan–1 (x+h)
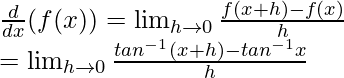
As
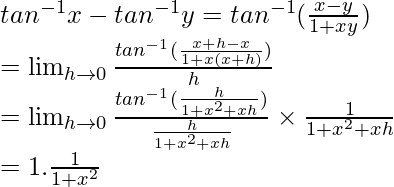
Hence
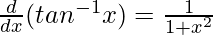
From chain rule
y = tan-1x
tan y = x
Differentiating both sides w.r.t x, we get
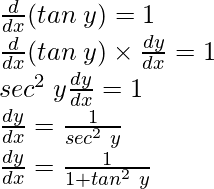
As
tan y = x dy/dx = 1/1+x2
4. Derivative of f given by f(x) = cot–1 x.
From first principle
f(x) = cot–1 x and f(x+h) = cot–1 (x+h)
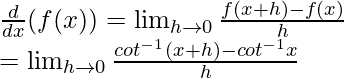
As
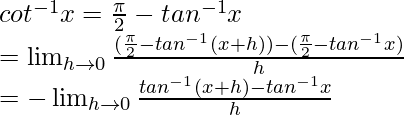
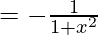
Hence
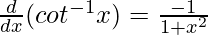
From chain rule
y = cot-1x
cot y = x
Differentiating both sides w.r.t x, we get
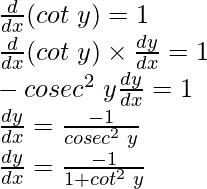
As
cot y = x dy/dx = -1/1 + x2
5. Derivative of f given by f(x) = sec–1 x.
From chain rule
y = sec-1x
sec y = x
Differentiating both sides w.r.t x, we get
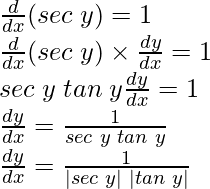
If x > 1, then y ∈ (0, π/2)
∴ sec y > 0, tan y > 0 ⇒ |sec y||tan y| = sec y tan y
If x < -1, then y ∈ (π/2,π)
∴ sec y < 0, tan y < 0 ⇒ |sec y||tan y| = (-sec y) (-tan y) = sec y tan y
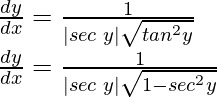
As
sec y = x
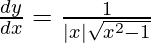
6. Derivative of f given by f(x) = cosec–1 x.
From chain rule
y = cosec-1x
cosec y = x
Differentiating both sides w.r.t x, we get
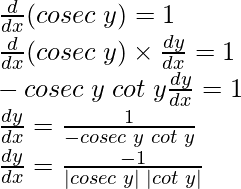
If x > 1, then y ∈ (0, π/2)
∴ cosec y > 0, cot y > 0 ⇒ |cosec y||cot y| = cosec y cot y
If x < -1, then y∈ (-π/2, 0)
∴ cosec y < 0, cot y < 0 ⇒ |cosec y||cot y| = (-cosec y) (-cot y)
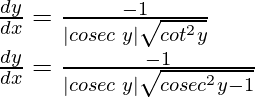
As
cosec y = x
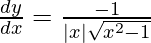
Examples:
Question 1. Find the derivative of y = tan -1 (x2).
Solution:
Differentiating both side, we get
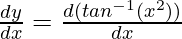
Using the inverse derivative of tan-1 θ
= 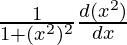
= 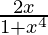
Question 2. Find the derivative of y = sin -1 (3x-2).
Solution:
Differentiating both side, we get
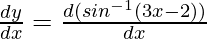
Using the inverse derivative of sin-1 θ
= 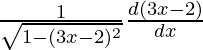
= 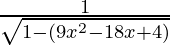 (3)
(3)
= 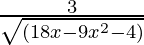
Question 3. Find the derivative of y = cos -1 (1 – x2).
Solution:
Differentiating both side, we get
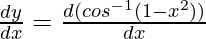
Using the inverse derivative of cos-1 θ
= 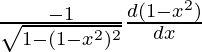
= 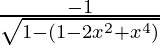 (-2x)
(-2x)
= 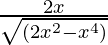
= 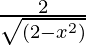
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...