In each of the following Exercise 1 to 5, find the equation of the circle with
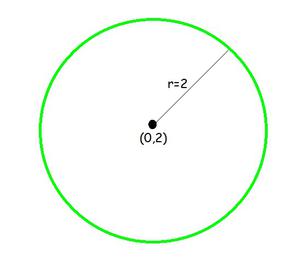
Question 1: Centre (0, 2) and radius 2
Solution:
Given: Centre (0, 2) and radius (r) = 2
The equation of a circle with centre as (h, k) and radius as r is given as (x – h)2 + (y – k)2 = r2
As, Centre (h, k) = (0, 2) and radius (r) = 2
Thus, the equation of the circle is
(x – 0)2 + (y – 2)2 = 22 [by using formula (a – b)2 = a2 – 2ab + b2]
x2 + y2 + 4 – 4y = 4
x2 + y2 – 4y = 0
Therefore, the equation of the circle is x2 + y2 – 4y = 0
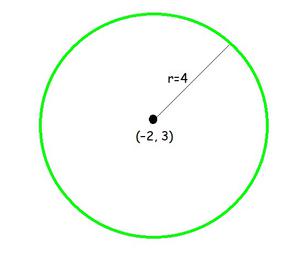
Question 2: Centre (–2, 3) and radius 4
Solution:
Given: Centre (-2, 3) and radius (r) = 4
The equation of a circle with centre as (h, k) and radius as r is given as (x – h)2 + (y – k)2 = r2
As, centre (h, k) = (-2, 3) and radius (r) = 4
Thus, the equation of the circle is
(x + 2)2 + (y – 3)2 = (4)2 [by using formula (a – b)2 = a2 – 2ab + b2]
x2 + 4x + 4 + y2 – 6y + 9 = 16
x2 + y2 + 4x – 6y – 3 = 0
Therefore, the equation of the circle is x2 + y2 + 4x – 6y – 3 = 0
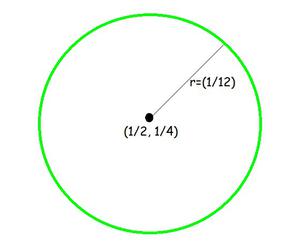
Question 3: Centre (1/2, 1/4) and radius (1/12)
Solution:
Given: Centre (1/2, 1/4) and radius 1/12
The equation of a circle with centre as (h, k) and radius as r is given as (x – h)2 + (y – k)2 = r2
So, centre (h, k) = (1/2, 1/4) and radius (r) = 1/12
Thus, the equation of the circle is
(x – 1/2)2 + (y – 1/4)2 = (1/12)2 [by using formula (a – b)2 = a2 – 2ab + b2]
x2 – x + 1/4 + y2 – y/2 + 1/16 = 1/144
x2 – x + 1/4 + y2 – y/2 + 1/16 = 1/144
144x2 – 144x + 36 + 144y2 – 72y + 9 – 1 = 0
144x2 – 144x + 144y2 – 72y + 44 = 0
36x2 + 36x + 36y2 – 18y + 11 = 0
36x2 + 36y2 – 36x – 18y + 11= 0
Therefore, the equation of the circle is 36x2 + 36y2 – 36x – 18y + 11= 0
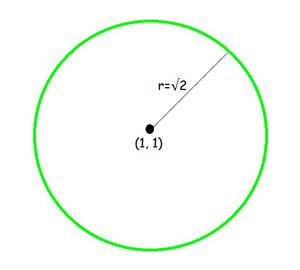
Question 4: Centre (1, 1) and radius √2
Solution:
Given: Centre (1, 1) and radius √2
The equation of a circle with centre as (h, k) and radius as r is given as (x – h)2 + (y – k)2 = r2
So, centre (h, k) = (1, 1) and radius (r) = √2
Thus, the equation of the circle is
(x-1)2 + (y-1)2 = (√2)2 [by using formula (a – b)2 = a2 – 2ab + b2]
x2 – 2x + 1 + y2 -2y + 1 = 2
x2 + y2 – 2x -2y = 0
Therefore, the equation of the circle is x2 + y2 – 2x -2y = 0
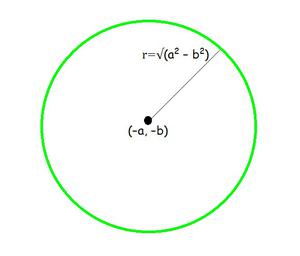
Question 5: Centre (–a, –b) and radius √(a2 – b2)
Solution:
Given: Centre (-a, -b) and radius √(a2 – b2)
The equation of a circle with centre as (h, k) and radius as r is given as (x – h)2 + (y – k)2 = r2
So, centre (h, k) = (-a, -b) and radius (r) = √(a2 – b2)
Thus, the equation of the circle is
(x + a)2 + (y + b)2 = (√(a2 – b2)2) [by using formula (a + b)2 = a2 + 2ab + b2]
x2 + 2ax + a2 + y2 + 2by + b2 = a2 – b2
x2 + y2 +2ax + 2by + 2b2 = 0
Therefore, the equation of the circle is x2 + y2 +2ax + 2by + 2b2 = 0
In each of the following Exercise 6 to 9, find the centre and radius of the circles.
Question 6: (x + 5)2 + (y – 3)2 = 36
Solution:
Given equation: (x + 5)2 + (y – 3)2 = 36
(x – (-5))2 + (y – 3)2 = 62
The equation is of the form (x – h)2 + (y – k)2 = r2 where, h = -5, k = 3 and r = 6
Therefore, the centre is (-5, 3) and its radius is 6.
Question 7: x2 + y2 – 4x – 8y – 45 = 0
Solution:
Given equation: x2 + y2 – 4x – 8y – 45 = 0.
x2 + y2 – 4x – 8y – 45 = 0
(x2 – 4x) + (y2 -8y) = 45
(x2 – 2(x) (2) + 22) + (y2 – 2(y) (4) + 42) – 4 – 16 = 45
(x – 2)2 + (y – 4)2 = 65
(x – 2)2 + (y – 4)2 = (√65)2
The equation is of the form (x-h)2 +(y-k)2 = r2 ,where h = 2, k = 4 and r = √65
Therefore, the centre is (2, 4) and its radius is √65.
Question 8: x2 + y2 – 8x + 10y – 12 = 0
Solution:
Given equation: x2 + y2 -8x + 10y -12 = 0.
x2 + y2 – 8x + 10y – 12 = 0
(x2 – 8x) + (y2 + 10y) = 12
(x2 – 2(x) (4) + 42) + (y2 – 2(y) (5) + 52) – 16 – 25 = 12
(x – 4)2 + (y + 5)2 = 53
(x – 4)2 + (y – (-5))2 = (√53)2
The equation is of the form (x-h)2 +(y-k)2 = r2 ,where h = 4, k= -5 and r = √53
Therefore, the centre is (4, -5) and its radius is √53.
Question 9: 2x2 + 2y2 – x = 0
Solution:
Given equation: 2x2 + 2y2 – x = 0.
2x2 + 2y2 – x = 0
(2x2 – x) + 2y2 = 0
(x2 – 2 (x) (1/4) + (1/4)2) + y2 – (1/4)2 = 0
(x – 1/4)2 + (y – 0)2 = (1/4)2
The equation is of the form (x-h)2 +(y-k)2 = r2, where, h = 1/4, k = 0, and r = 1/4
Therefore, the centre is (1/4, 0) and its radius is 1/4.
Question 10: Find the equation of the circle passing through the points (4,1) and (6,5) and whose centre is on the line 4x + y = 16.
Solution:
The equation of the circle is (x – h)2+ (y – k)2 = r2
As the circle passes through points (4,1) and (6,5)
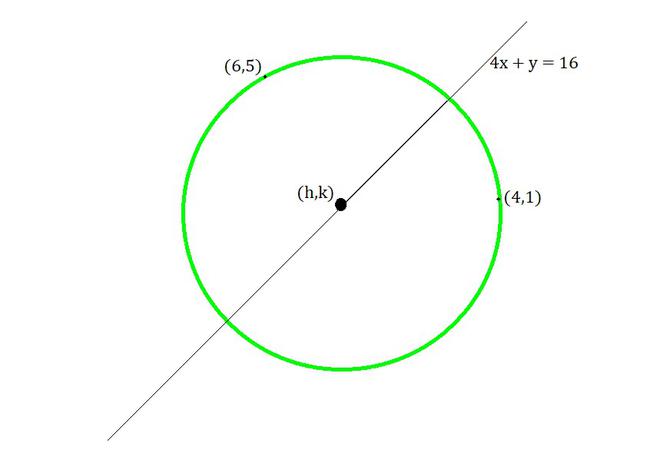
So, When the circle passes through (4,1)
(4 – h)2 + (1 – k)2 = r2 ……………..(1)
When the circle passes through (6,5)
(6 – h)2+ (5 – k)2 = r2 ………………(2)
Given that, the centre (h, k) of the circle lies on line 4x + y = 16,
4h + k =16 ………………… (3)
From equation (1) and (2), we get
(4 – h)2+ (1 – k)2 =(6 – h)2 + (5 – k)2
16 – 8h + h2 +1 -2k +k2 = 36 -12h +h2+15 – 10k + k2
16 – 8h +1 -2k + 12h -25 -10k
4h +8k = 44
h + 2k = 11 ……………. (4)
Now let us multiply equation (3) by 2, and subtracting it with equation (4), we get
(h + 2k) – 2(4h + k) = 11 – 32
h + 2k – 8h – 2k = -21
-7h = -21
h = 3
Substitute this value of h in equation (4), we get
3 + 2k = 11
2k = 11 – 3
2k = 8
k = 4
We get h = 3 and k = 4
When we substitute the values of h and k in equation (1), we get
(4 – 3)2+ (1 – 4)2 = r2
(1)2 + (-3)2 = r2
1+9 = r2
r = √10
Now, the equation of the circle is,
(x – 3)2 + (y – 4)2 = (√10)2
x2 – 6x + 9 + y2 – 8y + 16 =10
x2 + y2 – 6x – 8y + 15 = 0
Therefore, the equation of the circle is x2 + y2 – 6x – 8y + 15 = 0
Question 11: Find the equation of the circle passing through the points (2, 3) and (–1, 1) and whose centre is on the line x – 3y – 11 = 0.
Solution:
The equation of the circle is (x – h)2 + (y – k)2 = r2
As the circle passes through points (2,3) and (-1,1)
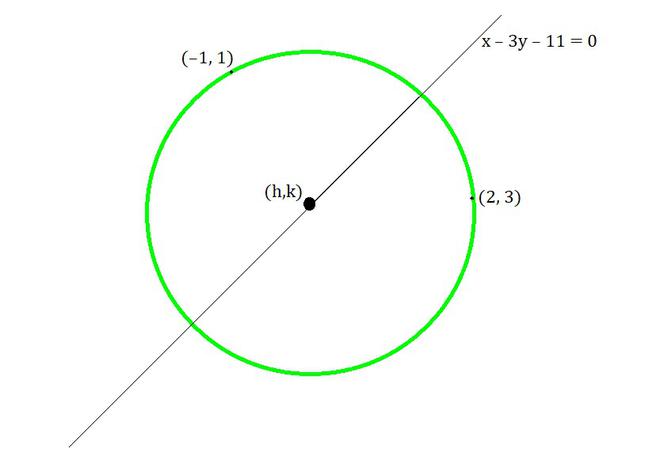
So, When the circle passes through (2,3)
(2 – h)2+ (3 – k)2 =r2 ……………..(1)
When the circle passes through (-1,1)
(-1 – h)2+ (1– k)2 =r2 ………………(2)
Given that, the centre (h, k) of the circle lies on line x – 3y – 11= 0,
h – 3k =11 ………………… (3)
From the equation (1) and (2), we get
(2 – h)2+ (3 – k)2 =(-1 – h)2 + (1 – k)2
4 – 4h + h2 +9 -6k +k2 = 1 + 2h +h2+1 – 2k + k2
4 – 4h +9 -6k = 1 + 2h + 1 -2k
6h + 4k =11 ……………. (4)
Now let us multiply equation (3) by 6, and subtracting it with equation 4, we get
6h+ 4k – 6(h-3k) = 11 – 66
6h + 4k – 6h + 18k = 11 – 66
22 k = – 55
k = -5/2
Substitute this value of k in equation (4), we get
6h + 4(-5/2) = 11
6h – 10 = 11
6h = 21
h = 21/6
h = 7/2
We get h = 7/2 and k = -5/2
On substituting the values of h and k in equation (1), we get
(2 – 7/2)2 + (3 + 5/2)2 = r2
[(4-7)/2]2 + [(6+5)/2]2 = r2
(-3/2)2 + (11/2)2 = r2
9/4 + 121/4 = r2
130/4 = r2
Now, the equation of the circle is,
(x – 7/2)2 + (y + 5/2)2 = 130/4
[(2x-7)/2]2 + [(2y+5)/2]2 = 130/4
4×2 -28x + 49 +4y2 + 20y + 25 =130
4x2 +4y2 -28x + 20y – 56 = 0
4(x2 +y2 -7x + 5y – 14) = 0
x2 + y2 – 7x + 5y – 14 = 0
Therefore, the equation of the circle is x2 + y2 – 7x + 5y – 14 = 0
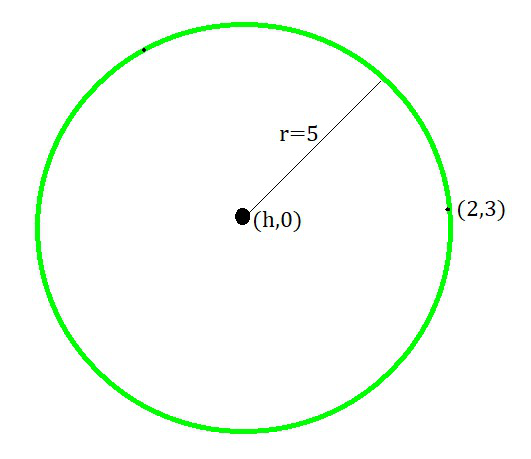
Question 12: Find the equation of the circle with radius 5 whose centre lies on x-axis and passes through the point (2, 3).
Solution:
The equation of the circle is (x – h)2+ (y – k)2 = r2
Given the radius of the circle is 5 and it’s centre lies on the x-axis, k = 0 and r = 5.
So now, the equation of the circle is (x – h)2 + y2 = 25.
Also given that the circle passes through the point (2, 3).
Therefore,
(2 – h)2+ 32 = 25
(2 – h)2 = 25-9
(2 – h)2 = 16
2 – h = ± √16 = ± 4
If 2-h = 4, then h = -2
If 2-h = -4, then h = 6
Now, when h = -2, the equation of the circle is
(x + 2)2 + y2 = 25
x2 + 4x + 4 + y2 = 25
x2 + y2 + 4x – 21 = 0
Now, when h = 6, the equation of the circle is
(x – 6)2 + y2 = 25
x2 -12x + 36 + y2 = 25
x2 + y2 -12x + 11 = 0
Therefore, the equation of the circle is x2 + y2 – 4x + 21 = 0 and x2 + y2 -12x + 11 = 0
Question 13: Find the equation of the circle passing through (0,0) and making intercepts a and b on the coordinate axes.
Solution:
The equation of the circle is (x – h)2+ (y – k)2 = r2
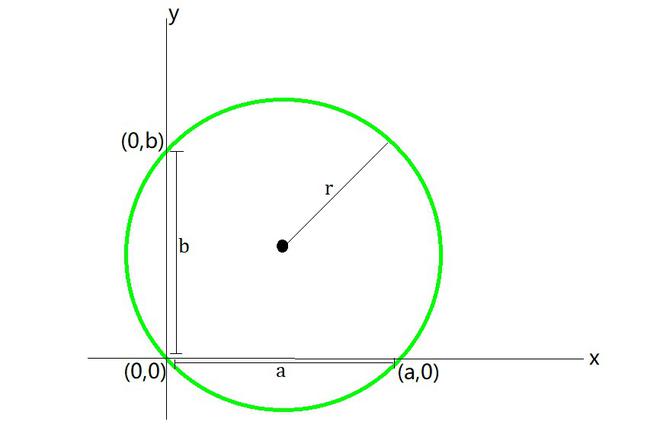
When the circle passes through (0, 0),we get,
(0 – h)2+ (0 – k)2 = r2
h2 + k2 = r2
The equation of the circle is (x – h)2 + (y – k)2 = h2 + k2.
Given that the circle intercepts points a and b on the coordinate axes.
Since, the circle passes through points (a, 0) and (0, b).
So the equations are,
(a – h)2+ (0 – k)2 = h2 +k2 ……………..(1)
(0 – h)2+ (b– k)2 = h2 +k2 ………………(2)
From equation (1), we get
a2 – 2ah + h2 + k2 = h2 + k2
a2 – 2ah = 0
a(a – 2h) =0
a = 0 or (a -2h) = 0
As, a ≠ 0; hence, (a -2h) = 0
h = a/2
From equation (2), we get
h2 – 2bk + k2 + b2 = h2 + k2
b2 – 2bk = 0
b(b– 2k) = 0
b= 0 or (b-2k) =0
As, a ≠ 0; hence, (b -2k) = 0
k = b/2
Now, substituting the value of h and k, we get
(x – a/2)2 + (y – b/4)2 = (a/2)2 + (b/2)2
[(2x-a)/2]2 + [(2y+b)/2]2 = (a2 + b2)/4
4x2 – 4ax + a2 +4y2 – 4by + b2 = a2 + b2
4x2 + 4y2 -4ax – 4by = 0
4(x2 +y2 -7x + 5y – 14) = 0
x2 + y2 – ax – by = 0
Therefore, the equation of the circle is x2 + y2 – ax – by = 0
Question 14: Find the equation of a circle with centre (2,2) and passes through the point (4,5).
Solution:
Given the centre of the circle as (h, k) = (2,2)
Also given that the circle passes through the point (4,5),
the radius (r) of the circle is the distance between the points (2,2) and (4,5).
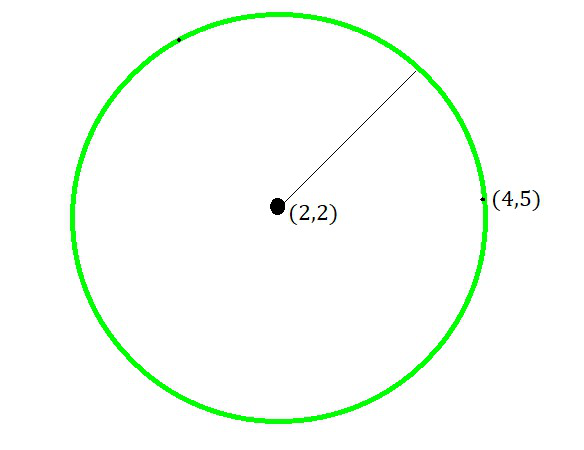
r = √[(2-4)2 + (2-5)2]
= √[(-2)2 + (-3)2]
= √[4+9]
= √13
Now, the equation of the circle is
(x– h)2+ (y – k)2 = r2
(x –h)2 + (y – k)2 = (√13)2
(x –2)2 + (y – 2)2 = (√13)2
x2 – 4x + 4 + y2 – 4y + 4 = 13
x2 + y2 – 4x – 4y = 5
Therefore, the equation of the circle is x2 + y2 – 4x – 4y = 5
Question 15: Does the point (–2.5, 3.5) lie inside, outside or on the circle x2 + y2 = 25?
Solution:
Given equation of the circle is x2 +y2 = 25.
x2 + y2 = 25
(x – 0)2 + (y – 0)2 = 52
The equation is of the form (x – h)2 + (y – k)2 = r2 ,where, h = 0, k = 0 and r = 5.
Now the distance between the point (-2.5, 3.5) and the centre (0,0) is
= √[(-2.5 – 0)2 + (-3.5 – 0)2]
= √(6.25 + 12.25)
= √18.5
= 4.3 [which is < 5]
Since, the distance between the point (-2.5, -3.5) and the centre (0, 0) of the circle is less than the radius of the circle.
Therefore, the point (-2.5, -3.5) lies inside the circle.
Share your thoughts in the comments
Please Login to comment...