Question 1. If a, b, c are in G.P., prove that log a, log b, log c are in A.P.
Solution:
Given: a, b and c are in G.P.
Using property of geometric mean, we get
b2 = ac
(b2)n = (ac)n
b2n = an cn
Now, use log on both the sides, we get,
log b2n = log (ancn)
log (bn)2 = log an + log cn
2 log bn = log an + log cn
Hence, proved log an, log bn, log cn are in A.P
Question 2. If a, b, c are in G.P., prove that 1/loga m, 1/logb m, 1/logc m are in A.P.
Solution:
Given: a, b and c are in GP
Using the property of geometric mean
b2 = ac
On applying log on both sides with base m, we get
logm b2 = logm ac
Using property of log
logm b2 = logm a + logm c
2logm b = logm a + logm c
2/logb m = 1/loga m + 1/logc m
Hence, proved 1/loga m, 1/logb m, 1/logc m are in A.P.
Question 3. Find k such that k + 9, k – 6, and 4 forms three consecutive terms of a G.P.
Solution:
Let us considered
a = k + 9
b = k − 6
c = 4
AS we know that a, b and c are in GP, then
By using property of geometric mean, we get
b2 = ac
(k − 6)2 = 4(k + 9)
k2 – 12k + 36 = 4k + 36
k2 – 16k = 0
k = 0 or k = 16
Question 4. Three numbers are in A.P., and their sum is 15. If 1, 3, 9 be added to them respectively, they form a G.P. find the numbers.
Solution:
Let us considered the first term of an A.P. = a
Common difference = d
a1 + a2 + a3 = 15
Here, the three number are: a, a + d, and a + 2d
So,
a + a + d + a + 2d = 15
3a + 3d = 15 or a + d = 5
d = 5 – a -(1)
a + 1, a + d + 3, and a + 2d + 9
They are in GP, that is:
(a + d + 3)/(a + 1) = (a + 2d + 9)/(a + d + 3)
(a + d + 3)2 = (a + 2d + 9)(a + 1)
a2 + d2 + 9 + 2ad + 6d + 6a = a2 + a + 2da + 2d + 9a + 9
(5 – a)2 – 4a + 4(5 – a) = 0
25 + a2 – 10a – 4a + 20 – 4a = 0
a2 – 18a + 45 = 0
a2 – 15a – 3a + 45 = 0
a(a – 15) – 3(a – 15) = 0
a = 3 or a = 15
d = 5 – a
d = 5 – 3 or d = 5 – 15
d = 2 or – 10
Then,
For a = 3 and d = 2, A.P is 3, 5, 7
For a = 15 and d = -10, A.P is 15, 5, -5
Hence, the numbers are 3, 5, 7 or 15, 5, – 5
Question 5. The sum of three numbers which are consecutive terms of an A.P. is 21. If the second number is reduced by 1 and the third is increased by 1, we obtain three consecutive terms of a G.P. Find the numbers.
Solution:
Let us considered the first term of an A.P. be = a
Common difference = d
a1 + a2 + a3 = 21
Here, the three number are: a, a + d, and a + 2d
So,
3a + 3d = 21 or
a + d = 7.
d = 7 – a -(1)
a, a + d – 1, and a + 2d + 1
They are now in GP, that is:
(a + d – 1)/a = (a + 2d + 1)/(a + d – 1)
(a + d – 1)2 = a(a + 2d + 1)
a2 + d2 + 1 + 2ad – 2d – 2a = a2 + a + 2da
(7 – a)2 – 3a + 1 – 2(7 – a) = 0
49 + a2 – 14a – 3a + 1 – 14 + 2a = 0
a2 – 15a + 36 = 0
a2 – 12a – 3a + 36 = 0
a(a – 12) – 3(a – 12) = 0
a = 3 or a = 12
d = 7 – a
d = 7 – 3 or d = 7 – 12
d = 4 or – 5
Then,
For a = 3 and d = 4, A.P is 3, 7, 11
For a = 12 and d = -5, A.P is 12, 7, 2
Hence, the numbers are 3, 7, 11 or 12, 7, 2
Question 6. The sum of three numbers a, b, c in A.P. is 18. If a and b are each increased by 4 and c is increased by 36, the new numbers form a G.P. Find a, b, c.
Solution:
Let us considered the first term of an A.P. = a
Common difference = d
b = a + d; c = a + 2d.
Given:
a + b + c = 18
3a + 3d = 18 or a + d = 6.
d = 6 – a -(1)
a + 4, a + d + 4, and a + 2d + 36
They are now in GP, that is:
(a + d + 4)/(a + 4) = (a + 2d + 36)/(a + d + 4)
(a + d + 4)2 = (a + 2d + 36)(a + 4)
a2 + d2 + 16 + 8a + 2ad + 8d = a2 + 4a + 2da + 36a + 144 + 8d
d2 – 32a – 128
(6 – a)2 – 32a – 128 = 0
36 + a2 – 12a – 32a – 128 = 0
a2 – 44a – 92 = 0
a2 – 46a + 2a – 92 = 0
a(a – 46) + 2(a – 46) = 0
a = – 2 or a = 46
d = 6 –a
d = 6 – (– 2) or d = 6 – 46
d = 8 or – 40
Then,
For a = -2 and d = 8, A.P is -2, 6, 14
For a = 46 and d = -40, A.P is 46, 6, -34
Hence, the numbers are – 2, 6, 14 or 46, 6, – 34
Question 7. The sum of three numbers in G.P. is 56. If we subtract 1, 7, 21 from these numbers in that order, we obtain an A.P. Find the numbers.
Solution:
Let us considered the three numbers = a, ar, ar2
a + ar + ar2 = 56 -(1)
Now, subtract 1, 7, 21 from the numbers, we get,
(a – 1), (ar – 7), (ar2 – 21)
The above numbers are in AP.
If three numbers are in AP,
So, according to the arithmetic mean, we can write as 2b = a + c
2 (ar – 7) = a – 1 + ar2 – 21
= (ar2 + a) – 22
2ar – 14 = (56 – ar) – 22
2ar – 14 = 34 – ar
3ar = 48
ar = 48/3
ar = 16
a = 16/r -(2)
Now, substitute the value of a in eq(1) we get,
(16 + 16r + 16r2)/r = 56
16 + 16r + 16r2 = 56r
16r2 – 40r + 16 = 0
2r2 – 5r + 2 = 0
2r2 – 4r – r + 2 = 0
2r(r – 2) – 1(r – 2) = 0
(r – 2) (2r – 1) = 0
r = 2 or 1/2
Substitute the value of r in eq(2) we get,
a = 16/r
= 16/2 or 16/(1/2)
= 8 or 32
Hence, the three numbers are (a, ar, ar2) is (8, 16, 32)
Question 8. if a, b, c are in G.P., prove that:
(i) a(b2 + c2) = c(a2 + b2)
(ii) a2b2c2 [1/a3 + 1/b3 + 1/c3] = a3 + b3 + c3
(iii) (a+b+c)2 / (a2 + b2 + c2) = (a+b+c) / (a-b+c)
(iv) 1/(a2 – b2) + 1/b2 = 1/(b2 – c2)
(v) (a + 2b + 2c) (a – 2b + 2c) = a2 + 4c2
Solution:
(i) Given: a, b, c are in GP.
Using the property of geometric mean,
b2 = ac
Let LHS: a(b2 + c2)
Now, on substituting b2 = ac, we get
a(ac + c2)
a2c + ac2
c(a2 + ac)
On Substituting ac = b2 we get,
c(a2 + b2) = RHS
LHS = RHS
Hence, proved.
(ii) Given: a, b, c are in GP.
Using the property of geometric mean,
b2 = ac
Let LHS: a2b2c2 [1/a3 + 1/b3 + 1/c3]
a2b2c2/a3 + a2b2c2/b3 + a2b2c2/c3
b2c2/a + a2c2/b + a2b2/c
(ac)c2/a + (b2)2/b + a2(ac)/c -(∵ b2 = ac)
ac3/a + b4/b + a3c/c
c3 + b3 + a3 = RHS
LHS = RHS
Hence, proved.
(iii) Given: a, b, c are in GP.
Using the property of geometric mean,
b2 = ac
Let LHS: (a + b + c)2 / (a2 + b2 + c2)
(a + b + c)2 / (a2 + b2 + c2) = (a + b + c)2/(a2 – b2 + c2 + 2b2)
= (a + b + c)2 / (a2 – b2 + c2 + 2ac) -(∵ b2 = ac)
= (a + b + c)2 / (a + b + c)(a – b + c) -(∵ (a + b + c)(a – b + c) = a2 – b2 + c2 + 2ac)
= (a + b + c) / (a – b + c)
= RHS
LHS = RHS
Hence, proved.
(iv) Given: a, b, c are in GP.
Using the property of geometric mean,
b2 = ac
Let LHS: 1/(a2 – b2) + 1/b2
On taking LCM, we get
1/(a2 – b2) + 1/b2 = (b2 + a2 – b2)/(a2 – b2)b2
= a2 / (a2b2 – b4)
= a2 / (a2b2 – (b2)2)
= a2 / (a2b2 – (ac)2) -(∵ b2 = ac)
= a2 / (a2b2 – a2c2)
= a2 / a2(b2 – c2)
= 1/ (b2 – c2)
= RHS
LHS = RHS
Hence, proved.
(v) Given: a, b, c are in GP.
Using the property of geometric mean,
b2 = ac
Let LHS: (a + 2b + 2c) (a – 2b + 2c)
Now, on expanding, we get
(a + 2b + 2c) (a – 2b + 2c) = a2 – 2ab + 2ac + 2ab – 4b2 + 4bc + 2ac – 4bc + 4c2
= a2 + 4ac – 4b2 + 4c2
= a2 + 4ac – 4(ac) + 4c2 -(∵ b2 = ac)
= a2 + 4c2
= RHS
LHS = RHS
Hence, proved.
Question 9. If a, b, c, d are in G.P., prove that:
(i) (ab – cd) / (b2 – c2) = (a + c) / b
(ii) (a + b + c + d)2 = (a + b)2 + 2(b + c)2 + (c + d)2
(iii) (b + c) (b + d) = (c + a) (c + d)
Solution:
(i) Given: a, b, c are in GP.
Using the property of geometric mean,
b2 = ac
bc = ad
c2 = bd
Let LHS: (ab – cd) / (b2 – c2)
(ab – cd) / (b2 – c2) = (ab – cd) / (ac – bd)
= (ab – cd)b / (ac – bd)b
= (ab2 – bcd) / (ac – bd)b
= [a(ac) – c(c2)] / (ac – bd)b
= (a2c – c3) / (ac – bd)b
= [c(a2 – c2)] / (ac – bd)b
= [(a + c) (ac – c2)] / (ac – bd)b
= [(a + c) (ac – bd)] / (ac – bd)b
= (a + c) / b
= RHS
LHS = RHS
Hence, proved.
(ii) Given: a, b, c are in GP.
Using the property of geometric mean,
b2 = ac
bc = ad
c2 = bd
Let RHS: (a + b)2 + 2(b + c)2 + (c + d)2
Now, on expanding, we get
(a + b)2 + 2(b + c)2 + (c + d)2 = (a + b)2 + 2 (a + b) (c + d) + (c + d)2
= a2 + b2 + 2ab + 2(c2 + b2 + 2cb) + c2 + d2 + 2cd
= a2 + b2 + c2 + d2 + 2ab + 2(c2 + b2 + 2cb) + 2cd
= a2 + b2 + c2 + d2 + 2(ab + bd + ac + cb +cd) -(∵ c2 = bd, b2 = ac)
(a + b + c)2 + d2 + 2d(a + b + c) = {(a + b + c) + d}2
RHS = LHS
Hence, proved.
(iii) Given: a, b, c are in GP.
Using the property of geometric mean,
b2 = ac
bc = ad
c2 = bd
Let LHS: (b + c) (b + d)
Now, on expanding, we get
(b + c) (b + d) = b2 + bd + cb + cd
= ac + c2 + ad + cd
= c (a + c) + d (a + c)
= (a + c) (c + d)
= RHS
LHS = RHS
Hence, proved.
Question 10. If a, b, c are in G.P., prove that the following are also in G.P.:
(i) a2, b2, c2
(ii) a3, b3, c3
(iii) a2 + b2, ab + bc, b2 + c2
Solution:
(i) Given: a, b, c are in GP.
Using the property of geometric mean,
b2 = ac
On squaring both the sides we get,
(b2)2 = (ac)2
(b2)2 = a2c2
Hence, proved a2, b2, c2 are in G.P.
(ii) Given: a, b, c are in GP.
By using the property of geometric mean,
b2 = ac
On squaring both the sides, we get
(b2)3 = (ac)3
(b2)3 = a3c3
(b3)2 = a3c3
Hence, proved a3, b3, c3 are in G.P.
(iii) Given: a, b, c are in GP.
Using the property of geometric mean,
b2 = ac
a2 + b2, ab + bc, b2 + c2 or (ab + bc)2 = (a2 + b2) (b2 + c2)
Let LHS: (ab + bc)2
Now, on expanding, we get
(ab + bc)2 = a2b2 + 2ab2c + b2c2
= a2b2 + 2b2(b2) + b2c2 -(∵ ac = b2)
= a2b2 + 2b4 + b2c2
= a2b2 + b4 + a2c2 + b2c2 -(∵ b2 = ac)
= b2(b2 + a2) + c2(a2 + b2)
= (a2 + b2)(b2 + c2)
= RHS
LHS = RHS
Hence, a2 + b2, ab + bc, b2 + c2 are in GP.
Question 11. If a, b, c, d are in G.P. prove that;
(i) (a2 + b2), (b2 + c2), (c2 + d2) are in G.P.
(ii) (a2 – b2), (b2 – c2), (c2 – d2) are in G.P.
(iii) 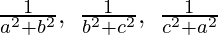 are in G.P.
are in G.P.
(iv) (a2 + b2 + c2), (ab + bc + cd), (b2 + c2 + d2) are in G.P.
Solution:
(i) Given: a, b, c, d are in G.P.
So, a, b = ar, c = ar2, d = ar3
Now,
(b2 + c2)2 = (a2 + b2)(c2 + d2)
(a2r2 + a2r4)2 = (a2 + a2r2)(a2r4 + a2r6)
a4(r2 + r4) = a2(1 + r2)a2r4(1 + r2)
a4r4(1 + r2)2 = a4r4(1 + r2)2
L.H.S = R.H.S
⇒ (b2 + c2)2 = (a2 + b2)(c2 + d2)
Hence, proved (a2 + b2), (b2 + c2), (c2 + d2) are in G.P.
(ii) Given: a, b, c, d are in G.P.
So, a, b = ar, c = ar2, d = ar3
Now,
(b2 – c2)2 = (a2 – b2)(c2 – d2)
(a2r2 – a2r4) = (a2 – a2r2)(a2r4 – a2r6)
a4(r2 – r4)2 = a2(1 – r2) a2r4 (1 – r2)
a4r4 (1 – r2)2 = a4r4 (1 – r2)2
L.H.S = R.H.S
⇒ (b2 – c2)2 = (a2 – b2)(c2 – d2)
Hence, proved (a2 – b2), (b2 – c2), (c2 – d2) are in G.P.
(iii) Given: a, b, c, d are in G.P.
So, a, b = ar, c = ar2, d = ar3
Now,
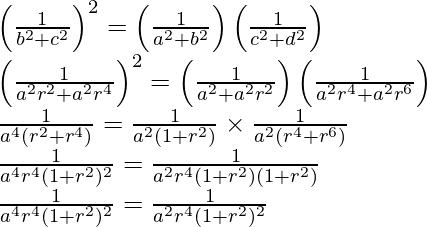
L.H.S = R.H.S
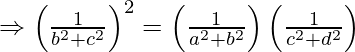
Hence, proved 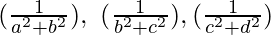 are in G.P.
are in G.P.
(iv) Given: a, b, c, d are in G.P.
So, a, b = ar, c = ar2, d = ar3
Now,
(ab + bc + cd)2 = (a2 + b2 + c2)(b2 + c2 + d2)
(a2r + a2r3 + a2r5)2 = (a2 + a2r2 + a2r4)(a2r2 + a2r4 + a2r6)
a4(r + r3 + r5)2 = a2(1 + r2 + r4) a2r2 ( 1 + r2 + r4)
a4r2(1 + r2 + r4)2 = a4r2(1 + r2 + r4)2
L.H.S = R.H.S
⇒ (ab + bc + cd)2 = (a2 + b2 + c2)(b2 + c2 + d2)
Hence, proved (a2 + b2 + c2), (ab + bc + cd), (b2 + c2 + d2) are in G.P.
Share your thoughts in the comments
Please Login to comment...