Question 1. From a group of 15 cricket players, a team of 11 players is to be chosen. In how many ways can this be done?
Solution:
We are given,
Total number of players = 15
Number of players to be chosen = 11
So, number of ways = 15C11
=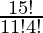
=
= 15 × 7 × 13
= 1365
Therefore, the total number of ways of choosing 11 players out of 15 is 1365.
Question 2. How many different boat parties of 8, consisting of 5 boys and 3 girls, can be made from 25 boys and 10 girls?
Solution:
We are given,
Total number of boys = 25
Total number of girls = 10
Boat party of 8 is to be made from 25 boys and 10 girls, by selecting 5 boys and 3 girls.
So, number of ways = 25C5 × 10C3
=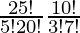
= 53130 × 120
= 6375600
Therefore, the total number of different boat parties that can be made is 6375600.
Question 3. In how many ways can a student choose 5 courses out of 9 courses if 2 courses are compulsory for every student?
Solution:
We are given,
Total number of courses = 9
Number of courses a students can have = 5
Out of 9 courses, 2 courses are compulsory. So, a student can choose from 3 (i.e., 5−2) courses only.
So, number of ways = 7C3
=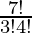
=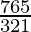
= 7 × 5
= 35
Therefore, the total number of ways in which a student can choose the subjects is 35.
Question 4. In how many ways can a football team of 11 players be selected from 16 players? How many of these will
(i) include 2 particular players?
(ii) exclude 2 particular players?
Solution:
Total number of players = 16
Number of players to be selected = 11
So, number of ways = 16C11
=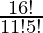
=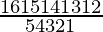
= 4×7×13×12
= 4368
(i) include 2 particular players?
As two particular players have to be kept in the team every time, we have to choose 9 players (11−2) out of the
14 players (16−2).
So, number of ways = 14C9
=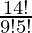
=
= 7×13×11×2
= 2002
(ii) exclude 2 particular players?
As 2 particular players are already removed, we have to select 11 players out of the remaining 14 players (16−2).
So, number of ways = 14C9
=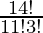
=
= 14×13×2
= 364
Therefore, the required number of ways are 4368, 2002, 364 respectively.
Question 5. There are 10 professors and 20 students out of whom a committee of 2 professors and 3 students is to be formed. Find the number of ways in which this can be done. Further, find in how many of these committees:
(i) a particular professor is included.
(ii) a particular student is included.
(iii) a particular student is excluded.
Solution:
We are given,
Total number of professor = 10
Total number of students = 20
It is given that a committee has to be formed by choosing 2 professors from 10 and 3 students from 20.
So, number of ways = 10C2 × 20C3
=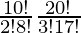
=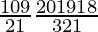
= 5×9×10×19×6
= 51300 ways
(i) a particular professor is included.
As one particular professor has to be selected in the committee every time, we have to choose 1 professor (2−1) out of the 9 professors (10−1). Number of ways for choosing students remain the same.
So, number of ways = 9C1 × 20C3
=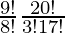
=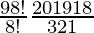
= 9×10×19×6
= 10260 ways
(ii) a particular student is included.
As one particular student has to be selected in the committee every time, we have to choose 2 professors (3−1) out of the 19 professors (20−1). Number of ways for choosing professors remain the same.
So, number of ways = 10C2 × 19C2
=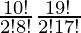
=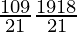
= 5×9×19×9
= 7695 ways
(iii) a particular student is excluded.
As one particular student has been removed from selection panel, we have to choose 3 students out of 19 students (20−1). Number of ways for choosing professors remain the same.
So, number of ways = 10C2 × 19C3
=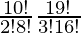
=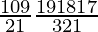
= 5×9×19×3×17
= 43605 ways
Therefore, the required number of ways are 51300, 10260, 7695, 43605 respectively.
Question 6. How many different products can be obtained by multiplying two or more of the numbers 3, 5, 7, 11 (without repetition)?
Solution:
Total number of ways will be sum of number of ways of multiplying two numbers, three numbers and four numbers.
So, number of ways = 4C2 + 4C3 + 4C4
=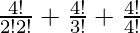
=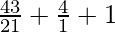
= 6 + 4 + 1
= 11
Therefore, the total number of ways of product is 11 ways.
Question 7. From a class of 12 boys and 10 girls, 10 students are to be chosen for the competition, at least including 4 boys and 4 girls. The 2 girls who won the prizes last year should be included. In how many ways can the selection be made?
Solution:
We are given,
Total number of boys = 12
Total number of girls = 10
Total number of girls for the competition = 10 + 2 = 12
As two particular girls have to be included, total students that can be selected = 10−2 = 8
So, number of ways = (12C6 × 8C2) + (12C5 × 8C3) + (12C4 × 8C4)
=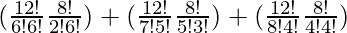
=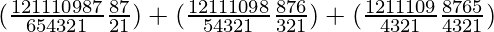
= (924 × 28) + (792 × 56) + (495 × 70)
= 25872 + 44352 + 34650
= 104874
Therefore, the total number of ways in which the selection can be made is 104874.
Question 8. How many different selections of 4 books can be made from 10 different books, if
(i) there is no restriction
(ii) two particular books are always selected
(iii) two particular books are never selected
Solution:
Total number of books = 10
Number of books to be selected = 4
(i) there is no restriction
Number of ways = Choosing 4 books out of 10 books = 10C4
=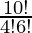
=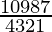
= 10×3×7
= 210
Therefore, the number of ways of selecting books if there is no restriction is 210.
(ii) two particular books are always selected
As we have to select two particular books every time, we can select 2 books (4−2) out of the remaining 8 books (10−2).
So, number of ways = 8C2
=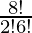
=
= 4×7
= 28
Therefore, the number of ways of selecting books if two particular books are always selected is 28.
(iii) two particular books are never selected
As two particular books have been removed, we have to choose 4 books out of the remaining 8 books (10−2).
So, number of ways = 8C4
=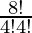
=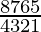
= 7×2×5
= 70
Therefore, the number of ways of selecting books if two particular books are never selected is 70.
Question 9. From 4 officers and 8 jawans in how many ways can 6 be chosen
(i) to include exactly one officer
(ii) to include at least one officer?
Solution:
Total number of officers = 4
Total number of jawans = 8
Total number of selections to be made = 6
(i) to include exactly one officer
Out of 6 selections, only 1 has to be an officer. So remaining 5 have to be jawans.
So, number of ways = (4C1) × (8C5)
=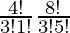
=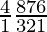
= 4×4×7×2
= 224
Therefore, the number of ways of selection if only one officer has to be included is 224.
(ii) to include at least one officer?
Out of 6 selections, at least 1 has to be an officer. So, we can choose from 1 to all 4 officers in our selections. And number of jawans would adjust according to that.
So, number of ways = (4C1 × 8C5) + (4C2 × 8C4) + (4C3 × 8C3) + (4C4 × 8C2)
=
=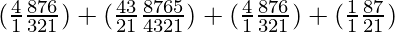
= (4 × 56) + (6 × 70) + (4 × 56) + (1 × 28)
= 224 + 420 + 224 + 28
= 896
Therefore, the number of ways of selection if at least one officer has to be included is 896.
Question 10. A sports team of 11 students is to be constituted, choosing at least 5 from class XI and at least 5 from class XII. If there are 20 students in each of these classes, in how many ways can the teams be constituted?
Solution:
Total number of students in XI = 20
Total number of students in XII = 20
Number of students to be selected in a team = 11
Now, at least 5 from class XI and 5 from class XII have to be selected.
So, number of ways = (20C6 × 20C5) + (20C5 × 20C6)
= 2 (20C6 × 20C5)
= 2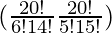
=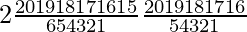
= 2×38760×15504
= 1201870080
Therefore, the number of ways in which the teams can be constituted is 1201870080.
Question 11. A student has to answer 10 questions, choosing at least 4 from each of part A and part B. If there are 6 questions in part A and 7 in part B, in how many ways can the student choose 10 questions?
Solution:
Total number of questions = 10
Questions in part A = 6
Questions in part B = 7
Number of questions a student can choose = 10
Now a student can choose at least 4 from each of part A and part B and total number of questions that he can choose must not exceed.
So, number of ways = (6C4 × 7C6) + (6C5 × 7C5) + (6C6 × 7C4)
=
=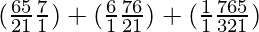
= (15×7) + (6×21) + (1×35)
= 105 + 126 + 35
= 266
Therefore, the number of ways of answering 10 questions is 266.
Share your thoughts in the comments
Please Login to comment...