Binomial Theorem is a theorem that is used to find the expansion of algebraic identity (ax + by)n. We can easily find the expansion of (x + y)2, (x + y)3, and others but finding the expansion of (x + y)21 is a tedious task and this task can easily be achieved using the Binomial Theorem or Binomial Expansion.
As the Binomial theorem is used to find the expansion of two terms it is called the Binomial Theorem. The exponent value in the Binomial expansion can also be a negative value or fraction value.
Let’s learn about the Binomial theorem, its expansion, formula, and others in detail in this article.
What is the Binomial Theorem?
The binomial theorem is used to solve binomial expressions simply. This theorem was first used somewhere around 400 BC by Euclid, a famous Greek mathematician.
It gives an expression to calculate the expansion of algebraic expression (a+b)n. The terms in the expansion of the following expression are exponent terms and the constant term associated with each term is called the coefficient of terms.
Binomial Theorem Statement
The Binomial theorem for the expansion of (a+b)n is stated as,
(a + b)n = nC0 anb0 + nC1 an-1 b1 + nC2 an-2 b2 + …. + nCr an-r br + …. + nCn a0bn
where n>0 and the nCk is the binomial coefficient.
Example: Find the expansion of (x + 5)6 using the binomial theorem.
Solution:
We know that here,
(a + b)n = nC0 anb0 + nC1 an-1 b1 + nC2 an-2 b2 + …. + nCr an-r br + …. + nCn a0bn
Thus, (x + 5)6 = 6C0 x650 + 6C1 x6-151 + 6C2 x6-252 + 6C3 x6-353 + 6C4 x6-454 + 6C5 x6-555 + 6C6 x6-656
= 6C0 x6 + 6C1 x55 + 6C2 x452 + 6C3 x353 + 6C4 x254 + 6C5 x155 + 6C6 x056
= x6 + 30x5 + 375x4 + 2500x3 + 9375x2 + 18750x + 15625
Binomial Expansion
Binomial Theorem is used to expand the algebraic identity (x + y)n. Hence it is also called the binomial expansion. The binomial expansion of (x + y)n with the help of the binomial theorem is,
(x+y)n = nC0 xny0 + nC1 xn-1y1 + nC2 xn-2 y2 + … + nCn-1 x1yn-1 + nCnx0yn
Using this expansion we get each term in the expansion of (x+y)nl
Example: Find the value of (x+y)2 and (x+y)3 using Binomial expansion.
Solution:
(x+y)2 = 2C0 x2y0 + 2C1 x2-1y1 + 2C2 x2-2 y2
⇒ (x+y)2 = x2 + 2xy + y2
And (x+y)3 = 3C0 x3y0 + 3C1 x3-1y1 + 3C2 x3-2 y2 + 3C3 x3-3 y3
⇒ (x+y)3 = x3 + 3x2y + 3xy2 + y3
⇒ (x+y)3 = x3 + 3xy(x+y) + y3
The binomial theorem formula gives the expansion of the algebraic identities in the form of a series. This formula is used to find the expansion up to n terms of the (a+b)n. The binomial expansion of (a+b)n can easily be represented with the summation formula.
The Binomial Theorem Formula for the expansion of (a+b)n is,
(a+b)n= ∑nr nCr an-r br
Where,
- n is a positive integer,
- a, b are real numbers, and 0 < r ≤ n
We can easily find the expansion of the various identities such as (x+y)7, (x+9)11, and others using the Binomial Theorem Formula. We can also find the expansion of (ax + by)n using the Binomial Theorem Formula,
The expansion formula for (ax + by)n is,
(ax + by)n = ∑nr nCr (ax)n-r (by)r
Where 0< r ≤ n.
Also using the combination formula we know that,
nCr = n! / [r! (n – r)!]
Binomial Theorem Expansion Proof
We can easily proof Binomial Theorem Expansion using the concept of Principle of Mathematical Induction
Let’s take x, a, n ∈ N, and then the Binomial Theorem says that,
(x+y)n = nC0 xny0 + nC1 xn-1y1 + nC2 xn-2 y2 + … + nCn-1 x1yn-1 + nCn x0yn
Proof:
For n = 1, we get
(x +y)1 = x +y which is true.
For n = 2,
(x +y)2 = (x + y) (x +y)
⇒ (x +y)2 = x2 + xy + xy + y2 (using distributive property of multiplication over addition)
⇒ (x +y)2 = x2 + 2xy + y2
which is also true.
Thus the theorem is true for n = 1 and n = 2.
Let’s take a positive integer k.
(x+y)k = kC0 xky0 + kC1 xk-1y1 + kC2 xk-2 y2 + … + kCk-1 x1yk-1 + kCk x0yk
Now consider the expansion for n = k + 1
(x + y) k+1 = (x + y) (x + y)k
⇒ (x + y) k+1 = (x + y) (xk + kC1 xk-1y1 + kC2 xk-2 y2 + … + kCr xk-ryr +….+ yk)
⇒ (x + y) k+1 = xk+1 + (1 + kC1)xky + (kC1 + kC2) xk-1y2 + … + (kCr-1 + kCr) xk-r+1yr + … + (kCk-1 + 1) xyk + yk+1
⇒ (x + y) k+1 = xk+1 + k+1C1xky + k+1C2 xk-1y2 + … + k+1Cr xk-r+1yr + … + k+1Ck xyk + yk+1
[As we know, nCr + nCr-1 = n+1Cr]
This result is true for n = k+1.
Thus, by the concept of mathematical induction, the result is true for all positive integers ‘n’. Proved.
Properties of Binomial Theorem
There are various properties related to the binomial theorem, some of those properties are as follows:
- Number of Terms: In the binomial Expansion of (x + y)n using the binomial theorem, there are n+1 terms and coefficients.
- The first and last terms in the binomial expansion of (x + y)n are xn and yn, respectively.
- General Term: In the binomial expansion of (x + y)n the general term can be represented as T(r + 1) and is given by T(r + 1) = nCr × x(n-r) × yr.
- Pascal’s Triangle: The binomial coefficients in the expansion are arranged in Pascal’s triangle which is the pattern of number where each number is the sum of the two numbers above it.
- Specific Values: When n is a non-negative integer, the expansion simplifies for specific values of n:
- (a + b)0 = 1
- (a + b)1 = a + b
- (a + b)2 = a2 + 2ab + b2
- (a + b)3 = a3 + 3a2b + 3ab2 + b3
- and so on…
- Binomial Coefficients Symmetry: In the binomial expansion of (x + y)n, the rth term from the end is the (n – r + 2)th term from the beginning.
- If n is even, then in the expansion of (x + y)n, the middle term is ((n/2) + 1). If n is odd, then the middle terms are ((n + 1)/2) and ((n + 3)/2) in the expansion of (x + y)n.
Pascal’s Triangle Binomial Expansion
The number associated with the terms of the binomial expansion is called the coefficient of the binomial expansion. These variables can easily be found using Pascal’s Triangle or by using combination formulas.
Binomial Theorem Coefficients
After examining the coefficient of the various terms in the expansion of algebraic identities using the binomial theorem, we have observed a trend in the coefficient of the terms of the expansion. The trend is that the coefficient of the terms in the expansion of the binomial terms is directly similar to the rows of the Pascal triangle.
For example, the coefficient of each term in the expansion of the (x+y)4 is directly equivalent to the terms in the 4th row of the Pascal Triangle.
Now, let’s learn about Pascal Triangle in detail.
Pascal Triangle
Pascal Triangle is an alternative method of the calculation of coefficients that come in binomial expansions, using a diagram rather than algebraic methods.
In the diagram shown below, it is noticed that each number in the triangle is the sum of the two directly above it. This pattern continues indefinitely to obtain coefficients of any index of the binomial expression.
When we observe the pattern of the coefficients of the expansion (a + b)n, Pascal’s triangle for the pattern of the coefficients of the expansion (a + b)7 is shown in the figure below:
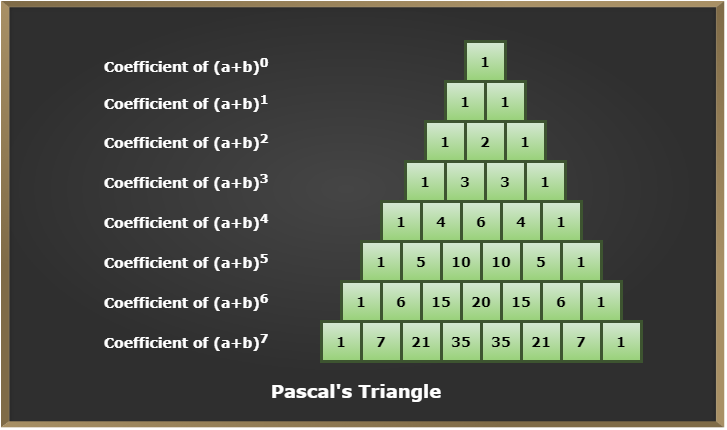
Learn More: Pascal’s Triangle
Thus, from the above diagram, the expansion of small powers of n (e.g. n=0, 1, 2, 3, 4, 5, 6, 7) can be calculated as:
- (a + b)0 = 1
- (a + b)1 = a + b
- (a + b)2 = a2 + 2ab +b2
- (a + b)3 = a3 + 3a2b + 3ab2 + b3
- (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
- (a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
- (a + b)6 = a6 + 6a5b + 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + b6
- (a + b)7 = a7 + 7a6b + 21a5b2 + 35a4b3 + 35a3b4 + 21a2b5 + 7ab6 + b7
In this way, the expansion from (a + b)0 to (a + b)7 is obtained by the application of Pascal’s Triangle. But finding (a + b)15 is really a long process using Pascal’s triangle. So, here we use combinations formulas.
Combinations
The combination formulas are also widely used to find coefficients of the various terms in the expansion of the binomial theorem.
The combination formula used for choosing r objects out of n total objects is widely used in the binomial expansion and it is defined as,
nCr = n! / [r! (n – r)!]
Also, some common combination formulas used in the Binomial Expansion are,
- nCn = nC0 = 1
- nC1 = nCn-1 = n
- nCr = nCr-1
Some properties of combination which are widely used in simplifying binomial expansion are,
- C1 + C2 + C3 + C4 + …….Cn = 2n
- C0 + C2 + C4 + …. = C1 + C3 + C5 + ……. = 2n-1
- C0 – C1 + C2 – C3 + C4 – C5 + …. = 0
- C1 + 2C2 + 3C3 + 4C4 + …….nCn = n2n-1
- C1 – 2C2 + 3C3 – 4C4 + …….(-1)nnCn = 0
- C12 + C22 + C32 + C42 + …….Cn2 = (2n)! / (n!)2
Learn more about, Permutations and Combinations
Binomial Expansion for Negative Exponent
The binomial theorem is also used for finding the expansion of the identities which have negative exponents. The coefficients terms in the negative expansion are similar in magnitude to the terms in the corresponding positive exponent.
Some of the simplified expansions of the negative exponents which are widely used are,
- (1 + x)-1 = 1 – x + x2 – x3 + x4 – x5 + …….
- (1 – x)-1 = 1 + x + x2 + x3 + x4 + x5 + …….
- (1 + x)-2 = 1 – 2x + 3x2 – 4x3 + ……..
- (1 – x)-2 = 1 + 2x + 3x2 + 4x3 + ……..
These expansions are easily proved using binomial expansion and replacing (+) with (-)
Important Terms of Binomial Theorem
Various terms related to Binomial Expansion that is used widely include,
General Term of Expansion
The general term of the binomial expansion signifies a term that produces all the terms of the binomial expansion by simply replacing the value of one component of the term.
For example in the binomial expansion of (x+y)n the general term is,
Tr+1 = nCr xn-ryr
Where, 0 ≤ r ≤n
Substituting the values of r in the above term we get all the terms of the expansion. We observe that r takes n+1 values which is also true as there are n+1 terms in the expansion of (x+y)n
Middle Term of Expansion
We know that the total number of terms in the expansion of (x + y)n is n + 1. And so the middle term in the binomial expansion of the (x+y)n depends on the value of n. The value of n can be either even or odd which decides the number/numbers and values of the middle term.
- If n is even then we have odd (n+1) terms in the expansion of (x+y)n. Thus, there is one middle term, in this case, and the middle term is (n/2 + 1)th term.
- If n is odd then we have even (n+1) terms in the expansion of (x+y)n. Thus, there are two middle terms, in this case, and the middle terms are the (n/2)th term and (n/2 + 1)th term.
Learn more about, General and Middle Terms
Identifying a Particular Term in Expansion
Any particular term can easily be identified in the expansion of (x+y)n. We follow two steps to get a particular term in the expansion of (x+y)n.
For example, if we have to find the term pth term in the expansion of (x+y)n.
Step 1: Find the general term in the expansion of (x+y)n. The general term is,
Tr+1 = nCr xn-ryr
Step 2: Then substitute the value of ‘r’ for the value of the term which we have to find. In this case, r = p and then simplify to get the pth term.
Example: Find the 6th term in the expansion of (3x + 4)8
Solution:
The general term in the expansion of (3x + 4)8 is,
Tr+1 = 8Cr(3x)8-r(4)r
For 6th term r = 5
T6 = T5+1 = 8C5(3x)8-5(4)5
Simplifying the above term we get our answer,
T6 = 8C5(3x)8-5(4)5
= (8.7.6/3.2.1)(27)(1024)x3
= 1593648x3
Term Independent of X in Expansion
The term independent of ‘x’ can easily be identified in the expansion of (x+y)n. We follow two steps to get a particular term in the expansion of (x+y)n.
For example, if we have to find the term independent of ‘x’ term in the expansion of (x+y)n.
Step 1: Find the general term in the expansion of (x+y)n. the general term is,
Tr+1 = nCr xn-ryr
Step 2: Then substitute the value of ‘r’ as r = n to get rid of the x term.
Example: Find the term independent of x in the expansion of (2x + 1)8
Solution:
The general term in the expansion of (2x + 1)8 is,
Tr+1 = 8Cr(2x)8-r(1)r
For the term independent of x
8-r = 0
r = 8
T9 = T8+1 = 8C8(2x)8-8(1)8
Simplifying the above term we get our answer,
T9 = 8C8(2x)8-8(1)8
= (1)(1)(1)
= 1
Numerically Greatest Term of Expansion
We can easily find the numerically greatest term in the expansion of (1+x)n. The formula to find the greatest term in the expansion of (1+x)n is,
[(n+1)|x|]/(1+|x|)
While using this formula we have to make sure that the expansion is in (1+x)n form only, and |x| gives only the numerical value.
Applications of Binomial Theorem
The Binomial Theorem has various applications it is used for a variety of the purposes such as,
- Finding Remainder in the division of very large numbers.
- Finding Last Digits of a Number
- Checking the Divisibility
Finding Remainder using Binomial Theorem
This can easily be understood with the help of the following example.
Example: Find the remainder when 297 is divided by 15
Solution:
(297 / 15) = [2(24)24 / 15)]
= [2(15 + 1)24 / 15]
As each term of the expansion of (1 + 15)24 contains 15 except the first term which is only 1.
Thus, Remainder when 297 is divided by 15 is 1.
Finding the Last Digits of a Number
How to find the last digit of an expansion can be understood using the example,
Example: Find the last digit of (7)10
Solution:
(7)10 = (49)5 = (50-1)5
(50-1)5 = 5C0 (50)5 − 5C1 (50)4 + 5C2 (50)3 − 5C3 (50)2 + 5C4 (50) − 5C5
= 5C0 (50)5 − 5C1 (50)4 + 5C2 (50)3 − 5C3 (50)2 + 5(50) − 1
= 5C0 (50)5 − 5C1 (50)4 + 5C2 (50)3 − 5C3 (50)2 + 249
A multiple of 50 + 249 = 50K + 249
Thus, the last digit is 9.
Binomial Theorem for Any Index
The Binomial Theorem for any index, including non-integer and negative indices, generalizes the familiar binomial expansion that applies to positive integer exponents. This generalized form involves the use of binomial coefficients that are defined for any real number index using the concept of factorial functions extended to the gamma function for non-integer values.
Multinomial Theorem
We know that the binomial theorem expansion of (x + a)n is,
(x+a)n = n∑r nCr xn – r ar
Where n∈N
We can generalize this result to get the expansion of,
(x1 + x2 + … +xk)n = ∑(r1 + r2 + …. + rk = n) [n! / r1!r2!…rk!] x1r1 x2r2 …xkrk
The general term in the above expansion is
[n! / r1!r2!…rk!] x1r1 x2r2 …xkrk
The number of terms in the above expansion is equal to the number of non-negative integral solutions of the equation r1 + r2 + … + rk = n
Each solution of this equation gives a term in the above multinomial expansion. The total number of solutions can be given by n + k – 1Ck −1.
People Also Read:
Binomial Distribution and Binomial Coefficients
Binomial Distribution
The binomial distribution models the number of successes in a fixed number of independent and identical Bernoulli trials (experiments with two possible outcomes: success or failure). It’s characterized by two parameters: nn (the number of trials) and pp (the probability of success in each trial).
Hypergeometric Distribution
The hypergeometric distribution models the probability of obtaining a specific number of successes in a sample of a fixed size drawn without replacement from a finite population containing a known number of successes and failures.
Also Check:
Examples on Binomial Theorem
Example 1: Expand the binomial expression (2x + 3y)2.
Solution:
(2x + 3y)2 = (2x)2 + 2(2x)(3y) + (3y)2
= 4x2 + 12xy + 9y2
Example 2: Expand the following (1 – x + x2)4
Solution:
Put 1 – x = y
Then,
(1 – x + x2)4 = (y + x2)4
= 4C0y4(x2)0 + 4C1y3(x2)1 + 4C2y2(x2)2 +4C3y(x2)3 +4C4(x2)4
= y4 + 4y3x2 + 6y2x4 + 4yx6 + x8
= (1 – x)4 + 4(1 – x)3x2 + 6(1 – x)2x4 + 4(1 – x)x6 + x8
= 1 – 4x + 10x2 – 16x3 + 19x4 – 16x5 + 10x6– 4x7 + x8
Example 3: Find the 4th term from the end in the expansion of ((x3/2) – (2/x2))8.
Solution:
Since rth term from the end in the expansion of (a + b)n is
(n – r + 2)th term from the beginning.
Therefore, 4th term from the end is 8 – 4 + 2,
i.e., 6th term from the beginning, which is given by
T6 = 8C5(x3/2)3(-2/x2)5
= 8C3(x9/8)(-32/x10)
= -224/x
Example 4: Find the middle term (terms) in the expansion of ((p/x) + (x/p))9
Solution:
Since the power of binomial is odd. Therefore, we have two middle terms
which are 5th and 6th terms. These are given by
T5 = 9C4(p/x)5(x/p)4
= 9C4(p/x)
= 126(p/x)
T6 = 9C5(p/x)4(x/p)5
= 9C5(x/p)
= 126(x/p)
Example 5: Find the 3th term in the expansion of (2x + 1)4
Solution:
The general term in the expansion of (2x + 1)4 is,
Tr+1 = 4Cr(2x)4-r(1)r
For 3th term r = 2
T3 = T2+1 = 4C2(2x)4-2(1)2
Simplifying the above term we get our answer,
T3 = 4C2(2x)4-2(1)2
= (6)(4)x2
= 24x2
Example 6: Find the term independent of x in the expansion of (3x + 2)8
Solution:
The general term in the expansion of (2x + 1)8 is,
Tr+1 = 8Cr(3x)8-r(2)r
For the term independent of x
8-r = 0
r = 8
T9 = T8+1 = 8C8(3x)8-8(2)8
Simplifying the above term we get our answer,
T9 = 8C8(3x)8-8(2)8
= (1)(1)(256)
= 256
Example 7: Find the binomial expansion of (x3 + 1)3.
Solution:
We know that,
(x + y)n = nC0 xny0 + nC1 xn-1y1 + nC2 xn-2 y2 + … + nCn-1 x1yn-1 + nCn x0yn
(x3 + 1)3 = 3C0 (x3)310 + 3C1 (x3)211 + 3C2 (x3)112+ 3C3 (x3)013
(x3 + 1)3 = (1)x9 + (3)x6 + (3)x3 + (1)
(x3 + 1)3 = x9 + 3x6 + 3x3 + 1
FAQs on Binomial Theorem
What Is the Binomial Theorem?
The binomial theorem is the basic theorem which provides an expansion to algebraic identity such as (x+y)n
(x+y)n = nC0 xny0 + nC1 xn-1y1 + nC2 xn-2 y2 + … + nCn-1 x1yn-1 + nCn x0yn
What Is the General Term in Binomial Theorem?
The general term is the binomial theorem expansion of (x+y)n is,
Tr+1 = nCr xn-ryr
where, 0≤r≤n
Substituting the values of r in the above term we get all the terms of the expansion.
What Is the Constant Term in the Binomial Theorem?
The term in the binomial theorem expansion which is free from the variables is called the constant term.
What is the Binomial Theorem formula?
The Binomial theorem is used to find the expansion of the algebraic terms of the form(x + y)n. The formula of the binomial expansion is
(x + y)n = Σrn nCr xn – r · yr
What are the number of terms in the expansion of (x + a)n + (x-a)n?
The number of terms in the expansion of (x + a)n + (x-a)n is given with the help of the formula,
- If n is even (n+2)/2
- If n is odd (n+1)/2
Share your thoughts in the comments
Please Login to comment...