Class 11 RD Sharma Solutions – Chapter 30 Derivatives – Exercise 30.4 | Set 3
Last Updated :
16 May, 2021
Question 21. Differentiate (2x2 – 3) sin x with respect to x.
Solution:
We have,
=> y = (2x2 – 3) sin x
On differentiating both sides, we get,
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{d}{dx}[(2x^2 - 3) sin x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-23478925adad7c569a16ec1407996399_l3.png)
On using product rule we get,
= 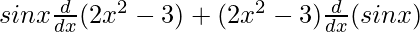
= 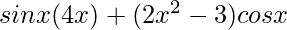
= 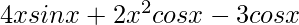
Question 22. Differentiate 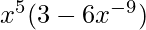 with respect to x.
with respect to x.
Solution:
We have,
=> y = 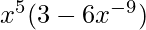
On differentiating both sides, we get,
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{d}{dx}[x^5(3-6x^{-9})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f739249b8d28cb39666bf9be34e272e2_l3.png)
On using product rule we get,
= 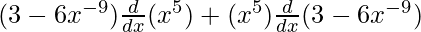
= ![Rendered by QuickLaTeX.com (3-6x^{-9})(5x^4)+(x^5)[-(6)(-9)x^{-10}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-76dcaf79b4659fabe6ec901bb5af24ae_l3.png)
= 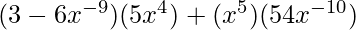
= 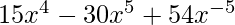
Question 23. Differentiate 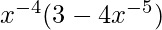 with respect to x.
with respect to x.
Solution:
We have,
=> y = 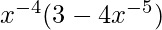
On differentiating both sides, we get,
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{d}{dx}[x^{-4}(3-4x^{-5})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9a178d6ac10ca90500c71f268f7ae176_l3.png)
On using product rule we get,
= 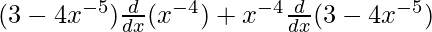
= ![Rendered by QuickLaTeX.com (3-4x^{-5})(-4x^{-5})+x^{-4}[-(4)(-5)x^{-6}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-04100b25c08f38971f8b43d29f3ab4d0_l3.png)
= ![Rendered by QuickLaTeX.com (3-4x^{-5})(-4x^{-5})+x^{-4}[20x^{-6}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6e3c4009129387845330dbd7fd3021e7_l3.png)
= 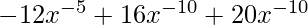
= 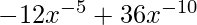
= 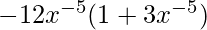
Question 24. Differentiate 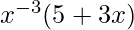 with respect to x.
with respect to x.
Solution:
We have,
=> y = 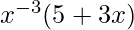
On differentiating both sides, we get,
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{d}{dx}[x^{-3}(5+3x)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-638b951bd41c96d511a09944372d450f_l3.png)
On using product rule we get,
= 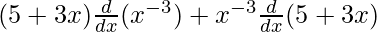
= 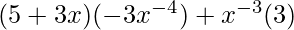
= 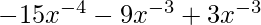
= 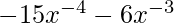
= 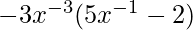
Question 25. Differentiate 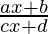 with respect to x.
with respect to x.
Solution:
We have,
=> y = 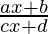
On differentiating both sides, we get,
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{d}{dx}[\frac{ax+b}{cx+d}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f62bb97d91c7a9e0ff3991df8b4f72a3_l3.png)
On using product rule we get,
= 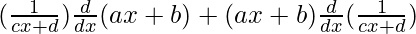
= ![Rendered by QuickLaTeX.com (\frac{1}{cx+d})(a)+(ax+b)\left[\frac{-1}{(cx+d)^{2}}×c\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-41b504c54711152b566a9b0a0b79da52_l3.png)
= ![Rendered by QuickLaTeX.com (\frac{a}{cx+d})+(ax+b)\left[\frac{-c}{(cx+d)^{2}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-67877afa88d2494c34d0ce62619490c5_l3.png)
= 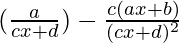
= 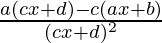
= 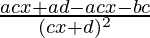
= 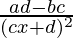
Question 26. Differentiate (ax + b)n (cx + d)m with respect to x.
Solution:
We have,
=> y = (ax + b)n (cx + d)m
On differentiating both sides, we get,
![Rendered by QuickLaTeX.com \frac{dy}{dx}=\frac{d}{dx}[(ax + b)^n (cx + d)^m]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1c6f5ddcc4af74ce36d5c175fae5da5d_l3.png)
On using product rule we get,
= ![Rendered by QuickLaTeX.com (cx + d)^m\frac{d}{dx}[(ax + b)^n]+(ax + b)^n\frac{d}{dx}[(cx + d)^m]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-93b9b91ffb413015450e599922f8e2a9_l3.png)
= ![Rendered by QuickLaTeX.com (cx + d)^m[na(ax + b)^{n-1}]+(ax + b)^n[mc(cx + d)^{m-1}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-45c69cf383be7fc3fd3294c940c49add_l3.png)
= 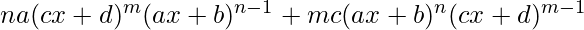
= ![Rendered by QuickLaTeX.com (cx + d)^{m-1}(ax + b)^{n-1}[na(cx+d)+mc(ax + b)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-37d466ed4d2571e70a56087933f91425_l3.png)
Question 27. Differentiate in two ways, using product rule and otherwise, the function (1 + 2 tan x) (5 + 4 cos x). Verify that the answer are the same.
Solution:
We have,
=> y = (1 + 2 tan x) (5 + 4 cos x)
On using product rule we get,
![Rendered by QuickLaTeX.com \frac{d}{dx}[(1 + 2 tan x) (5 + 4 cos x)]=(5 + 4 cos x)\frac{d}{dx}(1+2tanx)+(1+2tanx)\frac{d}{dx}(5+4cosx)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-74eb6aa17e6823e5526095cb7d976385_l3.png)
= 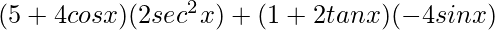
= 10 sec2 x + 8 cos x sec2 x − 4 sin x − 8 sin x tan x
= 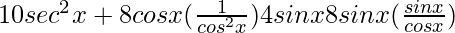
= 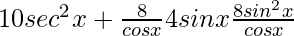
= 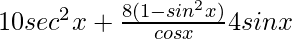
= 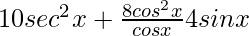
= 10 sec2 x + 8 cos x − 4 sin x
By using an alternate method, we have,
![Rendered by QuickLaTeX.com \frac{d}{dx}[(1 + 2 tan x) (5 + 4 cos x)]=\frac{d}{dx}(5+4cosx+10tanx+8tanxcosx)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-042c220db63ae144c108cc2ff6499828_l3.png)
= 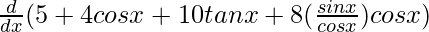
= 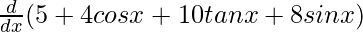
On using chain rule, we get,
= 0 − 4 sin x + 10 sec2 x + 8 cos x
= 10 sec2 x + 8 cos x − 4 sin x
Hence proved.
Question 28. Differentiate each of the following functions by the product rule and the other method and verify that answer from both the methods is the same.
(i) (3x2 + 2)2
Solution:
We have,
=> y = (3x2 + 2)2
On using product rule we get,
![Rendered by QuickLaTeX.com \frac{d}{dx}[(3x^2+2)^2]=(3x^2+2)\frac{d}{dx}(3x^2+2)+(3x^2+2)\frac{d}{dx}(3x^2+2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b98ae048db8487438aa64776d96a459f_l3.png)
= 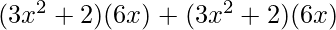
= 12x (3x2 + 2)
= 36 x3 + 24x
By using an alternate method, we have,
![Rendered by QuickLaTeX.com \frac{d}{dx}[(3x^2+2)^2]=\frac{d}{dx}[9x^4+4+12x^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-18b7145b80727bc2c83ba4b0de2d2fb8_l3.png)
On using chain rule, we get,
= 36 x3 + 0 + 24 x
= 36 x3 + 24x
Hence proved.
(ii) (x + 2)(x + 3)
Solution:
We have,
=> y = (x + 2)(x + 3)
On using product rule we get,
![Rendered by QuickLaTeX.com \frac{d}{dx}[(x + 2)(x + 3)]=(x+3)\frac{d}{dx}(x+2)+(x+2)\frac{d}{dx}(x+3)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8e66b3a5c9810c62a59ff3f3a9d20ce4_l3.png)
= (x+3)(1)+(x+2)(1)
= x + 3 + x + 2
= 2x + 5
By using an alternate method, we have,
![Rendered by QuickLaTeX.com \frac{d}{dx}[(x + 2)(x + 3)]=\frac{d}{dx}[x^2+5x+6]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7f5d864687137fa546c885553e8ae47f_l3.png)
On using chain rule, we get,
= 2x + 5
Hence proved.
(iii) (3 sec x − 4 cosec x) (−2 sin x + 5 cos x)
Solution:
We have,
=> y = (3 sec x − 4 cosec x) (−2 sin x + 5 cos x)
On using product rule we get,
![Rendered by QuickLaTeX.com \frac{d}{dx}[(3secx−4cosecx)(−2sinx+5cosx)]=(−2sinx+5cosx)\frac{d}{dx}(3secx−4cosecx)+(3secx−4cosecx)\frac{d}{dx}(−2sinx+5cosx)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b26fe43f2a1da3341ed84125ea3bfb85_l3.png)
= (−2 sin x + 5 cos x) (3 sec x tan x + 4 cot x cosec x)+ (3 sec x − 4 cosec x) (−2 cos x − 5 sin x)
= −6 sin x sec x tan x − 8 sin x cot x cosec x + 15 cos x sec x tan x + 20 cos x cot x cosec x − 6 sec x cos x − 15 sec x sin x + 8 cosec x cos x + 20 cosec x sin x
= −6 tan2 x − 8 cot x + 15 tan x + 20 cot2 x − 6 − 15 tan x + 8 cot x + 20
= − 6 − 6 tan2 x + 20 cot2 x + 20
= −6 (1 + tan2 x) + 20 (cot2 x + 1)
= −6 sec2 x + 20 cosec2 x
By using an alternate method, we have,
![Rendered by QuickLaTeX.com \frac{d}{dx}[(3secx−4cosecx)(−2sinx+5cosx)]=\frac{d}{dx}(−6secxsinx+15secxcosx+6cosecxsinx-20cosecxcosx)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d205a6270927e418930c6e51ef60a5b3_l3.png)
= 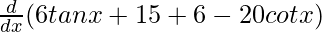
= 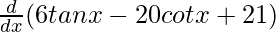
On using chain rule, we get,
= −6 sec2 x − (−20 cosec2 x)
= −6 sec2 x + 20 cosec2 x
Hence proved.
Share your thoughts in the comments
Please Login to comment...