Question 1. Find the distance between the following pairs of points:
(i) P(1, −1, 0) and Q (2, 1, 2)
Solution:
Given: The points P(1, −1, 0) and Q(2, 1, 2)
By using distance formula, the distance between any two points (a, b, c) and (d, e, f) is given as follows:

Hence, distance between P(1, −1, 0) and Q(2, 1, 2) is given by,
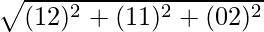
=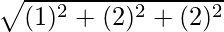
=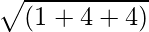
=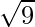
= 3
∴ The Distance between P and Q is 3 units.
(ii) A (3, 2, −1) and B (−1, −1, −1)
Solution:
Given: The points A (3, 2, −1) and B (−1, −1, −1)
By using distance formula, The distance between any two points (a, b, c) and (d, e, f) is given by:

Hence, distance between A (3, 2, −1) and B (−1, −1, −1) is given by,
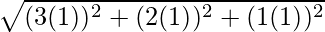
=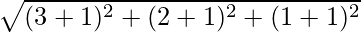
=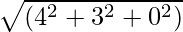
=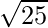
= 5
∴ The Distance between A and B is 5 units.
Question 2. Find the distance between the points P and Q having coordinates (−2, 3, 1) and (2, 1, 2).
Solution:
Given: The points P(− 2, 3, 1) and Q(2, 1, 2)
By using distance formula, the distance between any two points (a, b, c) and (d, e, f) is given by,

Hence, distance between P(−2, 3, 1) and Q(2, 1, 2) is given by,
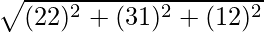
=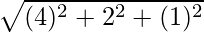
=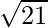
∴ The Distance between the given two points is 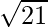 units.
units.
Question 3. Using distance formula prove that the following points are collinear:
(i) A(4, −3, −1), B(5, −7, 6) and C(3, 1, −8)
Solution:
Given: The points A(4, −3, −1), B(5, −7, 6) and C(3, 1, −8)
Points A, B and C are collinear if AB + BC = AC or AB + AC = BC or AC + BC = AB
By using the formula, the distance between any two points (a, b, c) and (d, e, f) is given by,

Hence, distance between A(4, −3, −1) and B(5, −7, 6) is given by,
AB =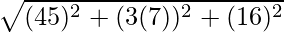
=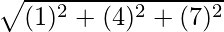
AB =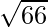
Now, Distance between B(5, −7, 6) and C(3, 1, −8) is given by,
BC =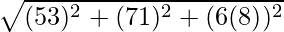
=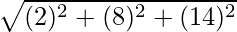
BC = 2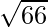
Also, Distance between A(4, −3, −1) and C(3, 1, −8) is given by,
AC =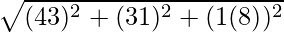
=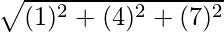
AC =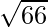
Clearly, AB + AC =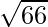 +
+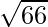 = 2
= 2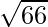 = BC
= BC
∴The points A, B and C are collinear.
(ii) P (0, 7, -7), Q (1, 4, -5) and R (-1, 10, -9)
Solution:
Given: The points P (0, 7, −7), Q (1, 4, −5) and R (−1, 10, −9)
Points P, Q and R are collinear if PQ + QR = PR or PQ + PR = QR or PR + QR = PQ
By using the formula, distance between any two points (a, b, c) and (d, e, f) is given by,

Hence, distance between P (0, 7, −7), Q (1, 4, −5) is given by,
PQ =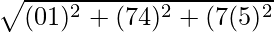
=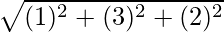
PQ =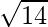
Now, Distance between Q (1, 4, −5) and R (−1, 10, −9) is given by,
QR =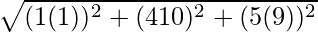
=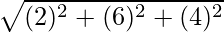
QR = 2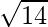
Also, Distance between P (0, 7, −7) and R (−1, 10, −9) is given by,
PR =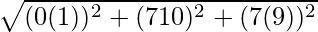
=
PR=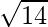
Clearly, PQ+ PR=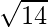 +
+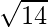 = 2
= 2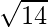 = QR
= QR
∴The points P, Q and R are collinear.
(iii) A(3, -5, 1), B(-1, 0, 8) and C(7, -10, -6)
Solution:
Given: The points A(3, -5, 1), B(-1, 0, 8) and C(7, -10, -6)
Points A, B and C are collinear if AB + BC = AC or AB + AC = BC or AC + BC = AB
By using the formula, the distance between any two points (a, b, c) and (d, e, f) is given by,

Hence, distance between A(3, -5, 1) and B (-1, 0, 8) is given by,
AB =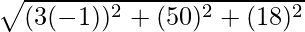
=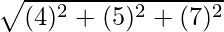
AB =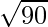
Now, Distance between B(-1, 0, 8) and C(7, -10, -6) is given by,
BC =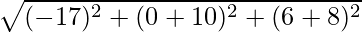
=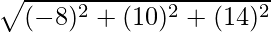
=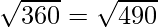
BC =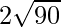
Also, Distance between A(3, -5, 1) and C(7, -10, -6) is given by,
AC =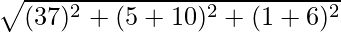
=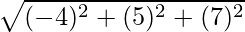
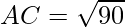
Clearly, AB + AC =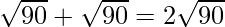 = BC
= BC
∴The points A, B and C are collinear.
Question 4. Determine the points in which are equidistant from points A(1, -1, 0), B(2, 1, 2), and C(3, 2, -1) in
(i) xy-plane
Solution:
Given: The points A(1, -1, 0), B(2, 1, 2) and C(3, 2, -1)
We know z = 0 in xy-plane. So let P(x, y, 0) be any point in xy-plane
We are given: PA = PB = PC
⇒ PA2 = PB2 = PC2
By using the formula, the distance between any two points (a, b, c) and (d, e, f) is given by,

We know PA2 = PB2
So, (x – 1)2+ (y + 1)2 = (x – 2)2 + (y – 1)2 + 4
⇒ x2+ 1 – 2x + y2 + 1 + 2y = x2+ 4 – 4x + y2 + 1 – 2y + 4
⇒ – 2x + 2 + 2y = 9 – 4x – 2y
⇒ – 2x + 2 + 2y – 9 + 4x + 2y = 0
⇒ 2x + 4y – 7 = 0
⇒ 2x = – 4y + 7 ……(a)
Since, PA2 = PC2
So, (x – 1)2+ (y + 1)2 = (x – 3)2 + (y – 2)2 + 1
⇒ x2+ 1 – 2x + y2 + 1 + 2y = x2+ 9 – 6x + y2 + 4 – 4y + 1
⇒ – 2x + 2 + 2y = 14 – 6x – 4y
⇒ – 2x + 2 + 2y – 14 + 6x + 4y = 0
⇒ 4x + 6y – 12 = 0
⇒ 2(2x + 3y – 6) = 0
Now substitute the value of 2x (obtained in equation (a)), we get
7 – 4y + 3y – 6 = 0
⇒ – y + 1 = 0 ⇒ y = 1
By substituting the value of y back in equation (a) we get,
2x = 7 – 4y
⇒ 2x = 7 – 4(1)
⇒ 2x = 3 ⇒ x = 3/2
∴The point P (3/2, 1, 0) in xy-plane is equidistant from A, B and C.
(ii) yz-plane
Solution:
We know x = 0 in yz-plane. Let Q(0, y, z) any point in yz-plane
According to the question: QA = QB = QC
⇒ QA2 = QB2 = QC2
By using the formula, the distance between any two points (a, b, c) and (d, e, f) is given by,

We know, QA2 = QB2
So, 1 + z2+ (y + 1)2 = (z – 2)2 + (y – 1)2 + 4
⇒ z2+ 1 + y2 + 1 + 2y = z2+ 4 – 4z + y2 + 1 – 2y + 4
⇒ 2 + 2y = 9 – 4z – 2y
⇒ 2 + 2y – 9 + 4z + 2y = 0
⇒ 4y + 4z – 7 = 0
⇒ 4z = –4y + 7
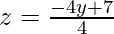 ……. (1)
……. (1)
Since, QA2 = QC2
So, 1 + z2+ (y + 1)2 = (z + 1)2 + (y – 2)2 + 9
⇒ 2+ 1 + y2 + 1 + 2y = z2+ 1 + 2z + y2 + 4 – 4y + 9
⇒ 2 + 2y = 14 + 2z – 4y
⇒ 2 + 2y – 14 – 2z + 4y = 0
⇒ –2z + 6y – 12 = 0
⇒ 2(–z + 3y – 6) = 0
Substituting the value of z [obtained from (1)] we get:
12y + 4y – 7 – 24 = 0
⇒ 16y – 31 = 0 ⇒ y = 31/16
Substituting the value of y back in equation (1), we get z = -3/16
∴The point Q (0, 31/16, -3/16) in yz-plane is equidistant from A, B and C.
(iii) zx-plane
Solution:
We know y = 0 in xz-plane. Let R(x, 0, z) any point in xz-plane
According to the question: RA = RB = RC
⇒ RA2 = RB2 = RC2
By using the formula, the distance between any two points (a, b, c) and (d, e, f) is given by,

We know, RA2 = RB2
So, 1 + z2+ (x – 1)2 = (z – 2)2 + (x – 2)2 + 1
⇒ z2+ 1 + x2 + 1 – 2x = z2+ 4 – 4z + x2 + 4 – 4x + 1
⇒ 2 – 2x = 9 – 4z – 4x
⇒ 2 + 4z – 9 + 4x – 2x = 0
⇒ 2x + 4z – 7 = 0
⇒ 2x = –4z + 7 …………(1)
Since, RA2 = RC2
So, 1 + z2+ (x – 1)2 = (z + 1)2 + (x – 3)2 + 4
⇒ z2+ 1 + x2 + 1 – 2x = z2+ 1 + 2z + x2 + 9 – 6x + 4
⇒ 2 – 2x = 14 + 2z – 6x
⇒ 2 – 2x – 14 – 2z + 6x = 0
⇒ –2z + 4x – 12 = 0
⇒ 2(2x) = 12 + 2z
Substituting the value of 2x [obtained from equation (1)] we get,
2(–4z + 7) = 12 + 2z
⇒ –8z + 14 = 12 + 2z
⇒ 14 – 12 = 8z + 2z
⇒ 10z = 2 ⇒ z = 2/10 = 1/5
Now, substituting the value of z back in equation (1), we get 2x = -4z + 7
⇒ x = -4/5 +7 = 31/10
∴The point R (31/10, 0, 1/5) in xz-plane is equidistant from A, B and C.
Question 5. Determine the point on z-axis which is equidistant from the points (1, 5, 7) and (5, 1, -4)
Solution:
Given: The points (1, 5, 7) and (5, 1, -4)
We know x = 0 and y = 0 on z-axis. Let R(0, 0, z) any point on z-axis
According to the question: RA = RB
⇒ RA2 = RB2
By using the formula, the distance between any two points (a, b, c) and (d, e, f) is given by,

We know, RA2 = RB2
⇒ 26+ (z – 7)2 = (z + 4)2 + 26
⇒ z2+ 49 – 14z + 26 = z2+ 16 + 8z + 26
⇒ 49 – 14z = 16 + 8z
⇒ 49 – 16 = 14z + 8z
⇒ 22z = 33
⇒ z = 33/22
⇒ z= 3/2
∴The point R (0, 0, 3/2) on z-axis is equidistant from (1, 5, 7) and (5, 1, -4).
Question 6. Find the point on y-axis which is equidistant from the points (3, 1, 2) and (5, 5, 2).
Solution:
Given: The points (3, 1, 2) and (5, 5, 2)
We know x = 0 and z = 0 on y-axis. Let R(0, y, 0) any point on the y-axis
According to the question: RA = RB
⇒ RA2 = RB2
By using the formula, the distance between any two points (a, b, c) and (d, e, f) is given by,

We know, RA2 = RB2
⇒ 13+ (y – 1)2 = (y – 5)2 + 29
⇒ y2+ 1 – 2y + 13 = y2+ 25 – 10y + 29
⇒ 10y – 2y = 54 – 14
⇒ 8y = 40
⇒ y = 40/8 = 5
∴The point R (0, 5, 0) on y-axis is equidistant from (3, 1, 2) and (5, 5, 2).
Question 7. Find the points on z-axis which are at a distance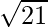 from the point (1, 2, 3).
from the point (1, 2, 3).
Solution:
Given: The point (1, 2, 3) and Distance =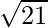
We know x = 0 and y = 0 on z-axis. Let R(0, 0, z) any point on z-axis
According to question:
RA =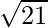
⇒ RA2 = 21
By using the formula, the distance between any two points (a, b, c) and (d, e, f) is given by,

RD Sharma Solutions for Class 11 Maths Chapter 28 – image 25
We know, RA2 = 21
⇒ 5 + (z – 3)2 = 21
⇒ z2+ 9 – 6z + 5 = 21
⇒ z2 – 6z = 21 – 14
⇒ z2– 6z – 7 = 0
⇒z2 – 7z + z – 7 = 0
⇒ z(z– 7) + 1(z – 7) = 0
⇒ (z– 7) (z + 1) = 0
⇒ (z– 7) = 0 or (z + 1) = 0
⇒ z= 7 or z = -1
∴The points (0, 0, 7) and (0, 0, -1) on z-axis is equidistant from (1, 2, 3).
Question 8. Prove that the triangle formed by joining the three points whose coordinates are (1, 2, 3), (2, 3, 1), and (3, 1, 2) is an equilateral triangle.
Solution:
Given: The points A(1, 2, 3), B(2, 3, 1) and C(3, 1, 2)
We know an equilateral triangle is a triangle whose all sides are equal.
So let us prove AB = BC = AC.
By using the formula, the distance between any two points (a, b, c) and (d, e, f) is given by,

So, distance between A(1, 2, 3) and B(2, 3, 1) is given by:
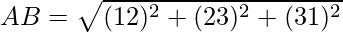
⇒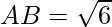
Distance between B(2, 3, 1) and C(3, 1, 2) is given by:
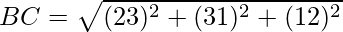
⇒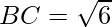
Distance between A(1, 2, 3) and C(3, 1, 2) is given by:
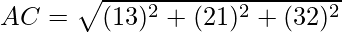
⇒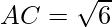
It is clear that, AB = BC = AC =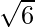
Δ ABC is a equilateral triangle.
Question 9. Show that the points (0, 7, 10), (-1, 6, 6), and (-4, 9, 6) are the vertices of an isosceles right-angled triangle.
Solution:
Given: The points A(0, 7, 10), B(-1, 6, 6) and C(-4, 9, 6).
By using the formula, the distance between any two points (a, b, c) and (d, e, f) is given by,

AB =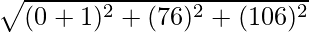
⇒ AB =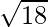
⇒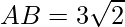
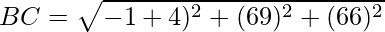
⇒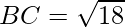
⇒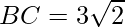
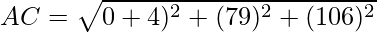
⇒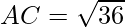
⇒ AC = 6
Since, AB = BC
So, AB2 + BC2 =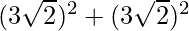
= 18 + 18 = 36
⇒ AB2 + BC2 = AC2
We know that, AB = BC and AB2 + BC2 = AC2
So, Δ ABC is an isosceles-right angled triangle.
Question 10. Show that points A(3, 3, 3), B(0, 6, 3), C(1, 7, 7) and D(4, 4, 7) are the vertices of squares.
Solution:
Given: The points A (3, 3, 3), B (0, 6, 3), C (1, 7, 7) and D (4, 4, 7)
We know that all sides of a square are equal.
By using the formula, the distance between any two points (a, b, c) and (d, e, f) is given by,

⇒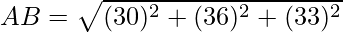
=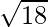
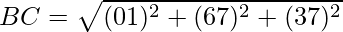
=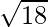
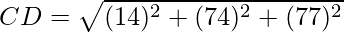
=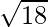
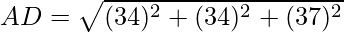
=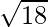
It is clear that, AB = BC = CD = AD =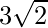
Quadrilateral formed by ABCD is a square. [Since all sides are equal]
Question 11. Prove that the point A(1, 3, 0), B(-5, 5, 2), C(-9, -1, 2) and D(-3, -3, 0) taken in order are the vertices of a parallelogram. Also, show that ABCD is not a rectangle.
Solution:
Given: The points A (1, 3, 0), B (-5, 5, 2), C (-9, -1, 2) and D (-3, -3, 0)
We know that, opposite sides of both parallelogram and rectangle are equal.
But diagonals of a parallelogram are not equal whereas they are equal for rectangle.
By using the formula, the distance between any two points (a, b, c) and (d, e, f) is given by,

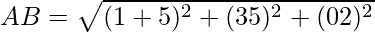
=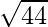
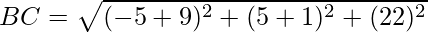
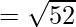
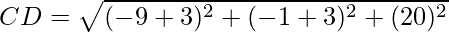
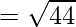
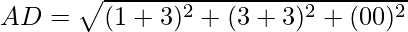
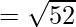
It is clear that, AB = CD and BC = AD
Opposite sides are equal. Now, let us find the length of diagonals
By using the formula,
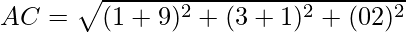
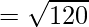
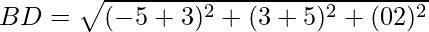
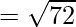
It is clear that, AC ≠ BD
The diagonals are not equal, but opposite sides are equal.
So we can say that quadrilateral formed by ABCD is a parallelogram but not a rectangle.
Question 12. Show that points A(1, 3, 4), B(-1, 6, 10), C(-7, 4, 7), and D(-5, 1, 1) are the vertices of a rhombus.
Solution:
Given: The points A (1, 3, 4), B (-1, 6, 10), C (-7, 4, 7) and D (-5, 1, 1)
We know that, all sides of both square and rhombus are equal.
By using the formula, the distance between any two points (a, b, c) and (d, e, f) is given by,

AB =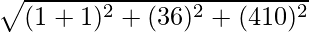
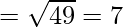
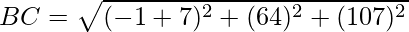
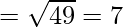
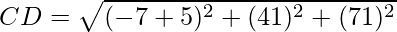
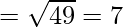
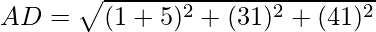
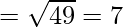
It is clear that, AB = BC = CD = AD
So, all sides are equal.
Now, let us find the length of diagonals. By using the formula,
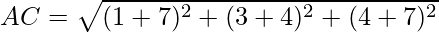
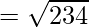
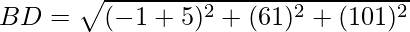
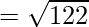
It is clear that, AC ≠ BD
The diagonals are not equal, but all sides are equal.
So we can say that quadrilateral formed by ABCD is a rhombus.
Share your thoughts in the comments
Please Login to comment...