Derivatives of Polynomial Functions
Last Updated :
26 Feb, 2024
Derivatives are used in Calculus to measure the rate of change of a function with respect to a variable. The use of derivatives is very important in Mathematics. It is used to solve many problems in mathematics like to find out maxima or minima of a function, slope of a function, to tell whether a function is increasing or decreasing. If a function is written as y = f(x) and we want to find the derivative of this function then it will be written as dy/dx and can be pronounced as the rate of change of y with respect to x.
The derivative of a polynomial function
To calculate the derivative of a polynomial function, first, you should know the product rule of derivatives and the basic rule of the derivative.
Product rule of derivative
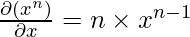
(Here n can be either positive or negative value)
Understand in this way: The old power of the variable is multiplied with the coefficient of the variable and the new power of the variable is decreased by 1 from the old power.
Example: Find the derivative of x3?
Solution:
Let y = x3
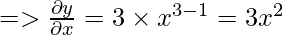
Some basic rules of derivative
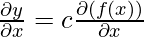
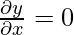
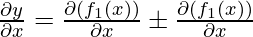
Example 1: Find the derivative of 4x3 + 7x?
Solution:
Let y = 4x3 + 7x
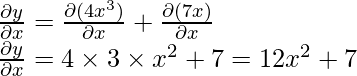
Example 2: Find the derivative of 3x2 – 7?
Solution:
Let y = 3x2 – 7
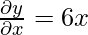
Some more examples on derivative of polynomials
Example 1: Find the derivative of 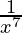 ?
?
Solution:
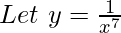
This can be written as
y = x−7
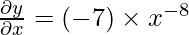
Example 2: Find the derivative of 7x5 + x3 − x?
Solution:
Let y = 7x5 + x3 − x
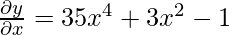
Example 3: Find the derivative of (x + 5)2 + 6x3 − 4?
Solution:
Let y = (x + 5)2 + 6x3 − 4
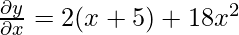
Example 4: Find the derivative of 6x3 + (6x + 5)2 − 8x?
Solution:
Let y = 6x3 + (6x + 5)2 − 8x
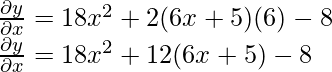
Example 5: Find the derivative of 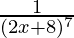 ?
?
Solution:
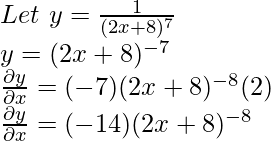
Share your thoughts in the comments
Please Login to comment...