Theorem 1: The number of permutations of n different objects taken r at a time, where 0 < r ≤ n and the objects do not repeat is
n(n-1)(n – 2). . .(n – r + 1), which is denoted by nPr = 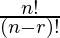
Theorem 2: The number of permutations of n different objects taken r at a time, where repetition is allowed, is nr.
Theorem 3: The number of permutations of n objects, where p objects are of the same kind and rest are all different
= 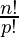
Theorem 4: The number of permutations of n objects, where P1 objects are of one kind, P2 are of second kind, …, Pk are of kth kind and the rest, if any, are of different kind is
= 
Question 1. How many 3-digit numbers can be formed by using the digits 1 to 9 if no digit is repeated?
Solution:
As we see here, we have given 9 different digits, and we have to select 3 out of them to form a three-digit number, and repetition is not allowed.

So according to Theorem 1: Therefore, there will be as many 3-digit numbers as there are permutations of 9 different digits taken 3 at a time.
= 9P3
= 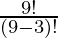
= 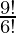
= 9×8×7
= 504
Hence, we can form 504 three-digit numbers.
Alternative solution: Multiplication Theorem
As in this case, repetition is not allowed. Here if unit place is filled first, it can be filled by any of the given nine digits. So, the number of ways of filling the units place of the three-digit number is 9.
Then, the tens place can be filled with any of the remaining eight digits and the hundreds place can be filled with any of the remaining seven digits.
Hence, by multiplication principle, the number of ways in which three-digit numbers can be formed without repeating are:
= 9×8×7
= 504
Question 2. How many 4-digit numbers are there with no digit repeated?
Solution:
As we know, we have 10 different digits (0, 1, 2, 3, 4, 5, 6, 7, 8 and 9) and we have to select 4 out of them to form a four-digit number, and repetition is not allowed.
BUT as we know we cannot place 0 at thousands place (because then number won’t be a four-digit number). So we will calculate permutation of remaining three place separately and thousands place separately.
For thousands place: we have 9 different digits (excluding 0) and we have to select 1 out of them.
and, For remaining three places: we have remaining 9 different digits (including 0) and we have to select 3 out of them.

So according to Theorem 1: Therefore, there will be as many 4-digit numbers as there are permutations of (9 different digits taken 1 at a time) and (9 different digits taken 3 at a time).
= 9P1 × 9P3
= 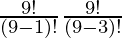
= 
= 9×9×8×7
= 4536
Hence, we can form 4536 four-digit numbers.
Alternative solution: Multiplication Theorem
As in this case, repetition is not allowed. Here the thousands place of the 4-digit number is to be filled first with any of the digits from 1 to 9 (0 cannot be included), Therefore the number of ways in which thousands place can be filled is 9.
Then, the hundreds place can be filled with any of the digits from 0 to 9. As the digit cannot be repeated in the 4-digit numbers and thousands place is already occupied with a digit. Then these remaining places is to be filled by remaining 9 digits.
Then, the tens place can be filled with any of the remaining eight digits and the hundreds place can be filled with any of the remaining seven digits.
Hence, by multiplication principle, the number of ways in which three-digit numbers can be formed without repeating are:
= 9×9×8×7
= 4536
Question 3. How many 3-digit even numbers can be made using the digits 1, 2, 3, 4, 6, 7 if no digit is repeated?
Solution:
As we know, we have 6 different digits (1, 2, 3, 4, 6 and 7) and we have to select 3 out of them to form a three-digit number, and repetition is not allowed.
BUT as we know we have to place a even number at ones place (because then number should be a even three-digit number). So we will calculate permutation of remaining two place separately and ones place separately.
For ones place: we have 3 different digits, and we have to select 1 out of them.
and, For remaining two places: we have remaining 5 different digits, and we have to select 2 out of them.

So according to Theorem 1: Therefore, there will be as many 3-digit even numbers as there are permutations of (3 different digits taken 1 at a time) and (5 different digits taken 2 at a time).
= 3P1 × 5P2
= 
= 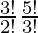
= 3×5×4
= 60
Hence, we can form 60 three-digit numbers.
Alternative solution: Multiplication Theorem
As in this case, repetition is not allowed. Here the ones place of the 3-digit number is to be filled first with any even number of the digits from 2, 4 and 6 (number will be even having end with 2, 4 and 6 ) , Therefore the number of ways in which ones place can be filled is 3.
Then, the tens and hundreds places can be filled with any of the remaining digits. As the digit cannot be repeated in the 3-digit numbers and ones place is already occupied with a digit. Then tens and hundreds remaining places is to be filled by remaining 5 and 4 digits respectively.
Hence, by multiplication principle, the number of ways in which three-digit numbers can be formed without repeating are:
= 3×5×4
= 60
Question 4. Find the number of 4-digit numbers that can be formed using the digits 1, 2, 3, 4, 5 if no digit is repeated. How many of these will be even?
Solution:
As we see here, we have given 5 different digits, and we have to select 4 out of them to form a four-digit number, and repetition is not allowed.

So according to Theorem 1: Therefore, there will be as many 4-digit numbers as there are permutations of 5 different digits taken 4 at a time.
= 5P4
= 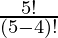
= 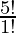
= 5×4×3×2×1
= 120
Hence, we can form 120 four-digit numbers.
For Even numbers?
As we know, we have 5 different digits (1, 2, 3, 4 and 5) and we have to select 4 out of them to form a four-digit number, and repetition is not allowed.
BUT as we know we have to place a even number at ones place (because then number should be a even four-digit number). So we will calculate permutation of remaining three places and ones place separately.
For ones place: we have 2 different digits, and we have to select 1 out of them.
and, For remaining three places: we have remaining 4 different digits, and we have to select 3 out of them.
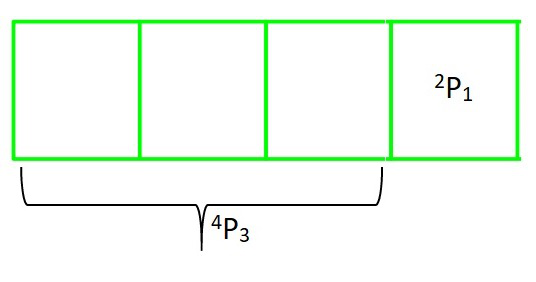
So according to Theorem 1: Therefore, there will be as many 4-digit even numbers as there are permutations of (2 different digits taken 1 at a time) and (4 different digits taken 3 at a time).
= 2P1 × 4P3
= 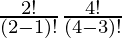
= 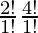
= 2×4×3×2
= 48
Hence, we can form 48 four-digit even numbers
Alternative solution: Multiplication Theorem
As in this case, repetition is not allowed. Here the ones place of the 4-digit number is to be filled first with any number of the digits from 1 to 5, Therefore the number of ways in which ones place can be filled is 5.
Then, the tens, hundreds and hundreds places can be filled with any of the remaining digits. As the digit cannot be repeated in the 4-digit numbers and ones place is already occupied with a digit. Then tens, hundreds and thousands remaining places is to be filled by remaining 4, 3 and 2 digits respectively.
Hence, by multiplication principle, the number of ways in which four-digit numbers can be formed without repeating are :
= 5×4×3×2
= 120
For Even numbers?
As in this case, repetition is not allowed. Here the ones place of the 4-digit number is to be filled first with any even number of the digits from 2 and 4(number will be even having end with 2 and 4), Therefore the number of ways in which ones place can be filled is 2.
Then, the tens, hundreds and hundreds places can be filled with any of the remaining digits. As the digit cannot be repeated in the 4-digit numbers and ones place is already occupied with a digit. Then tens, hundreds and thousands remaining places is to be filled by remaining 4, 3 and 2 digits respectively.
Hence, by multiplication principle, the number of ways in which four-digit even numbers can be formed without repeating are :
= 2×4×3×2
= 48
Question 5. From a committee of 8 persons, in how many ways can we choose a chairman and a vice-chairman assuming one person can not hold more than one position?
Solution:
As we see here, There are 8 different people, and we have to select 2 out of them to form a committee and repetition is not allowed (one person can not hold more than one position).

So according to Theorem 1: Therefore, there will be as many committee can be formed as there are permutations of 8 people taken 2 at a time.
= 8P2
=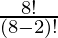
= 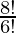
= 8×7
= 56
Hence, we can form 56 committee of two people.
Alternative solution: Multiplication Theorem
As in this case, one person can not hold more than one position. Here if we choose first person, So, the number of ways we have is 8.
Then, if we choose second person, as first person is already selected So, the number of ways we have is 7.
Hence, by multiplication principle, the number of ways in which a committee of two people can be formed:
= 8×7
= 56
Question 6. Find n if, n –1P3: nP4 = 1 : 9.
Solution:
Given.
n –1P3 / nP4 = 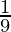 ………………………………….(1)
………………………………….(1)
as nPr = 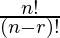
n –1P3 / nP4 = 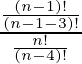
= 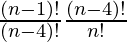 (cancelling (n-4)!))
(cancelling (n-4)!))
= 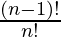
= 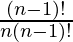 (n! = n × (n-1)!)
(n! = n × (n-1)!)
= 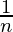 (cancelling (n-1)!))
(cancelling (n-1)!))
On simplification (1) we get,

Hence, n = 9
Question 7. Find r if
(i) 5Pr = 2 6Pr−1
(ii) 5Pr = 6Pr−1
Solution:
(i) Given.
5Pr = 2 6Pr−1
as nPr = 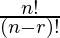
So,
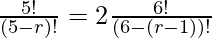
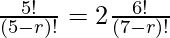
By shifting (7-r)! to the LHS and 5! to the RHS we get,
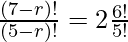
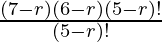 = 2 (6) ((7-r)! = (7-r) (7-r-1) (7-r-2)! = (7-r) (6-r) (5-r)!
= 2 (6) ((7-r)! = (7-r) (7-r-1) (7-r-2)! = (7-r) (6-r) (5-r)!
(7-r) (6-r) = 2 (6) ………………………(1) (cancelling (5-r)!))
On simplification (1) we get,
42-6r- 7r+r2 = 12
r2-13r+30=0
r2-10r-3r+30=0
r(r-10)-3(r-10) = 0
(r-3) (r-10) = 0
Then r=3 and r=10
in nPr, r is always 0<r≤n
So here, 0<r≤5
r=3 and r≠10
Hence, r=3
(ii) Given.
5Pr = 6Pr−1
as nPr = 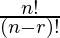
So,
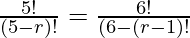
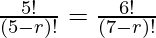
By shifting (7-r)! to the LHS and 5! to the RHS we get,
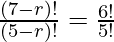
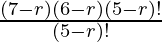 = 6 ((7-r)! = (7-r) (7-r-1) (7-r-2)! = (7-r) (6-r) (5-r)!
= 6 ((7-r)! = (7-r) (7-r-1) (7-r-2)! = (7-r) (6-r) (5-r)!
(7-r) (6-r) = 6) ………………………(1) (cancelling (5-r)!))
On simplification (1) we get,
42-6r- 7r+r2 = 6
r2-13r+36=0
r2-9r-4r+36=0
r(r-9)-4(r-9) = 0
(r-9) (r-4) = 0
Then r=9 and r=4
in nPr, r is always 0<r≤n
So here, 0<r≤5
r=4 and r≠9
Hence, r=4
Question 8. How many words, with or without meaning, can be formed using all the letters of the word EQUATION, using each letter exactly once?
Solution:
As we see here, There are 8 different letters, and we have to form 8 letter words using these letters and repetition is not allowed (using each letter exactly once).

So according to Theorem 1: Therefore, there will be permutations of 8 different letters taken 8 at a time.
= 8P8
= 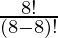
= 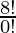
= 8!
= 8×7×6×5×4×3×2×1
= 40320
Hence, we can form 40320 words.
Question 9. How many words, with or without meaning can be made from the letters of the word MONDAY, assuming that no letter is repeated, if.
(i) 4 letters are used at a time,
(ii) all letters are used at a time,
(iii) all letters are used but first letter is a vowel?
Solution:
MONDAY has 6 different letters.

(i) As we see here, There are 6 different letters, and we have to form 4 letters word using these letters and repetition is not allowed.
So according to Theorem 1: Therefore, there will be permutations of 6 different letters taken 4 at a time.
= 6P4
= 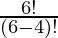
= 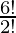
= 6×5×4×3
= 360
Hence, we can form 360 words.

(ii) As we see here, There are 6 different letters and we have to form 6 letters word using these letters and repetition is not allowed.
So according to Theorem 1: Therefore, there will be permutations of 6 different letters taken 6 at a time.
= 6P6
= 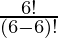
= 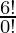
= 6×5×4×3×2×1
= 720
Hence, we can form 720 words.

(iii) As we know, we have 6 different letters and we have to select 6 out of them as all letters are used but first letter is a vowel, and repetition is not allowed.
BUT as we know we have to place a vowel at first place. So we will calculate permutation of remaining 5 places and 1 place separately.
For first place : we have 2 different letters, and we have to select 1 out of them.
and, For remaining places : we have remaining 5 different letters, and we have to select 5 out of them.
So according to Theorem 1: Therefore, there will be as many 6 letter word as there are permutations of (2 different letters taken 1 at a time) and (5 different letters taken 5 at a time).
= 2P1 × 5P5
= 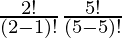
= 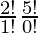
= 2×5×4×3×2×1
= 240
Hence, we can form 240 words.
Question 10. In how many of the distinct permutations of the letters in MISSISSIPPI do the four I’s not come together?
Solution:
MISSISSIPPI has 11 letters where,
So according to Theorem 4: Therefore, there will be as many 11 letter word as there are permutations of 11 letters taken 11 at a time having some repetition words.
= 11P11/(1! 4! 4! 2!)
= 
= 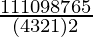 (cancelling 4!)
(cancelling 4!)
No. of distinct permutations of the letters = 34650
Now, as there are 4 I’s in the given word. When they occur together, they are treated as a single object for the time being.
Hence, total number of words = 11-4+1 = 8
So according to Theorem 4: Therefore, there will be as many 8 letter word as there are permutations of 8 letters taken 8 at a time having some repetition words.
= 8P8/(1! 4! 2!)
= 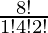
= 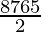 (cancelling 4!)
(cancelling 4!)
= 840
Hence, distinct permutations of the letters in MISSISSIPPI where four I’s not come together = 34650 – 840
= 33810
Question 11. In how many ways can the letters of the word PERMUTATIONS be arranged if the
(i) words start with P and end with S,
(ii) vowels are all together,
(iii) there are always 4 letters between P and S?
Solution:
PERMUTATIONS has 12 letters, where repetition of ‘T’ 2 times.

(i) First and last letter are fixed as P and S respectively.
then 12-2 = 10 letters are left.
So according to Theorem 4: Therefore, there will be as many 12 letter word as there are permutations of 10 letters taken 10 at a time having some repetition words.
= 10P10 /2!
= 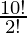
= 10×9×8×7×6×5×4×3
= 1814400
(ii) No. of vowels in PERMUTATIONS (E, U, A, I, O) = 5
Now considering all vowels together as one object.
Total number of letters = 12-5+1 = 8
So according to Theorem 4: Therefore, there will be as many 8 objects word as there are permutations of 8 objects taken 8 at a time having some repetition words.
= 8P8 /2!
= 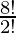
Using Multiplication principle, the number of arrangement of vowels will be:
=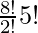
= 2419200
(iii) As there should be 4 letters between P and S.
So, two places for P and S are fixed.
then 12-2 = 10 letters are left.
So according to Theorem 4: Therefore, there will be as many 12 letter word as there are permutations of 10 letters taken 10 at a time having some repetition words.
= 10P10 /2!
= 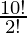
As there are 14 possible ways to place P and S between 4 letters.
Placing at (1 & 6), (6 & 1), (2 & 7), (7 & 2), (3 and 8), (8 & 3), (4 & 9) and (9 & 4), (5 & 10), (10 & 5), (11 & 6), (6 & 11), (12 & 7) and (7 & 12) position.
Hence, there are =  ×14
×14
= 25401600
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...