Class 11 NCERT Solutions- Chapter 10 Straight Lines – Exercise 10.2 | Set 1
Last Updated :
05 Apr, 2021
In Exercises 1 to 8, find the equation of the line which satisfy the given conditions:
Question 1. Write the equations for the x-and y-axes.
Solution:
The y-coordinate of every point on x-axis is 0 and the x-coordinate of every point on y-axis is 0
So, the equation of x-axis is y = 0 and the equation of y-axis is y = 0.
Question 2. Passing through the point (– 4, 3) with slope 1/2.
Solution:
Given that point p(x1, y1) is (-4, 3) and slope m = 1/2
Equation of Line can be derived by formula y – y1 = m (x – x1),
Where m is slope of line and (x1, y1) is co-ordinate of p from which line passes.
y – 3 = 1/2(x – (-4))
y – 3 = 1/2 (x + 4)
2(y – 3) = x + 4
2y – 6 = x + 4
x + 4 – (2y – 6) = 0
x + 4 – 2y + 6 = 0
x – 2y + 10 = 0
So, the equation of the line is x – 2y + 10 = 0.
Question 3. Passing through (0, 0) with slope m.
Solution:
Given that Point p(x1, y1) is (0, 0) and slope is m.
So, the equation of Line can be derived by formula y – y1 = m (x – x1),
Where m is slope of line and (x1, y1) is co-ordinate from which line passes.
So, y – 0 = m (x – 0)
y = mx
y – mx = 0
So, the equation of the line is y – mx = 0.
Question 4. Passing through (2, 2√3) and inclined with the x-axis at an angle of 75o.
Solution:
Given that point p(x1, y1) is (2, 2√3) and θ = 75°
So, the equation of line is (y – y1) = m (x – x1)
where, m = slope of line = tan θ and (x1, y1) are the points through which line passes
So, m = tan 75°
Now, finding tan 75° using below formula:
tan(A + B) = (tanA + tanB)/(1 – tanA.tanB)
tan 75° = tan(45° + 30°)
tan 75° = (tan 45° + tan 30°)/(1 – tan 30°.tan 45°)
tan 75° = (1 + 1/√3)/(1 – 1/√3)
tan 75° = (√3 + 1)/(√3 – 1)
By rationalizing, we get
tan 75° = 2 + √3
Equation of Line will be,
(y – 2√3) = (2 + √3)(x – 2)
y – 2√3 = 2 x – 4 + √3x – 2 √3
y = 2 x – 4 + √3x
(2 + √3)x – y – 4 = 0
So, the equation of the line is (2 + √3)x – y – 4 = 0.
Question 5. Intersecting the x-axis at a distance of 3 units to the left of origin with slope –2.
Solution:
Given that Slope m = –2, x-intercept = 3,
that means Line is passing from point p(x1, y1) that is (3, 0)
Equation of line will be
y – 0 = (–2) × (x − 3).
y = (–2) × (x + 3)
y = –2x – 6
2x + y + 6 = 0
So, the equation of the line is 2x + y + 6 = 0.
Question 6. Intersecting the y-axis at a distance of 2 units above the origin and making an angle of 30° with the positive direction of the x-axis.
Solution:
Given that θ = 30° then slope(m) will be = tan θ
m = tan30° = (1/√3)
As Y intercept is 2 that means line is passing from (0, 2) point p(x1, y1) = (0, 2)
Equation of Line will be
y – 2 = (1/√3)x
y = (1/√3)x + 2
y = (x + 2√3) / √3
√3 y = x + 2√3
x – √3 y + 2√3 = 0
So, the equation of the line is x – √3 y + 2√3 = 0.
Question 7. Passing through the points (–1, 1) and (2, – 4).
Solution:
Given that point p1(x1, y1) is (–1, 1) and point p2(x2, y2) is (2, –4),
It is mention in question that line passes from p1 and p2.
That means, the Slope(m) of line will be (y2 – y1)/(x2 – x1)
m = (–4 – 1)/(2 – (–1))
m = –5/3
Equation of Line will be
(y – y1) = m(x – x1)
y – 1 = –5/3 (x + 1)
3 (y – 1) = (–5)(x + 1)
3y – 3 = –5x – 5
3y – 3 + 5x + 5 = 0
5x + 3y + 2 = 0
So, the equation of the line is 5x + 3y + 2 = 0.
Question 8. Perpendicular distance from the origin is 5 units and the angle made by the perpendicular with the positive x-axis is 30°.
Solution:
Given that p = 5 and ω = 30°
We know that the equation of the line having normal distance p from the origin and
angle ω which the normal makes with the positive direction of x-axis is given by x cos ω + y sin ω = p.
On substituting the values in the equation, we get
x cos30° + y sin30° = 5
x(√3 / 2) + y(1/2) = 5
√3 x + y = 5(2) = 10
√3 x + y – 10 = 0
So, the equation of the line is √3 x + y – 10 = 0.
Question 9. The vertices of ΔPQR are P (2, 1), Q (–2, 3), and R (4, 5). Find the equation of the median through the vertex R.
Solution:
Given Vertices of ΔPQR that are P (2, 1), Q (–2, 3) and R (4, 5)
Let RS be the median of vertex R => S is a midpoint of PQ.
As S is midpoint of PQ => S = (P + Q)/2
S = (2 – 2, 1 + 3)/2
S = (0, 2)
Equation of the line passing through the points (x1, y1) and (x2, y2) is given by
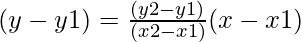
y – 5 = –3/ –4(x – 4)
(–4)(y – 5) = (–3)(x – 4)
–4y + 20 = –3x + 12
–4y + 20 + 3x – 12 = 0
3x – 4y + 8 = 0
So, the equation of median through the vertex R is 3x – 4y + 8 = 0.
Question 10. Find the equation of the line passing through (–3, 5) and perpendicular to the line through the points (2, 5) and (–3, 6).
Solution:
Given that Points are (2, 5) and (-3, 6).
So, the slope, m1 = (y2 – y1)/(x2 – x1)
= (6 – 5)/(–3 – 2)
= 1/–5 = –1/5
As we know that two non-vertical lines are perpendicular to each other
if their slopes are negative reciprocals of each other.
Then, m = (–1/m1)
= –1/(–1/5)
= 5
As we know that the point p(x, y) lies on the line with
slope m through the fixed point (x1, y1),
If its coordinates satisfy the equation y – y1 = m (x – x1)
Then, y – 5 = 5(x – (–3))
y – 5 = 5x + 15
5x + 15 – y + 5 = 0
5x – y + 20 = 0
So, the equation of the line is 5x – y + 20 = 0
Share your thoughts in the comments
Please Login to comment...