Class 11 RD Sharma solutions – Chapter 29 Limits – Exercise 29.7 | Set 1
Last Updated :
04 May, 2021
Question 1. Limx→0[sin3x/5x]
Solution:
We have,
Limx→0[sin3x/5x]
= (1/5)Limx→0[sin3x/3x] × 3
= (3/5)Limx→0[sin3x/3x]
As we know that, Limx→0[sinx/x] = 1
= (3/5)
Question 2. Limx→0[sinx°/x]
Solution:
We have,
Limx→0[sinx°/x]
As we know that x° = [(πx)/180]
= Limx→0[sin{(πx)/180}/x]
= 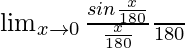
= (π/180) × 1
= (π/180)
Question 3. Limx→0[x2/sinx2]
Solution:
We have,
Limx→0[x2/sinx2]
=![Rendered by QuickLaTeX.com Lim_{x→0}[\frac{1}{\frac{sinx^2}{x^2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-51360b1c365eea197f4c0e8281a1cc9d_l3.png)
= ![Rendered by QuickLaTeX.com [\frac{1}{ Lim_{x→0}\frac{sinx^2}{x^2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-576347cf724959c6e5bfbc6fd981d749_l3.png)
As we know that, Limx→0[sinx/x] = 1
= 1/1
= 1
Question 4. Limx→0[sinx.cosx/3x]
Solution:
We have,
Limx→0[(sinx.cosx)/3x]
= Limx→0[(sinx.cosx)/ × 3x]
= 1/3 Limx→0[(sinx)/x] × Limx→0[(cosx)]
As we know that Limx→0[sinx/x] = 1, and Limx→0cos0 = 1
= (1/3) × 1 × 1
= 1/3
Question 5. Limx→0[(3sinx – 4sin3x)/x]
Solution:
We have,
Limx→0[(3sinx – 4sin3x)/x]
As we know that 3sinx – 4sin3x = sin3x
= Limx→0[(sin3x)/3x] × 3
= 3 × Limx→0[(sin3x)/3x]
As we know that, Limx→0[sinx/x] = 1
= 3 × 1
= 3
Question 6. Limx→0[tan8x/sin2x]
Solution:
We have,
Limx→0[tan8x/sin2x]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{tan8x}{8x}×8x][\frac{1}{\frac{sin2x}{2x}×2x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f317aa065bc84455e39336fcad15b855_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{tan8x}{8x}][\frac{1}{\frac{sin2x}{2x}}]×\frac{8x}{2x}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-be3317ba30efaabf8a6832da8271209b_l3.png)
As we know that Limx→0[sin2x/2x] = 1 and Limx→0[tan8x/8x] = 1
= 8/2
= 4
Question 7. Limx→0[tan(mx)/tan(nx)]
Solution:
We have,
Limx→0[tan(mx)/tan(nx)]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{tanmx}{mx}×mx][\frac{1}{\frac{tannx}{nx}×nx}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dccab1c629408c5b0f4564abc866be52_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{tanmx}{mx}][\frac{1}{\frac{tannx}{nx}}]×\frac{mx}{nx}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-14f223f5c417b6ae20a5187c184248b7_l3.png)
As we know that Limx→0[tanx/x] = 1
= m × 1/n × 1
= m/n
Question 8. Limx→0[sin5x/tan3x]
Solution:
We have,
Limx→0[sin5x/tan3x]
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{sin5x}{5x}×5x][\frac{1}{\frac{tan3x}{3x}×3x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a4954271c9713bf932bb9621f07c6863_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{sin5x}{5x}][\frac{1}{\frac{tan3x}{3x}}]×\frac{5x}{3x}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2c6ed918b58745302694bbaeeb61232a_l3.png)
As we know that Limx→0[sin5x/5x] = 1 and Limx→0[tan3x/3x] = 1
= 5/3 × 1
= 5/3
Question 9. Limx→0[sin(xn)/(xn)]
Solution:
We have,
Limx→0[sin(xn)/(xn)]
It is in the form of 0/0
So, let xn = y
x→0 than y→0
Limy→0[siny/y]
As we know that Limy→0[siny/y] = 1
= 1
Question 10. Limx→0[(7xcosx – 3sinx)/(4x + tanx)]
Solution:
We have,
Limx→0[(7xcosx – 3sinx)/(4x + tanx)]
= Limx→0[x(7cosx-3sinx/x)/x(4 + tanx/x)]
= Limx→0[(7cosx-3sinx/x)/(4 + tanx/x)]
= 
As we know that Limx→0[sinx/x] = 1 and Limx→0[tanx/x] = 1
= (7 – 3)/(4 + 1)
= 4/5
Question 11. Limx→0[{cos(ax) – cos(bx)}/{cos(cx) – cos(dx)}]
Solution:
We have,
Limx→0[{cos(ax) – cos(bx)}/{cos(cx) – cos(dx)}]
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{-2sin(\frac{ax+bx}{2})sin(\frac{ax-bx}{2})}{-2sin(\frac{cx+dx}{2})sin(\frac{cx-dx}{2})}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-528b21a544687f5647e22c3fb02d7f87_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{\frac{sin(\frac{ax+bx}{2})}{(\frac{ax+bx}{2})}×(\frac{ax+bx}{2})\frac{sin(\frac{ax-bx}{2})}{(\frac{ax-bx}{2})}×(\frac{ax-bx}{2})}{\frac{sin(\frac{cx+dx}{2})}{(\frac{cx+dx}{2})}×(\frac{cx+dx}{2})\frac{sin(\frac{cx-dx}{2})}{(\frac{cx-dx}{2})}×(\frac{cx-dx}{2})}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7251dec0699ffd24b5032194ba3a05af_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{\frac{(ax+bx)}{2}\frac{(ax-bx)}{2}}{\frac{(cx+dx)}{2}\frac{(cx-dx)}{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-56cfc094221708a097d62962bd6531da_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{x^2(a+b)(a-b)}{x^2(c+d)(c-d)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b9c5d622a36a1aa226939c3ec1b100d6_l3.png)
= (a2 – b2)/(c2 – d2)
Question 12. Limx→0[(tan23x)/x2]
Solution:
We have,
Limx→0[(tan23x)/x2]
= Limx→0[(tan3x)/x]2
= Limx→0[(tan3x)/3x]2 × 9
As we know that Limx→0[tanx/x] = 1
= 1 × 9
= 9
Question 13. Limx→0[(1 – cosmx)/x2]
Solution:
We have,
Limx→0[(1 – cosmx)/x2]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{2sin^2\frac{mx}{2}}{x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-66be28dfd809b7d6490be21fd965fec0_l3.png)
= ![Rendered by QuickLaTeX.com 2\lim_{x\to0}[\frac{sin\frac{mx}{2}}{x}]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bd0e4bb4344f6fea385138530ba03e04_l3.png)
= ![Rendered by QuickLaTeX.com 2\lim_{x\to0}[\frac{sin\frac{mx}{2}}{\frac{mx}{2}}]^2×(\frac{m}{2})^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b7c8bcafa2a76338b130fdfa798b9b83_l3.png)
As we know that Limx→0[sinx/x] = 1
= 2 × (m/2)2
= m2/2
Question 14. Limx→0[(3sin2x + 2x)/(3x + 2tan3x)]
Solution:
We have,
Limx→0[(3sin2x + 2x)/(3x + 2tan3x)]
= Limx→0[2x(1 + 3sin2x/2x)/3 x (1 + 2tan3x/3x)]
= (2/3)Limx→0[(1 + 3sin2x/2x)/3 x (1 + 2tan3x/3x)]
=
As we know that Limx→0[sinx/x] = 1 and Limx→0[tanx/x] = 1
= (2/3) × (4/3)
= 8/9
Question 15. Limx→0[(cos3x – cos7x)/x2]
Solution:
We have,
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{-2sin(\frac{3x+7x}{2})sin(\frac{3x-7x}{2})}{x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d3d9ab6e2170f9e04208f1289ef71163_l3.png)
= Limx→0[-2sin5x.sin(-2x)/x2]
= Limx→0[2sin5x.sin2x/x2]
= ![Rendered by QuickLaTeX.com 2\lim_{x\to0}[\frac{sin5x}{5x}×5]×\lim_{x\to0}[\frac{sin2x}{2x}×2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3e6a6c790cd5eb40fd995f1b931855f8_l3.png)
As we know that Limx→0[sinx/x] = 1
= 2 × 5 × 2
= 20
Question 16. Limθ→0[sin3θ/tan2θ]
Solution:
We have,
Limθ→0[sin3θ/tan2θ]
= ![Rendered by QuickLaTeX.com \lim_{θ\to0}[\frac{sin3θ}{3θ}×3θ][\frac{1}{\frac{tan2θ}{2θ}×2θ}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7dc26374bdb9f25c167b24ff01912c01_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{sin3θ}{3θ}][\frac{1}{\frac{tan2θ}{2θ}}]×\frac{3θ}{2θ}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-172bae105eba45274da8a0527b862373_l3.png)
As we know that Limx→0[sinx/x] = 1 and Limx→0[tanx/x] = 1
= 3/2
Question 17. Limx→0[sinx2(1 – cosx2)/x6]
Solution:
We have,
Limx→0[sinx2(1 – cosx2)/x6]
= Limx→0[sinx2{2sin(x2/2}/x6]
= ![Rendered by QuickLaTeX.com 2\lim_{x\to0}[\frac{sinx^2.sin^2(\frac{x^2}{2})}{x^6}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8b6e7ce010647b22bba7c979a707530d_l3.png)
= 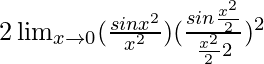
= 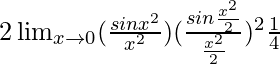
As we know that Limx→0[sinx/x] = 1
= 2 × (1/4)
= 1/2
Question 18. Limx→0[sin2(4x2)/x4]
Solution:
We have,
Limx→0[sin2(4x2)/x4]
= Limx→0[(sin(4x2))2/(x2)2]
= Limx→0[sin(4x2)/4x2]2 × 42
As we know that Limx→0[sinx/x] = 1
= 42
= 16
Question 19. Limx→0[(xcosx + 2sinx)/(x2 + tanx)]
Solution:
We have,
Limx→0[(xcosx + 2sinx)/(x2 + tanx)]
= Limx→0[x(cosx + 2sinx/x)/x(x + tanx/x)]
= Limx→0[(cosx + 2sinx/x)/(x + tanx/x)]
=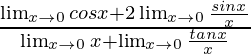
As we know that Limx→0[sinx/x] = 1 and Limx→0[tanx/x] = 1
= (1 + 2)/(0 + 1)
= 3
Question 20. Limx→0[(2x – sinx)/(x + tanx)]
Solution:
We have,
Limx→0[(2x – sinx)/(x + tanx)]
= Limx→0[x(2 – sinx/x)/x(1 + tanx/x)]
= Limx→0[(2 – sinx/x)/(1 + tanx/x)]
= 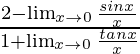
As we know that Limx→0[sinx/x] = 1 and Limx→0[tanx/x] = 1
= (2 – 1)/(1 + 1)
= 1/2
Question 21. Limx→0[(5xcosx + 3sinx)/(3x2 + tanx)]
Solution:
We have,
Limx→0[(5xcosx + 3sinx)/(3x2 + tanx)]
= Limx→0[x(5cosx + 3sinx/x)/x(3x + tanx/x)]
= Limx→0[(5cosx + 3sinx/x)/(3x + tanx/x)]
= 
As we know that Limx→0[sinx/x] = 1 and Limx→0[tanx/x] = 1
= (5 cos0 + 3)/(0 + 1)
= 8
Question 22. Limx→0[(sin3x – sinx)/(sinx)]
Solution:
We have,
Limx→0[(sin3x – sinx)/(sinx)]
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{2cos(\frac{3x+x}{2})sin(\frac{3x-x}{2})}{sinx}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3f695ce403efc742301500b29b0d5464_l3.png)
= 2Limx→0[cos2x.sinx/sinx]
= 2Limx→0cos2x
= 2 × cos0
= 2 × 1
= 2
Question 23. Limx→0[(sin5x – sin3x)/(sinx)]
Solution:
We have,
Limx→0[(sin5x – sin3x)/(sinx)]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{2cos(\frac{5x+3x}{2})sin(\frac{5x-3x}{2})}{sinx}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a3ed5c1e2d99b820aa4d1a0249b9d1c0_l3.png)
= 2Limx→0[cos4x.sinx/sinx]
= 2Limx→0cos4x
= 2 × cos0
= 2 × 1
= 2
Question 24. Limx→0[(cos3x – cos5x)/x2]
Solution:
We have,
Limx→0[(cos3x – cos5x)/x2]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{-2sin(\frac{3x+5x}{2})sin(\frac{3x-5x}{2})}{x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7674b35e73b62666475466566c48d5a3_l3.png)
= Limx→0[-2sin4x.sin(-x)/x2]
= Limx→0[2sin4x.sinx/x2]
= ![Rendered by QuickLaTeX.com 2\lim_{x\to0}[\frac{sin4x}{4x}×4]×\lim_{x\to0}[\frac{sinx}{x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-24f672d1f075b9484e1accf81b1b02df_l3.png)
As we know that Limx→0[sinx/x] = 1
= 2 × 4 × 1
= 8
Question 25. Limx→0[(tan3x – 3x)/(3x – sin2x)]
Solution:
We have,
Limx→0[(tan3x – 3x)/(3x – sin2x)]
= Limx→0[x(tan3x/x – 3)/x(3 – sin2x/x)]
= Limx→0[(tan3x/x – 3)/(3 – sin2x/x)]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{\frac{tan3x}{3x}×3-2}{3-\frac{sinx}{x}×sinx}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f55a3177015759a92111248b900083bd_l3.png)
As we know that Limx→0[sinx/x] = 1
= (3 – 2)/(3 – 0)
= 1/3
Question 26. Limx→0[{sin(2 + x) – sin(2 – x)}/x]
Solution:
We have,
Limx→0[{sin(2 + x) – sin(2 – x)}/x]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{2cos(\frac{2+x+2-x}{2})sin(\frac{2+x-2+x}{2})}{x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2436bdb37b42c483d94903a3e8ecfc1f_l3.png)
= 2Limx→0[cos2.sinx/x]
= 2cos×2Limx→0[sinx/x]
As we know that Limx→0[sinx/x] = 1
= 2cos2
Question 27. Limh→0[{(a + h)2sin(a + h) – a2sina}/h]
Solution:
We have,
Limh→0[{(a + h)2sin(a + h) – a2sina}/h]
= Limh→0[{a2sin(a + h) + h2sin(a + h) + 2ahsin(a + h) – a2sina}/h]
= ![Rendered by QuickLaTeX.com \lim_{h\to0}[a^2(\frac{sin(a+h)-sina}{h}+\frac{h^2sin(a+h)}{h}+\frac{2ahsin(a+h)}{h}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-11e81232df4a3938cfc3ce62be559539_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{h\to0}[a^2\frac{2cos\frac{(a+h+a)}{2}sin\frac{(a+h-a)}{2}}{2×\frac{h}{2}}+hsin(a+h)+2asin(a+h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fd5d962e38cc9c0b0e21144a86b0218b_l3.png)
= 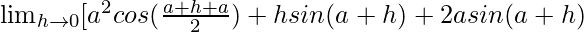
= a2cosa + 0 + 2asina
= a2cosa + 2asina
Question 28. Limx→0[{tanx – sinx}/{sin3x – 3sinx}]
Solution:
We have,
Limx→0[{tanx – sinx}/{sin3x – 3sinx}]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{\frac{sinx}{cosx}-sinx}{3sinx-4sin^3x-3sinx}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c9dd75992d3b99f7389ea715afd944aa_l3.png)
= ![Rendered by QuickLaTeX.com \frac{-1}{4}\lim_{x\to0}[\frac{sinx(\frac{1}{cosx}-1)}{sin^2x.sinx}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-29517b866535bb84678ea7cfa98c07ac_l3.png)
= ![Rendered by QuickLaTeX.com \frac{-1}{4}\lim_{x\to0}[\frac{(\frac{1-cosx}{cosx})}{1-cos^2x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-48d0c166ebe6cf26c3e0f923684b3bdd_l3.png)
= ![Rendered by QuickLaTeX.com \frac{-1}{4}\lim_{x\to0}[\frac{(1-cosx)}{cosx(1-cosx)(1+cosx)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-60203ad8993c082bacfa7495bb3e0c62_l3.png)
= ![Rendered by QuickLaTeX.com \frac{-1}{4}\lim_{x\to0}[\frac{1}{cosx(1+cosx)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3fb6aa60f7756ad508e00b315dfb5de0_l3.png)
= (-1/4)(1/2)
= -(1/8)
Question 29. Limx→0[{sex5x – sec5x}/{sec3x – secx}]
Solution:
We have,
Limx→0[{sex5x – sec5x}/{sec3x – secx}]
= 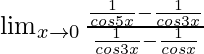
= 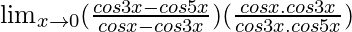
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{-2sin4x.sin(-x)}{-2sin2x.sin(-x)}][\frac{cosx}{cos5x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8c11b6e7b0ed29fd2461d22049d93c40_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{sin4x}{sin2x}][\frac{cosx}{cos5x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-756481495ab5928fc19f161f0e6969c2_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{\frac{sin4x}{4x}×4x}{\frac{sin2x}{2x}×2x}][\frac{cosx}{cos5x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-da050c618dedf8b53cbe3d4d9d97785e_l3.png)
As we know that Limx→0[sinx/x] = 1
= (4x/2x)(cos0/cos0)
= 2
Question 30. Limx→0[{1 – cos2x}/{cos2x – cos3x}]
Solution:
We have,
Limx→0[{1 – cos2x}/{cos2x – cos3x}]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{2sin^2x}{-2sin(\frac{3x+7x}{2})sin(\frac{3x-7x}{2})}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-88e36d1081dd924008f1c2a18047f21a_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{2sin^2x}{2sin(5x)sin(3x)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-073f91faa939f5db5b381dafa2596f34_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{sinx.sinx}{sin(5x)sin(3x)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-02c146902c645031f002e750ae42e98d_l3.png)
= 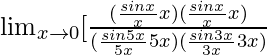
As we know that Limx→0[sinx/x] = 1
= (1/5 × 3)
= 1/15
Question 31. Limx→0[(1 – cos2x + tan2x)/(xsinx)]
Solution:
We have,
Limx→0[(1 – cos2x + tan2x)/(xsinx)]
= Limx→0[(2sin2x + tan2x)/(xsinx)]
Dividing numerator and denominator by x2
= 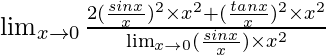
As we know that Limx→0[sinx/x] = 1 and Limx→0[tanx/x] = 1
= (2 × 1 × x2 + 1) + (1 × x2) /(1 × x2)
= 3
Share your thoughts in the comments
Please Login to comment...