Class 11 NCERT Solutions- Chapter 3 Trigonometric Function – Exercise 3.4
Last Updated :
03 Apr, 2024
Note: Please note that Exercise 3.4 from Chapter 3, “Trigonometric Function” in the NCERT Solutions, has been removed from the revised syllabus. As a result, this exercise will no longer be a part of your study curriculum.
Find the principal and general solutions of the following equations:
Question 1. tan x = √3
Solution:
Given: tan x = √3
Here, x lies in first or third quadrant.
∴ tanx = tan60°∘ or tanx = tan(180° + 60°)
tanx = tan60°∘ or tanx = tan240°∘
Here, the principal solutions are π/3, 4π/3.
∴ tanx = tanπ/3
⇒ x = nπ + π/3 where n ∈ Z
Question 2. sec x = 2
Solution:
Given: sec x = 2
It can be written as, cos x = 1/2
Here, x lies in first or fourth quadrant.
∴ cosx = cos60°∘ or cosx = cos(360° – 60°)
cosx = cos60°∘ or cosx = cos300°∘
cosx = cosπ/3 or cosx = cos 5π/3
Here, the principal solutions are π/3, 5 π/3
∴ cosx = cosπ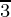
x = 2nπ ± π/3 where, n ∈ Z
Question 3. cot x = −√3
Solution:
Given: cot x = −√3
It can be written as, tan x = -1/√3
Here, x lies in second or fourth quadrant.
∴ tanx = −tan30°∘= tan(180°– 30°) or tanx = tan(360°∘- 60°)
tanx = tan150°∘ or tanx = tan330°∘
tanx = tan5π/6 or tanx = tan11π/6
Here, the principal solutions are 5π/6, 11 π/6
∴ tan x = tan 5π/6
⇒x = nπ + 5π/3 where, n ∈ Z
Question 4. cosec x = – 2
Solution:
Given: cosec x = – 2
It can be written as, sin x = -1/2
Here x lies in third or fourth quadrant.
∴ sinx = -sin30°∘= sin(180° + 30°) or sinx = sin(360°∘- 30°)
sinx = sin210°∘ or sinx = sin330°∘
sinx = sin7π/6 or sinx = sin11π/6
Here, the principal solutions are 7π/6, 11 π/6
∴ sin x = -sin π/6
⇒ x = nπ + (−1)n7π/6 where, n ∈ Z
Find the general solution for each of the following equations:
Question 5. cos 4x = cos 2x
Solution:
Given: cos 4x = cos 2x
4x = 2nπ ± 2x, n ∈ Z
4x – 2x = 2nπ or 4x + 2x = 2nπ, n ∈ Z
2x = 2nπ or 6x = 2nπ, n ∈ Z
2x = 2nπ or 6x = 2nπ, n ∈ Z
x = nπ or x = 3nπ, n ∈ Z
Therefore, the principal solutions are nπ, nπ/3
Question 6. cos 3x + cos x – cos 2x = 0
Solution:
Given: cos 3x + cos x – cos 2x = 0
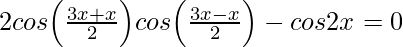
2cos2xcosx – cos2x = 0
cos2x(2cosx – 1) = 0
cos2x = 0 or 2cosx – 1 = 0
2x = (2n + 1)π/2 or cosx = 1/2 = cosπ/3, n ∈ z
x = (2n + 1)π/4 or x = 2nπ ± 2π/3, n ∈ z
Question 7. sin 2x + cos x = 0
Solution:
Given: sin 2x + cos x = 0
2sinxcosx + cosx = 0
cosx(2sinx + 1) = 0
cosx = 0 or 2sinx + 1 = 0
x = (2n + 1)π/2 or sinx = −1/2 = −sinπ/6, n ∈ z
x = (2n + 1)π/4 or x = 2nπ ± 2π/3, n ∈ z
x = (2n + 1)π/4 or x = nπ + (-1)n-π/6, n ∈ Z
x = (2n + 1)π/4 or x = nπ + (-1)n7π/6, n ∈ Z
Question 8. sec22x = 1 – tan 2x
Solution:
Given: sec22x = 1 – tan 2x
1 + tan22x = 1 – tan2x
tan2x(tan2x + 1) = 0
tan2x = 0 or tan2x + 1 = 0
2x = nπ or tan2x – 1 = –tanπ/4
x = nπ/2 or x = nπ/2 + 3π/8, n = Z
Question 9. sin x + sin 3x + sin 5x = 0
Solution:
Given: sin x + sin 3x + sin 5x = 0
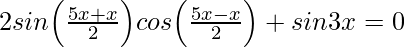
2sin3xcos2x + sin3x = 0
sin3x(2cos2x + 1) = 0
sin3x = 0 or 2cos2x + 1 = 1
3x = nπ or cos2x = -1/2 = cos2π/3, n ∈ z
x = nπ/3 or 2x = nπ/2 ± 2π/3, n ∈ z
x = nπ/3 or x = nπ ± π/3, n ∈ z
Share your thoughts in the comments
Please Login to comment...