Question 1. Find the 20th and nth terms of the G.P 5/2, 5/4, 5/8, …
Solution:
According to the question
G.P: 5/2, 5/4, 5/8, …
So, first term(a) = 5/2
So, the common ratio(r) = 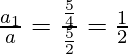
Find: 20th and nth terms of the given G.P
So, the nth term of G.P can be expressed using formula:
an = arn – 1
Where a is 1st term and r is the common ratio.
Now we find the 20th terms of the given G.P:
a20 = (5/2)(1/2)20-1 = (5/2)(1/2)19= 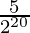
Find the nth terms of the given G.P:
an = 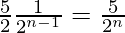
Question 2. Find the 12th term of a G.P. whose 8th term is 192 and the common ratio is 2.
Solution:
According to the question
Common ration(r) = 2
and 8th term is 192
So let us considered a be the first term
So,
a8 = ar7
ar7 = 192
a(2)7 = 192
a = 3/2
Find: 12th term of a G.P.
As we know that the nth term of G.P can be expressed using formula:
an = arn – 1
Where a is 1st term and r is the common ratio
So, we find 12th term of a G.P.
a12 = ar12 – 1
a12 = ar11
a12 = (3/2)(2)11
a12 = 3072
Question 3. The 5th, 8th and 11th terms of a G.P. are p, q and s, respectively. Show that q2 = ps.
Solution:
According to the question
The 5th, 8th and 11th terms of a G.P. are p, q and s
Prove: q2 = ps
Proof:
Let a G.P. with first term a and common ratio r,
So, a5 = ar4 = p ….(1)
a8 = ar7= q ….(2)
a11 = ar10 = s ….(3)
Now divide eq(2) by (1), we get
ar7/ar4 = q/p
r3 = q/p ….(4)
Now divide eq(3) by (2), we get
ar10/ar7= s/q
r3 = s/q ….(5)
From eq(4) and (5), we get
q/p = s/q
q2 = ps
Hence Proved
Question 4. The 4th term of a G.P. is square of its second term, and the first term is – 3. Determine its 7th term.
Solution:
According to the question
First term(a) = – 3
and the 4th term of a G.P. is square of its second term
Find: 7th term
Let us considered r be the common ratio
As we know that the nth term of G.P can be expressed using formula:
an = arn – 1
Where a is 1st term and r is the common ratio
So, a4 = ar3
It is given that the 4th term of a G.P. is square of its second term
a4 = (a2)2
ar3 = (a2)2
ar3 = (ar)2
ar3 = a2r2
r = a
Now put the value of a, we get
r = -3
Now, we find the 7th term
a7 = ar7 – 1
a7 = ar6
= −3 x (−3)6 =−2187
Question 5. Which term of the following sequences:
(a) 2, 2√2, 4, … is 128 ?
Solution:
According to the question
G.P.: 2, 2√2, 4, …
So, first term(a) = 2
So, the common ratio(r) = √2
As we know that, the nth term of G.P can be expressed using formula:
an = arn – 1
Where a is 1st term and r is the common ratio.
128 = 2(√2)n – 1
(2)7 = 2(√2)n – 1
(2)7 = 2((2)1/2)n – 1
(2)7 = 2(2)(n – 1)/2
(2)6 = (2)(n – 1)/2
6 = (n – 1)/2
12 = n – 1
12 + 1 = n
n = 13
Hence, the 13th term of the G.P. is 128
(b) √3, 3, 3√3, …. is 729 ?
Solution:
According to the question
G.P.: √3, 3, 3√3, ….
So, first term(a) = √3
So, the common ratio(r) = √3
As we know that, the nth term of G.P can be expressed using formula:
an = arn – 1
Where a is 1st term and r is the common ratio.
729 = √3(√3)n-1
(3)6 = √3(√3)n-1
(3)6 = (3)1/2((3)1/2)n-1
(3)6 = (3)1/2(3)n-1/2
(3)6 = (3)1/2+(n-1)/2
6 = 1/2 + (n – 1)/2
6 – 1/2 = (n – 1)/2
(12 – 1)/2 = (n – 1)/2
11 = n – 1
n = 12
Hence, the 12th term of the G.P. is 729
(c)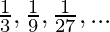 is
is 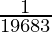 ?
?
Solution:
According to the question
G.P.: 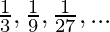
So, first term(a) = 1/3
So, the common ratio(r) = 1/3
As we know that, the nth term of G.P can be expressed using formula:
an = arn – 1
Where a is 1st term and r is the common ratio.
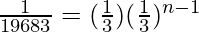
(1/3)9 = (1/3)n
n = 9
Hence, the 9th term of the G.P. is 1/19683
Question 6. For what values of x, the numbers -2/7, x. -7/2… are in G.P.?
Solution:
According to the question
Numbers are -2/7, x. -7/2…
The common ration is (r) = 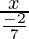 = -7x/2
= -7x/2
Again the common ration(r) = = 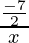 = -7/2x
= -7/2x
So,
-7x/2 = -7/2x
7x/2 = 2/7x
14x2 = 14
x2 = 14/14
x = ±1
Find the sum to indicated number of terms in each of the geometric progressions in Exercises 7 to 10:
Question 7. 0.15, 0.015, 0.0015, … 20 terms.
Solution:
According to the question
G.P.: 0.15, 0.015, 0.0015, …
So, first term(a) = 0.15
So, the common ratio(r) = 0.1
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
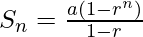
So, S20 = (0.15)[(1 – (0.1)20)/(1 – 0.1)]
= (0.15/0.9)(1 – (0.1)20)
= 1/6(1 – (0.1)20)
Question 8. √7, √21, 3√7,… n terms.
Solution:
According to the question
G.P.: √7, √21, 3√7,…
So, first term(a) = √7
So, the common ratio(r) = √3
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
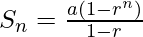
So, Sn = (√7)[(1 – (√3)n)/(1 – √3)]
= (√7)[(1 – (√3)n)/(1 – √3)] x [(1 + √3)/(1 + √3)]
= -(√7)(1 + √3)/2(1 – (3)n/2)
= (√7)(1 + √3)/2((3)n/2 – 1)
Question 9. 1, -a, a2, -a3,… n terms (if a ≠ – 1).
Solution:
According to the question
G.P.: 1, -a, a2, -a3,…
So, first term(a) = 1
So, the common ratio(r) = -a
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
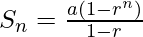
So, 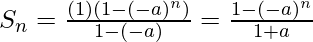
Question 10. x3, x5, x7, … n terms (if x ≠ ± 1).
Solution:
According to the question
G.P.: x3, x5, x7, …
So, first term(a) = x3
So, the common ratio(r) = x2
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
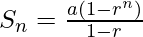
So,
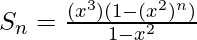
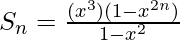
Question 11. Evaluate 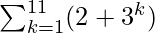
Solution:
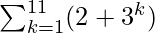 = (2 + 31) + (2 + 32) + (2 + 33) + …. + (2 + 311)
= (2 + 31) + (2 + 32) + (2 + 33) + …. + (2 + 311)
= (2 + 2 + …11 terms) + (3 + 32 + 33+…11 terms)
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
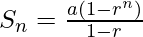
So, Sn = 2 x 11 + 3(311 – 1)/3 – 1
Sn = 22 + 3/2((311 – 1))
Question 12. The sum of first three terms of a G.P. is 39/10 and their product is 1. Find the common ratio and the terms.
Solution:
Let us considered the three terms a/r, a, ar of the G.P.
According to the question
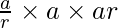 = 1
= 1
a3 = 1
a = 1
Also.
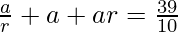
Now put the value of a, we get
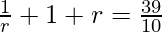
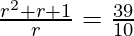
10r2 + 10r + 10 = 39r
10r2 – 29r + 10 = 0
On solving the equation, we get
r = 2/5, 5/2
So, the G.P. is 5/2, 1, 2/5.
Question 13. How many terms of G.P. 3, 32, 33, … are needed to give the sum 120?
Solution:
According to the question
G.P.: 3, 32, 33, …
So, first term(a) = 3
So, the common ratio(r) = 3
Sn = 120
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
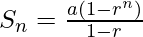
Sn = (3)(1 – (3)n)(1-3)
120 = (3)(1 – (3)n)
-240 = (3)(1 – (3)n)
-80 = 1 – (3)n
-80 – 1 = – (3)n
-81 = – (3)n
(3)4 = (3)n
n = 4
Hence, 4 terms of G.P. are needed to give the sum 120
Question 14. The sum of first three terms of a G.P. is 16 and the sum of the next three terms is 128. Determine the first term, the common ratio, and the sum to n terms of the G.P.
Solution:
Let us considered the first three terms of the G.P. are a, ar, ar2 and
first term of G.P. be a and common ratio r.
Find: the first term, the common ratio, and the sum to n terms of the G.P.
According to the question
a + ar + ar2 = 16
a(1 + r + r2) = 16 …….(1)
ar3 + ar4 + ar5 = 128
ar3(1 + r + r2) = 128 …….(2)
Now divide eq(2) by (1), we get
ar3(1 + r + r2)/ a(1 + r + r2) = 128/16
r3 = 8
r = 2
Now put the value of r in eq(1), we get
a(1 + (2) + (2)2) = 16
a(1 + 2 + 4) = 16
a(7) = 16
a = 16/7
Now we find the sum to n terms of the G.P.
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
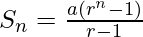
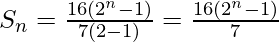
Question 15. Given a G.P. with a = 729 and 7th term 64, determine S7.
Solution:
According to the question
The first term(a) = 729
and 7th term 64
Find: S7
Let the common ratio be r.
a7 = ar6 = 64
r6 = 64/729
r = ±2/3
Now we find the sum to 7th terms of the G.P.
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
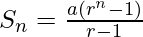
On taking r = +2/3
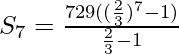 = 2059
= 2059
On taking r = -2/3
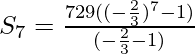 = 463
= 463
Question 16. Find a G.P. for which sum of the first two terms is – 4 and the fifth term is 4 times the third term.
Solution:
Let the first term of the G.P. be a and common ratio be r.
According to the question
a + ar = -4
a5 = 4(a3)
So, ar4 = 4(ar2)
r2 = 4
r = ±2
When r = +2 then
a + ar = a + 2a = 3a = −4
a = -4/3
Then the G.P. is 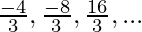
When r = -2 then
a + ar = a − 2a = −a = −4
a = 4
Then the G.P. is 4, -8, 16, -32,…
Share your thoughts in the comments
Please Login to comment...