Evaluates the following limits:
Question 18. Limx→1{√(5x – 4) – √x}/(x3 – 1)
Solution:
We have, Limx→1{√(5x – 4) – √x}/(x3 – 1)
Find the limit of the given equation
When we put x = 1, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 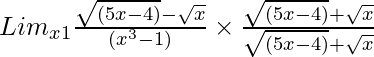
= Limx→1{(5x – 4) – x}/[{√(5x – 4) + √x}(x3 – 1)]
= Limx→1{4(x – 1)}/[{√(5x – 4) + √x}(x-1)(x2 + x + 1)]
= Limx→1(4)/[{√(5x – 4) + √x}(x2 + x + 1)]
Now put x = 1, we get
= 4/{(3)(√1 + √1)}
= 4/6
= 2/3
Question 19. Limx→2{√(1 + 4x) – √(5 + 2x)}/(x – 2)
Solution:
We have, Limx→2{√(1 + 4x) – √(5 + 2x)}/(x – 2)
Find the limit of the given equation
When we put x = 2, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 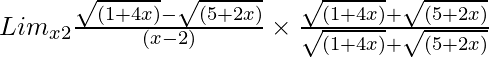
= Limx→2{√(1 + 4x) – √(5+2x)}/[(x – 2){√(1 + 4x) + √(5 + 2x)}]
= Limx→2{(1 + 4x) – (5 + 2x)}/[(x – 2){√(1 + 4x) + √(5 + 2x)}]
= Limx→2{2(x – 2)}/[(x – 2){√(1 + 4x) + √(5 + 2x)}]
= Limx→2(2)/{√(1 + 4x) + √(5 + 2x)}
Now put x = 2, we get
= 2/{√(1 + 8) + √(5 + 4)}
= 2/(3 + 3)
= 1/3
Question 20. Limx→1{√(3 + x) – √(5 – x)}/(x2 – 1)
Solution:
We have, Limx→1{√(3 + x) – √(5 – x)}/(x2 – 1)
Find the limit of the given equation
When we put x = 1, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 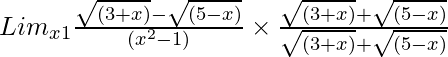
= Limx→1{(3 + x) – (5 – x)}/[(x2 – 1){√(3 + x) + √(5 – x)}]
= Limx→1{2(x – 1)}/[(x – 1)(x + 1){√(3 + x) + √(5 – x)}]
= Limx→1(2)/[(x + 1){√(3 + x) + √(5 – x)}]
Now put x = 1, we get
= 2/{2(2 + 2)}
= 1/4
Question 21. Limx→0{√(1 + x2) – √(1 – x2)}/(x)
Solution:
We have, Limx→0{√(1 + x2) – √(1 – x2)}/(x)
Find the limit of the given equation
When we put x = 0, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 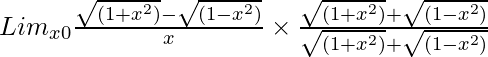
= Limx→0{(1 + x2) – (1 – x2)}/[x{√(1 + x2) + √(1 – x2)}]
= Limx→0{(1 + x2) – (1 – x2)}/[x{√(1 + x2) + √(1 – x2)}]
= Limx→0(2x2/[x{√(1 + x2) + √(1 – x2)}]
= Limx→0(2x/{√(1 + x2) + √(1 – x2)}
Now put x = 0, we get
= 2 × 0/(√1 + √1)
= 0
Question 22. Limx→0{√(1 + x + x2) – √(x + 1)}/(2x2)
Solution:
We have, Limx→0{√(1 + x + x2) – √(x + 1)}/(2x2)
Find the limit of the given equation
When we put x = 0, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 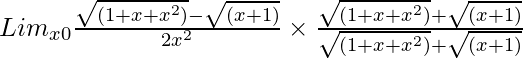
= Limx→0{(1 + x + x2) – (x + 1)}/[2x2{√(1 + x + x2) – √(x + 1)}]
= Limx→0(x2)/[2x2{√(1 + x + x2) – √(x + 1)}]
= Limx→0(1)/[2{√(1 + x + x2) – √(x + 1)}]
Now put x = 0, we get
= 1/{2(√1 + √1)
= 1/4
Question 23. Limx→4{2 – √x}/(4 – x)
Solution:
We have, Limx→4{2 – √x}/(4 – x)
Find the limit of the given equation
When we put x = 4, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 
= Limx→4{4 – x}/[(4 – x){2 + √x}]
= Limx→4{4 – x}/[(4 – x){2 + √x}]
= Limx→4(1)/{2 + √x}
Now put x = 4, we get
= 1/(2 + 2)
= 1/4
Question 24. Limx→a(x – a)/{√x – √a}
Solution:
We have, Limx→a(x – a)/{√x – √a}
Find the limit of the given equation
When we put x = a, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 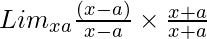
= Limx→a[(x – a){√x – √a}]/(x – a)
= Limx→a{√x + √a}
Now put x = a, we get
= √a + √a
= 2√a
Question 25. Limx→0{√(1 + 3x) – √(1 – 3x)}/(x)
Solution:
We have, Limx→0{√(1 + 3x) – √(1 – 3x)}/(x)
Find the limit of the given equation
When we put x = a, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 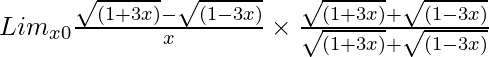
= Limx→0{(1 + 3x) – (1 – 3x)}/[(x){√(1 + 3x) – √(1 – 3x)}]
= Limx→0(6x)/[(x){√(1 + 3x) – √(1 – 3x)}]
= Limx→0(6)/{√(1 + 3x) – √(1 – 3x)}
Now put x = 0, we get
= 6/(√1 + √1)
= 6/2
= 3
Question 26. Limx→0{√(2 – x) – √(2 + x)}/(x)
Solution:
We have, Limx→0{√(2 – x) – √(2 + x)}/(x)
Find the limit of the given equation
When we put x = 0, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 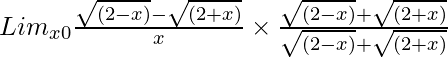
= Limx→0{(2 – x) – (2 + x)}/[x{√(2 – x) + √(2 + x)}]
= Limx→0(-2x)/[x{√(2 – x) + √(2 + x)}]
= Limx→0(-2)/{√(2 – x) + √(2 + x)}
Now put x = 0, we get
= (-2)/(√2 + √2)
= (-2)/(2√2)
= -1/(√2)
Question 27. Limx→1{√(3 + x) – √(5 – x)}/(x2 – 1)
Solution:
We have, Limx→1{√(3 + x) – √(5 – x)}/(x2 – 1)
Find the limit of the given equation
When we put x = 1, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 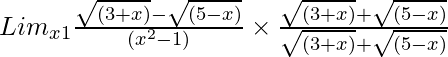
= Limx→1{(3 + x) – (5 – x)}/[(x2 – 1){√(3 + x) + √(5 – x)}]
= Limx→1{2(x – 1)}/[(x – 1)(x + 1){√(3 + x) + √(5 – x)}]
= Limx→1(2)/[(x + 1){√(3 + x) + √(5 – x)}]
Now put x = 1, we get
= 2/{(2)(√4 + √4)}
= 2/8
= 1/4
Question 28. Limx→1{(2x – 3)(√x – 1)}/(3x2 + 3x – 6)
Solution:
We have, Limx→1{(2x – 3)(√x – 1)}/(3x2 + 3x – 6)
Find the limit of the given equation
When we put x = 1, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= Limx→1{(2x – 3)(x – 1)}/[(3x2 + 3x – 6)(√x + 1)]
= Limx→1{(2x – 3)(x – 1)}/[3(x2 + x – 2)(√x + 1)]
= Limx→1{(2x – 3)(x – 1)}/[3(x – 1)(x + 2)(√x + 1)]
= Limx→1(2x – 3)/[3(x + 2)(√x + 1)]
Now put x = 1, we get
= (2 – 3)/{3(3)(√1 + 1)
= -1/(3 × 3 × 2)
= -1/18
Question 29. Limx→0{√(1 + x2) – √(1 + x)}/{√(1 + x3) – √(1 + x)}
Solution:
We have, Limx→0{√(1 + x2) – √(1 + x)}/{√(1 + x3) – √(1 + x)}
Find the limit of the given equation
When we put x = 0, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
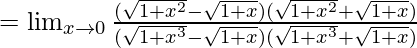
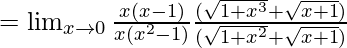
![Rendered by QuickLaTeX.com =\lim_{x\to0}\frac{[(1+x^2)-(1+x)]}{[(1+x^3)-(1+x)}×\frac{(\sqrt{1+x^3}+\sqrt{x+1})}{(\sqrt{1+x^2}+\sqrt{x+1})}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8a5153c28b82f5f1356d9c8282be84a8_l3.png)
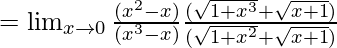
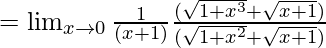
Now put x = 0, we get
= (√1 + √1)/{1(√1 + √1)}
= 2/2
= 1
Question 30. Limx→1{x2 – √x}/{√x – 1}
Solution:
We have, Limx→1{x2 – √x}/{√x – 1}
Find the limit of the given equation
When we put x = 1, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= Limx→1{√x(x√x -1)}/{√x – 1}
= Limx→1{√x(x3/2 – 1)}/{√x – 1}
= Limx→1[√x{(√x)3 – 1}]/{√x – 1}
= Limx→1[(√x)(√x – 1)(x + √x + 1)]/{√x – 1}
= Limx→1[(√x)(x + √x + 1)]
Now put x = 1, we get
= (√1)(1 + √1 + 1)
= 3
Question 31. Limh→0{√(x + h) – √x}/(h), x ≠ 0
Solution:
We have, Limh→0{√(x + h) – √x}/(h)
Find the limit of the given equation
When we put h = 0, this expression takes the form of 0/0.
So, on rationalizing the given equation we get
= 
= Limh→0{(x + h) – x}/[h{√(x + h) + √x}]
= Limh→0(h)/[h{√(x + h) + √x}]
= Limh→0(1)/{√(x + h) + √x}
Now put x = 0, we get
= 1/(√x + √x)
= 1/(2√x)
Question 32. Limx→√10{√(7 + 2x) – (√5 + √2)}/(x2 – 10)
Solution:
We have, Limx→√10{√(7 + 2x) – (√5 + √2)}/(x2 – 10)
= Limx→√10{√(7 + 2x) – √(√5 + √2)2}/{(x – √10)(x + √10)}
= Limx→√10{√(7 + 2x) – √(5 + 2 + 2√5√2)}/{(x – √10)(x + √10)}
= Limx→√10{√(7 + 2x) – √(7 + 2√10)}/{(x – √10)(x + √10)}
On rationalizing numerator.
=
=
=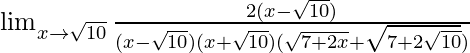
Now put x = √10, we get
=
=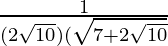
=
= 1/{(2√10)(√5 + √2)}
On rationalizing denominator.
= (√5 – √2)/{(2√10)(5 – 2)}
= (√5 – √2)/(6√10)
Question 33. Limx→√6{√(5 + 2x) – (√3 + √2)}/(x2 – 6)
Solution:
We have, Limx→√6{√(5 + 2x) – (√3 + √2)}/(x2 – 6)
= Limx→√6{√(5 + 2x) – √(√3 + √2)2}/{(x – √6)(x + √6)}
= Limx→√6{√(5 + 2x) – √(3 + 2 + 2√3√2)}/{(x – √6)(x + √6)}
= Limx→√6{√(5 + 2x) – √(5 + 2√6)}/{(x -√6)(x + √6)}
On rationalizing numerator.
= 
=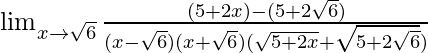
=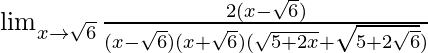
=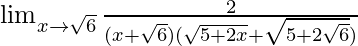
Now put x = √6, we get
=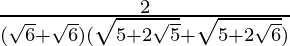
=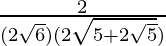
=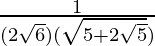
= 1/{(2√6)(√3 + √2)}
On rationalizing denominator, we get
= (√3 – √2)/{(2√6)(3 – 2)}
= (√3 – √2)/(2√6)
Question 34. Limx→√2{√(3 + 2x) – (√2 + 1)}/(x2 – 2)
Solution:
We have, Limx→√2{√(3 + 2x) – (√2 + 1)}/(x2 – 2)
= Limx→√2{√(3 + 2x) – √(√2 + 1)2}/{(x – √2)(x + √2)}
= Limx→√2{√(3 + 2x) – √(2 + 1 + 2√3)}/{(x – √2)(x + √2)}
= Limx→√2{√(3 + 2x) – √(3 + 2√3)}/{(x – √2)(x + √2)}
On rationalizing numerator.
=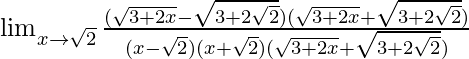
=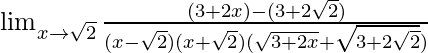
=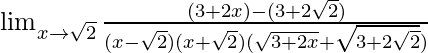
=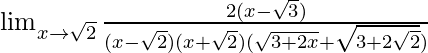
=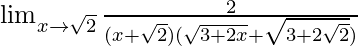
Now put x = √2, we get
=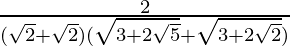
=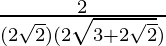
=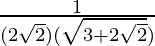
= 1/{(2√2)(√2 + 1)}
On rationalizing denominator, we get
= (√2 – 1)/{(2√2)(2 – 1)}
= (√2 – 1)/(2√2)
Share your thoughts in the comments
Please Login to comment...