Prove the following by using the principle of mathematical induction for all n ∈ N:
Question 1: 1 + 3 + 32 + …….. + 3n-1 = 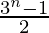
Solution:
We have,
P(n) = 1 + 3 + 32 + …….. + 3n-1 = 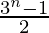
For n=1, we get
P(1) = 1 = 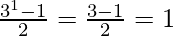
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1 + 3 + 32 + …….. + 3k-1 = 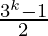 ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1 + 3 + 32 + …….. + 3k-1 + 3(k+1)-1
= (1 + 3 + 32 + …….. + 3k-1) + 3k
From Eq(1), we get
= 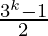 + 3k
+ 3k
= 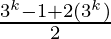
= 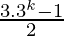
= 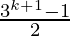
Hence,
P(k+1) = 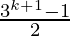
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 2: 1 + 23 + 33 + ……….. + n3 = ![Rendered by QuickLaTeX.com [\frac{n(n+1)}{2} ]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-503895ebcf6131d03275e7171f4e28c8_l3.png)
Solution:
We have,
P(n) = 1 + 23 + 33 + ……….. + n3 = ![Rendered by QuickLaTeX.com [\frac{n(n+1)}{2} ]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-503895ebcf6131d03275e7171f4e28c8_l3.png)
For n=1, we get
P(1) = 1 = ![Rendered by QuickLaTeX.com [\frac{1(1+1)}{2} ]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e64f700103072806aa25fabd3617b720_l3.png) = 1
= 1
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1 + 23 + 33 + ……….. + k3 = ![Rendered by QuickLaTeX.com [\frac{k(k+1)}{2} ]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-49f3c3e7b75fc804a23c79f95773c5d2_l3.png) ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1 + 23 + 33 + ……….. + k3 + (k+1)3
= (1 + 23 + 33 + ……….. + k3) + (k+1)3
From Eq(1), we get
= ![Rendered by QuickLaTeX.com [\frac{k(k+1)}{2} ]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-49f3c3e7b75fc804a23c79f95773c5d2_l3.png) + (k+1)3
+ (k+1)3
= 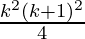 + (k+1)3
+ (k+1)3
= 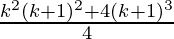
Taking (k+1)2, we get
= 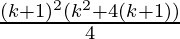
= 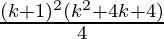
= 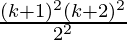
= ![Rendered by QuickLaTeX.com [\frac{(k+1)((k+1)+1)}{2} ]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d301d9d5b1beb11d634d3d0438bac538_l3.png)
Hence,
P(k+1) = ![Rendered by QuickLaTeX.com [\frac{(k+1)((k+1)+1)}{2} ]^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d301d9d5b1beb11d634d3d0438bac538_l3.png)
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 3: 1 + 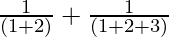 + ……. +
+ ……. + 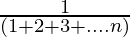 =
= 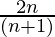
Solution:
We have,
P(n) = 1 + 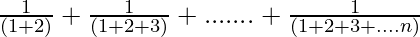 =
= 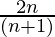
For n=1, we get
P(1) = 1 = 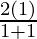 = 1
= 1
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1 + 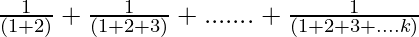 =
= 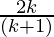 ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1 + 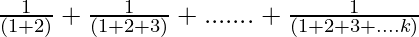 +
+ 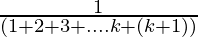
= (1 + 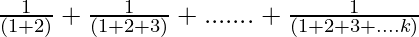 ) +
) + 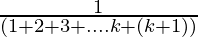
From Eq(1), we get
= 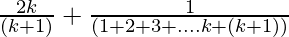
As we know that,
Sum of first natural number,
1 + 2 + 3 + …… + n = 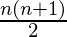
So, we get
= 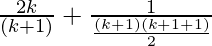
= 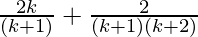
= 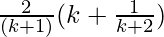
= 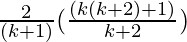
= 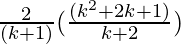
= 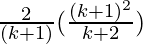
= 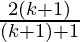
Hence,
P(k+1) = 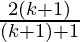
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 4: 1.2.3 + 2.3.4 +…+ n(n+1) (n+2) = 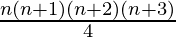
Solution:
We have,
P(n) = 1.2.3 + 2.3.4 +…+ n(n+1) (n+2) = 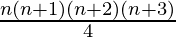
For n=1, we get
P(1) = 1.2.3 = 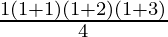 =
= 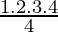 = 1.2.3
= 1.2.3
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1.2.3 + 2.3.4 +…+ k(k+1) (k+2) = 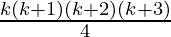 ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1.2.3 + 2.3.4 +…+ k(k+1) (k+2) + (k+1)(k+1+1) (k+1+2)
= (1.2.3 + 2.3.4 +…+ k(k+1) (k+2)) + (k+1)(k+2) (k+3)
From Eq(1), we get
= 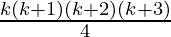 + (k+1)(k+2)(k+3)
+ (k+1)(k+2)(k+3)
= (k+1)(k+2) (k+3) (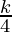 + 1)
+ 1)
= 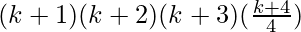
= 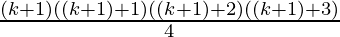
Hence,
P(k+1) = 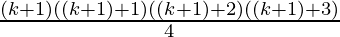
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 5: 1.3 + 2.32 + 3.33 +…+ n.3n = 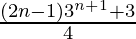
Solution:
We have,
P(n) = 1.3 + 2.32 + 3.33 +…+ n.3n = 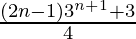
For n=1, we get
P(1) = 1.3 = 3 = 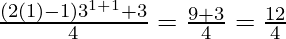 = 3
= 3
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1.3 + 2.32 + 3.33 +…+ k.3k = 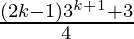 ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1.3 + 2.32 + 3.33 +…+ k.3k + (k+1).3(k+1)
= (1.3 + 2.32 + 3.33 +…+ k.3k) + (k+1).3(k+1)
From Eq(1), we get
= 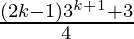 + (k+1).3(k+1)
+ (k+1).3(k+1)
= 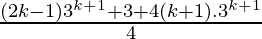
= 3k+1 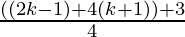
= 3k+1 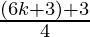
= 3k+1 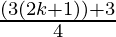
= 3(k+1)+1 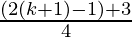
Hence,
P(k+1) = 3(k+1)+1 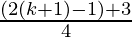
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 6: 1.2 + 2.3 + 3.4 +…+ n.(n+1) = ![Rendered by QuickLaTeX.com [\frac{n(n+1)(n+2)}{3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-69de8a069d88755a83c28347803392ca_l3.png)
Solution:
We have,
P(n) = 1.2 + 2.3 + 3.4 +…+ n.(n+1) = ![Rendered by QuickLaTeX.com [\frac{n(n+1)(n+2)}{3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-69de8a069d88755a83c28347803392ca_l3.png)
For n=1, we get
P(1) = 1.2 = 2 = ![Rendered by QuickLaTeX.com [\frac{1(1+1)(1+2)}{3}] = [\frac{1(2)(3)}{3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8d0c2eb0bca51e6cce91d6e770d1cb21_l3.png) = 2
= 2
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1.2 + 2.3 + 3.4 +…+ k.(k+1) = ![Rendered by QuickLaTeX.com [\frac{k(k+1)(k+2)}{3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ce17fa7f7fe307887dd6c82ee43c00ad_l3.png) ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1.2 + 2.3 + 3.4 +…+ k.(k+1) + (k+1)(k+1+1)
= (1.2 + 2.3 + 3.4 +…+ k.(k+1)) + (k+1)(k+2)
From Eq(1), we get
= ![Rendered by QuickLaTeX.com [\frac{k(k+1)(k+2)}{3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ce17fa7f7fe307887dd6c82ee43c00ad_l3.png) + (k+1)(k+2)
+ (k+1)(k+2)
= ![Rendered by QuickLaTeX.com [\frac{k(k+1)(k+2)+3(k+1)(k+2)}{3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-deadf50db11de1d37d735af13c026213_l3.png)
= (k+1)(k+2) ![Rendered by QuickLaTeX.com [\frac{k+3}{3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-46e712b7026c6908f7fd9de07d5328fb_l3.png)
= ![Rendered by QuickLaTeX.com [\frac{(k+1)(k+2)(k+3)}{3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-67733a1524a015d89a4e7806baa2c4c1_l3.png)
= ![Rendered by QuickLaTeX.com [\frac{(k+1)((k+1)+1)((k+1)+2)}{3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6fdba53f3a08e612c699ad2509897107_l3.png)
Hence,
P(k+1) = ![Rendered by QuickLaTeX.com [\frac{(k+1)((k+1)+1)((k+1)+2)}{3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6fdba53f3a08e612c699ad2509897107_l3.png)
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 7: 1.3 + 3.5 + 5.7 +…+ (2n–1) (2n+1) =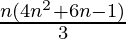
Solution:
We have,
P(n) = 1.3 + 3.5 + 5.7 +…+ (2n–1) (2n+1) = 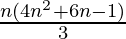
For n=1, we get
P(1) = 1.3 = 3 = 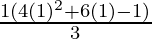 =
= 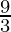 = 3
= 3
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1.3 + 3.5 + 5.7 +…+ (2k–1) (2k+1) = 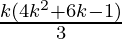 ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1.3 + 3.5 + 5.7 +…+ (2k–1) (2k+1) + (2(k+1)-1)(2(k+1)+1)
= (1.3 + 3.5 + 5.7 +…+ (2k–1) (2k+1)) + (2k+1)(2k+3)
From Eq(1), we get
= 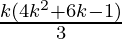 + (4k2+8k+3)
+ (4k2+8k+3)
= 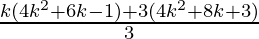
= 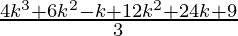
= 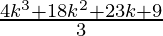
=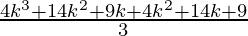
= 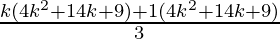
= 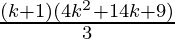
= 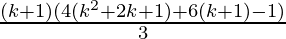
= 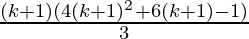
Hence,
P(k+1) = 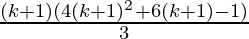
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 8: 1.2 + 2.22 + 3.23 + …+n.2n = (n–1) 2n + 1 + 2
Solution:
We have,
P(n) = 1.2 + 2.22 + 3.23 + …+n.2n = (n–1) 2n + 1 + 2
For n=1, we get
P(1) = 1.2 = 2 = (1–1) 2(1) + 1 + 2 = 2
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 1.2 + 2.22 + 3.23 + …+k.2k = (k–1) 2k + 1 + 2 ……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 1.2 + 2.22 + 3.23 + …+k.2k + (k+1).2(k+1)
= (1.2 + 2.22 + 3.23 + …+k.2k) + (k+1).2(k+1)
From Eq(1), we get
= (k–1) 2k + 1 + 2 + (k+1).2k+1
= 2k + 1((k–1) + (k+1)) + 2
= 2k + 1(2k) + 2
= k.2k+1+1 + 2
= ((k+1)-1).2(k+1)+1 + 2
Hence,
P(k+1) = ((k+1)-1).2(k+1)+1 + 2
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 9: 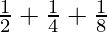 + …… +
+ …… + 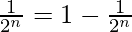
Solution:
We have,
P(n) = 
For n=1, we get
P(1) = 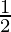 = 1 –
= 1 – 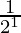 =
= 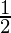
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 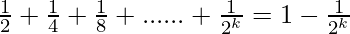 ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 
= (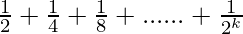 ) +
) + 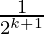
From Eq(1), we get
= 1 – 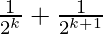
= 1 – 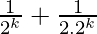
= 1 – 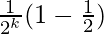
= 1 – 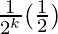
= 1 –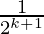
Hence,
P(k+1) = 1 – 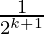
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 10: 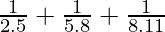 + …… +
+ …… + 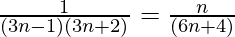
Solution:
We have,
P(n) = 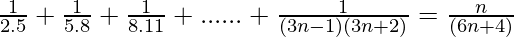
For n=1, we get
P(1) = 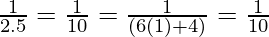
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 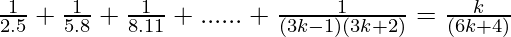 ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 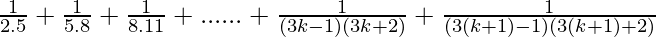
= (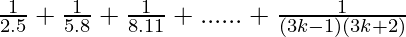 ) +
) + 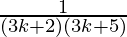
From Eq(1), we get
= 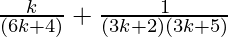
= 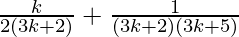
= 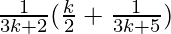
= 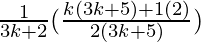
= 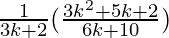
= 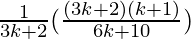
= 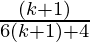
Hence,
P(k+1) = 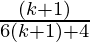
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 11: 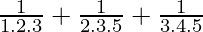 + …… +
+ …… + 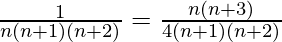
Solution:
We have,
P(n) = 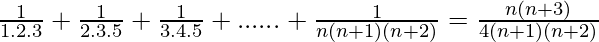
For n=1, we get
P(1) = 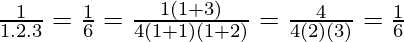
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 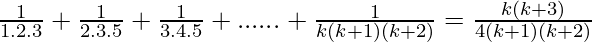 ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 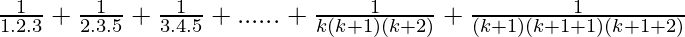
= (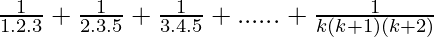 ) +
) + 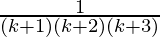
From Eq(1), we get
= 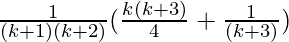
= 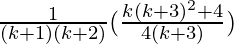
= 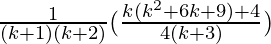
= 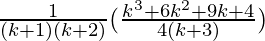
= 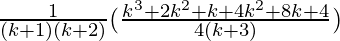
= 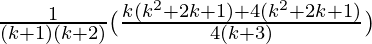
= 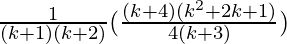
= 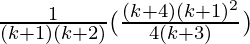
= 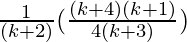
= 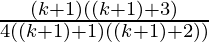
Hence,
P(k+1) = 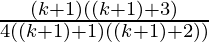
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 12: a + ar + ar2 + …… + arn-1 = 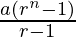
Solution:
We have,
P(n) = a + ar + ar2 + …… + arn-1 = 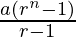
For n=1, we get
P(1) = a = 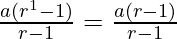 = a
= a
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = a + ar + ar2 + …… + ark-1 =  ……………..(1)
……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = a + ar + ar2 + …… + ark-1 + ar(k+1)-1
= (a + ar + ar2 + …… + ark-1) + ark
From Eq(1), we get
=  + ark
+ ark
= 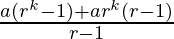
= 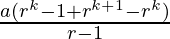
= 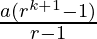
Hence,
P(k+1) = 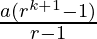
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Question 13: (1+ 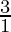 ) (1+
) (1+ 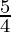 ) (1+
) (1+ 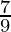 ) ….. (1+
) ….. (1+ 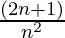 ) = (n+1)2
) = (n+1)2
Solution:
We have,
P(n) = 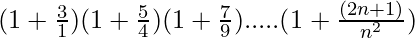 = (n+1)2
= (n+1)2
For n=1, we get
P(1) = 1+ 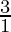 = 1+3 = 4 = (1+1)2 = 22 = 4
= 1+3 = 4 = (1+1)2 = 22 = 4
So, P(1) is true
Assume that P(k) is true for some positive integer n=k
P(k) = 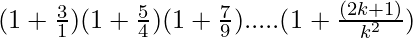 = (k+1)2 ……………..(1)
= (k+1)2 ……………..(1)
Let’s prove that P(k + 1) is also true. Now, we have
P(k+1) = 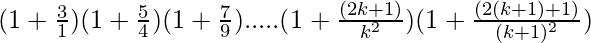
= 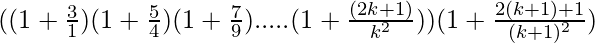
From Eq(1), we get
= (k+1)2 (1+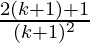 )
)
= (k+1)2 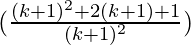
= (k+1)2 + 2(k+1) + 1
= {(k+1)}2
Hence,
P(k+1) = {(k+1)}2
Thus, P(k + 1) is true, whenever P (k) is true.
Hence, from the principle of mathematical induction, the statement P(n) is true for all natural numbers n.
Share your thoughts in the comments
Please Login to comment...