Class 11 NCERT Solutions- Chapter 5 Complex Numbers And Quadratic Equations – Miscellaneous Exercise on Chapter 5 | Set 1
Last Updated :
01 Apr, 2021
Question 1. Evaluate ![Rendered by QuickLaTeX.com \left[i^{18}+\left(\frac{1}{i}\right)^{25}\right]^3](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9204b8902fbce319746190720a4ed916_l3.png)
Solution:
![Rendered by QuickLaTeX.com \displaystyle\left[i^{18}+\left(\frac{1}{i}\right)^{25}\right]^3\\ =\left[i^{4\times4+2}+\frac{1}{i^{4\times6+1}}\right]^3\\ =\left[(i^4)^{4}.i^2+\frac{1}{(i^4)^6.i}\right]^3\\ =\left[i^2+\frac{1}{i}\right]^3\ \ \ \ \ \ [i^4=1]\\ =\left[-1+\frac{1}{i}\times\frac{i}{i}\right]^3\ \ \ \ \ \ [i^2=-1]\\ =\left[-1+\frac{i}{i^2}\right]^3](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-de17eb3266c9f824364c873e58d1b97b_l3.png)
= [-1 – i]3
= (-1)3 [1 + i]3
= -[13 + i3 + 3 × 1 × i (1 + i)]
= -[1 + i3 + 3i + 3i2]
= -[1 – i + 3i – 3]
= -[2 + 2i]
= 2 – 2i
Question 2. For any two complex numbers z1 and z2, prove that, Re (z1z2) = Re z1 Re z2 – Im z1 Im z2
Solution:
Let’s assume z1 = x1 + iy1 and z2 = x2 + iy2 as two complex numbers
Product of these complex numbers, z1z2
z1z2 = (x1 + iy1)(x2 + iy2)
= x1(x2 + iy2) + iy1(x2 + iy2)
= x1x2 + ix1y2 + iy1x2 + i2y1y2
= x1x2 + ix1y2 + iy1x2 – y1y2 [i2 = -1]
= (x1x2 – y1y2) + i(x1y2 + y1x2)
Now,
Re(z1z2) = x1x2 – y1y2
⇒ Re(z1z2) = Rez1Rez2 – Imz1Imz2
Hence, proved.
Question 3. Reduce to the standard form 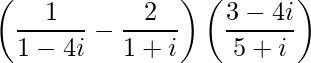
Solution:
![Rendered by QuickLaTeX.com \displaystyle\left(\frac{1}{1-4i}-\frac{2}{1+i}\right)\left(\frac{3-4i}{5+i}\right)=\left[\frac{(1+i)-2(1-4i)}{(1-4i)(1+i)}\right]\left[\frac{3-4i}{5+i}\right]\\ = \left[\frac{1+i-2+8i}{1+i-4i-4i^2}\right] \left[\frac{3-4i}{5+i}\right]= \left[\frac{-1+9i}{5-3i}\right] \left[\frac{3-4i}{5+i}\right]\\ = \left[\frac{-3+4i+27i-36i^2}{25+5i-15i-3i^2}\right]=\frac{33+31i}{28-10i}=\frac{33+31i}{2(14-5i)}\\ = \frac{(33+31i)}{2(14-5i)}\times\frac{14+5i}{14+5i}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c15226e112c8e1996a8c7eea62f4e566_l3.png)
On multiplying numerator and denominator by (14+5i)
![Rendered by QuickLaTeX.com \\ =\frac{462+165i+434i+155i^2}{2[(14)^2-(5i)^2]}=\frac{307+599i}{2(196-25i^2)}\\ =\frac{307+599i}{2(221)}=\frac{307+599i}{442}=\frac{307}{442}+\frac{599i}{442}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b76cc1fad43040e25508228c57b7cdf9_l3.png)
Hence, this is the required standard form.
Question 4. If x – iy = 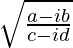 prove that (x2 + y2)2
prove that (x2 + y2)2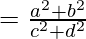
Solution:
Given:
x – iy = 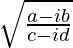

On multiplying numerator and denominator by (c+id)
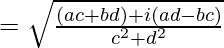
So,
(x – iy)2 = 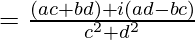
x2 – y2 – 2ixy 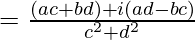
On comparing real and imaginary parts, we get
x2 – y2 =  , -2xy =
, -2xy = 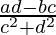 (1)
(1)
(x2 + y2)2 = (x2 – y2)2 + 4x2y2
= 
Hence proved
Question 5. Convert the following in the polar form:
(i) 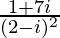
(ii) 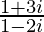
Solution:
(i) Here, z = 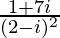
= 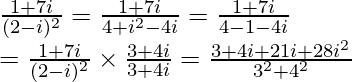
Multiplying by its conjugate in the numerator and denominator
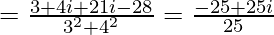
= -1+i
Let r cos θ = -1 and r sin θ = 1
On squaring and adding, we get
r2 (cos2θ + sin2θ) = 1 + 1 = 2
r2 = 2 [cos2θ + sin2θ = 1]
r = √2
So,
√2 cosθ = -1 and √2 sinθ = 1
⇒ cosθ = 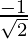 and sinθ =
and sinθ = 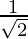
Therefore,
θ = 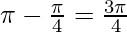 [As θ lies in II quadrant]
[As θ lies in II quadrant]
Expressing as, z = r cos θ + i r sin θ
= 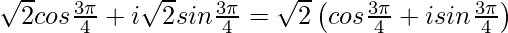
Therefore, this is the required polar form.
(ii) Let, z = 
= -1 + i
Now, Let r cosθ = -1 and r sin θ = 1
On squaring and adding, we get
r2(cos2θ + sin2θ) = 1 + 1
r(cos2θ + sin2θ) = 2
r2 = 2 [cos2θ + sin2θ = 1]
= r = √2 [Conventionally, r > 0]
Therefore,
√2 cosθ = -1 and √2 sinθ = 1
cosθ = 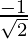 and sinθ =
and sinθ = 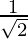
Therefore,
θ = 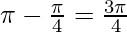 [As θ lies in II quadrant]
[As θ lies in II quadrant]
Expressing as, z = r cosθ + i r sinθ
z = 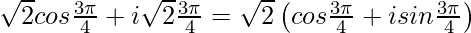
Therefore, this is the required polar form.
Solve each of the equation in Exercises 6 to 9.
Question 6. 3x2 – 4x + 20/3 = 0
Solution:
Given quadratic equation, 3x2 – 4x + 20/3 = 0
It can be re-written as: 9x2 – 12x + 20 = 0
On comparing it with ax2 + bx + c = 0, we get
a = 9, b = –12, and c = 20
So, the discriminant of the given equation will be
D = b2 – 4ac = (–12)2 – 4 × 9 × 20 = 144 – 720 = –576
Hence, the required solutions are
X = 
Question 7. x2 – 2x + 3/2 = 0
Solution:
Given:
Quadratic equation, x2 – 2x + 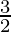 = 0
= 0
After re-written 2x2 – 4x + 3 = 0
On comparing it with ax2 + bx + c = 0,
We get
a = 2, b = –4, and c = 3
So, the discriminant of the given equation will be
D = b2 – 4ac = (–4)2 – 4 × 2 × 3 = 16 – 24 = –8
Hence, the required solutions are
x = ![Rendered by QuickLaTeX.com \frac{-b\pm\sqrt{D}}{2a}=\frac{-(-4)\pm\sqrt{-8}}{2\times2}=\frac{4\pm2\sqrt2i}{4}\ \ \ \ [\sqrt{-1}=i]\\ =\frac{2\pm\sqrt2i}{2}=1\pm\frac{\sqrt2}{2}i](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-891d07c7751cd344a36d72a9695b3a00_l3.png)
Question 8. 27x2 – 10x + 1 = 0
Solution:
Given:
Quadratic equation, 27x2 – 10x + 1 = 0
On comparing it with ax2 + bx + c = 0,
We get
a = 27, b = –10, and c = 1
So, the discriminant of the given equation will be
D = b2 – 4ac = (–10)2 – 4 × 27 × 1 = 100 – 108 = –8
Hence, the required solutions are

Question 9. 21x2 – 28x + 10 = 0
Solution:
Given:
Quadratic equation, 21x2 – 28x + 10 = 0
On comparing it with ax2 + bx + c = 0,
We have
a = 21, b = –28, and c = 10
So, the discriminant of the given equation will be
D = b2 – 4ac = (–28)2 – 4 × 21 × 10 = 784 – 840 = –56
Hence, the required solutions are
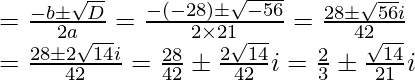
Question 10. If z1 = 2 – i, z2 = 1 + i, find 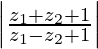
Solution:
Given, z1 = 2 – i, z2 = 1 + i
![Rendered by QuickLaTeX.com \left|\frac{z_1+z_2+1}{z_1-z_2+1}\right|=\left|\frac{(2-i)+(1+i)+1}{(2-i)-(1+i)+1}\right|\\ =\left|\frac{4}{2-2i}\right|=\left|\frac{4}{2(1-i)}\right|\\ =\left|\frac{2}{1-i}\times\frac{1+i}{1+i}\right|=\left|\frac{2(1+i)}{1^2-i^2}\right|\\ =\left|\frac{2(1+i)}{1+1}\right|\ \ \ \ \ [i^2=-1]\\ =\left|\frac{2(1+i)}{2}\right|\\ =|1+i|=\sqrt{1^2+1^2}=\sqrt2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6c409c10a79cb7ac251f186e0fffa7aa_l3.png)
Hence, the value of 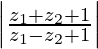 is √2
is √2
Share your thoughts in the comments
Please Login to comment...