Class 11 RD Sharma Solutions – Chapter 30 Derivatives – Exercise 30.4 | Set 2

Last Updated : 16 May, 2021

Question 11. Differentiate (x sin x + cos x) (x cos x − sin x) with respect to x.

Solution:

We have,
=> y = (x sin x + cos x) (x cos x − sin x)
On differentiating both sides, we get,
$\frac{dy}{dx}=\frac{d}{dx}[(x sin x + cos x) (x cos x − sin x)]$
On using product rule we get,
= $(xcosx−sinx)\frac{d}{dx}(xsinx+cosx)+(xsinx+cosx)\frac{d}{dx}(xcosx-sinx)$
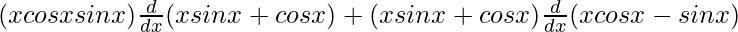
On using chain rule, we get,
= $(xcosx−sinx)\left[\frac{d}{dx}(xsinx)+\frac{d}{dx}(cosx)\right]+(xsinx+cosx)\left[\frac{d}{dx}(xcosx)-\frac{d}{dx}(sinx)\right]$
On using product rule again, we get,
= $(xcosx−sinx)\left[sinx\frac{d}{dx}(x)+x\frac{d}{dx}(sinx)-sinx\right]+(xsinx+cosx)\left[cosx\frac{d}{dx}(x)+x\frac{d}{dx}(cosx)-cosx\right]$
= $(xcosx−sinx)\left[sinx+xcosx-sinx\right]+(xsinx+cosx)\left[cosx-xsinx-cosx\right]$
= (x cos x − sin x) (x cos x) + (x sin x + cos x) (−x sin x)
= x² cos² x − x cos x sin x − x² sin² x − x cos x sin x
= x² (cos² x − sin² x) − 2x cos x sin x
= x² cos 2x − x sin 2x
= x (x cos 2x − sin 2x)

Question 12. Differentiate (x sin x + cos x) (e^x + x² log x) with respect to x.

Solution:

We have,
=> y = (x sin x + cos x) (e^x + x² log x)
On differentiating both sides, we get,
$\frac{dy}{dx}=\frac{d}{dx}[(x sin x + cos x) (e^x + x^2 log x)]$
On using product rule we get,
= $(e^x + x^2 log x)\frac{d}{dx}(x sin x + cos x)+(x sin x + cos x)\frac{d}{dx}(e^x + x^2 log x)$
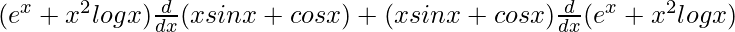
On using chain rule, we get,
= $(e^x + x^2 log x)\left[\frac{d}{dx}(x sin x)+\frac{d}{dx}(cos x)\right]+(x sin x + cos x)\left[\frac{d}{dx}(e^x) + \frac{d}{dx}(x^2 log x)\right]$
On using product rule again, we get,
= $(e^x+x^2log x)\left[sinx\frac{d}{dx}(x)+x\frac{d}{dx}(sinx)-sinx\right]+(xsinx+cosx)\left[e^x+logx\frac{d}{dx}(x^2)+x^2\frac{d}{dx}(logx)\right]$
= $(e^x+x^2log x)\left[sinx+xcosx-sinx\right]+(xsinx+cosx)\left[e^x+2xlogx+x^2(\frac{1}{x})\right]$
= $(e^x+x^2log x)\left(xcosx\right)+(xsinx+cosx)\left[e^x+2xlogx+x\right]$
= (x cos x) (e^x+ x²log x) +(x sin x + cos x) (e^x+ 2x log x + x)

Question 13. Differentiate (1 − 2 tan x) (5 + 4 sin x) with respect to x.

Solution:

We have,
=> y = (1 − 2 tan x) (5 + 4 sin x)
On differentiating both sides, we get,
$\frac{dy}{dx}=\frac{d}{dx}[(1−2tanx)(5+4sinx)]$
On using product rule we get,
= $(5+4sinx)\frac{d}{dx}(1−2tanx)+(1-2tanx)\frac{d}{dx}(5+4sinx)$
= $(5+4sinx)(−2sec^2x)+(1-2tanx)(4cosx)$
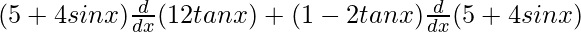
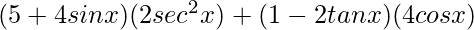
= −10 sec² x − 8 sin x sec² x + 4 cos x − 8 tan x cos x
= $−10sec^2x−8sinx(\frac{1}{cos^2x})+4cosx−8(\frac{sinx}{cosx})cosx$
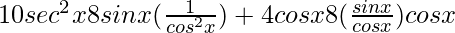
= −10 sec² x − 8 tan x sec x + 4 cos x − 8 sin x

Question 14. Differentiate (1 + x²) cos x with respect to x.

Solution:

We have,
=> y = (1 + x²) cos x
On differentiating both sides, we get,
$\frac{dy}{dx}=\frac{d}{dx}[(1 + x^2) cos x]$
On using product rule we get,
= $cosx\frac{d}{dx}[(1 + x^2)]+(1+x^2)\frac{d}{dx}(cosx)$
= cos x (2x) + (1 + x²) (−sinx)
= 2x cos x − sin x(1 + x²) (sinx)

Question 15. Differentiate sin²x with respect to x.

Solution:

We have,
=> y = sin² x
=> y = (sin x) (sin x)
On differentiating both sides, we get,
$\frac{dy}{dx}=\frac{d}{dx}[(sin x) (sin x)]$
On using product rule we get,
= $sinx\frac{d}{dx}(sinx)+(sinx)\frac{d}{dx}(sinx)$
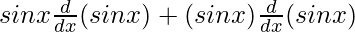
= sin x cos x + sin x cos x
= 2 sin x cos x
= sin 2x

Question 16. Differentiate 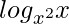$log_{x^2}x$ with respect to x.

Solution:

We have,
=> y = 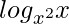$log_{x^2}x$
= $\frac{logx}{logx^2}$
= $\frac{logx}{2logx}$
= $\frac{1}{2}$
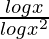
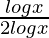
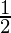
On differentiating both sides, we get,
$\frac{dy}{dx}=\frac{d}{dx}(\frac{1}{2})$
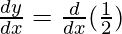
= 0

Question 17. Differentiate 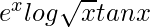$e^xlog\sqrt{x}tanx$ with respect to x.

Solution:

We have,
=> y = 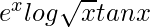$e^xlog\sqrt{x}tanx$
On differentiating both sides, we get,
$\frac{dy}{dx}=\frac{d}{dx}(e^xlog\sqrt{x}tanx)$
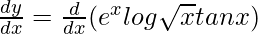
On using product rule we get,
= $log\sqrt{x}tanx\frac{d}{dx}(e^x)+e^x\frac{d}{dx}(log\sqrt{x}tanx)$
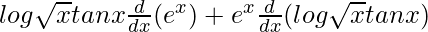
On using product rule again, we get,
= $log\sqrt{x}tanx(e^x)+e^x\left[tanx\frac{d}{dx}(log\sqrt{x})+log\sqrt{x}\frac{d}{dx}(tanx)\right]$
= $e^xlog\sqrt{x}tanx+e^x\left[tanx(\frac{1}{\sqrt{x}})(\frac{1}{2\sqrt{x}})+log\sqrt{x}sec^2x\right]$
= $e^xlog\sqrt{x}tanx+e^x\left[\frac{tanx}{2x}+log\sqrt{x}sec^2x\right]$
= $\frac{1}{2}e^xlogxtanx+e^x\left[\frac{tanx}{2x}+\frac{1}{2}logxsec^2x\right]$
= $\frac{e^x}{2}[logxtanx+\frac{tanx}{x}+logxsec^2x]$

Question 18. Differentiate x³ e^x cos x with respect to x.

Solution:

We have,
=> y = x³e^x cos x
On differentiating both sides, we get,
$\frac{dy}{dx}=\frac{d}{dx}(x^3e^xcosx)$
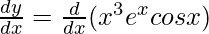
On using product rule we get,
= $e^xcosx\frac{d}{dx}(x^3)+x^3\frac{d}{dx}(e^xcosx)$
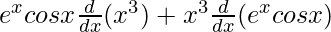
On using product rule again, we get,
= $e^xcosx(3x^2)+x^3[cosx\frac{d}{dx}(e^x)+e^x\frac{d}{dx}(cosx)]$
= $3x^2e^xcosx+x^3[e^xcosx-e^xsinx]$
= $3x^2e^xcosx+x^3e^xcosx-x^3e^xsinx$
= $x^2e^x(3cosx+xcosx-xsinx)$

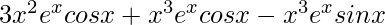
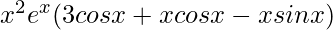
Question 19. Differentiate 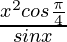$\frac{x^2cos\frac{\pi}{4}}{sinx}$ with respect to x.

Solution:

We have,
=> y = 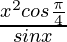$\frac{x^2cos\frac{\pi}{4}}{sinx}$
=> y = 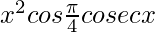$x^2cos\frac{\pi}{4}cosecx$
On differentiating both sides, we get,
$\frac{dy}{dx}=\frac{d}{dx}(x^2cos\frac{\pi}{4}cosecx)$
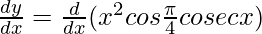
On using product rule we get,
= $cos\frac{\pi}{4}cosecx\frac{d}{dx}(x^2)+x^2\frac{d}{dx}(cos\frac{\pi}{4}cosecx)$
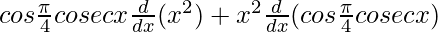
On using product rule again, we get,
= $cos\frac{\pi}{4}cosecx(2x)+x^2[cosecx\frac{d}{dx}(cos\frac{\pi}{4})+cos\frac{\pi}{4}\frac{d}{dx}(cosecx)]$
= $2xcos\frac{\pi}{4}cosecx+x^2[cosecx(0)+cos\frac{\pi}{4}(-cosecxcotx)]$
= $2xcos\frac{\pi}{4}cosecx+x^2[cos\frac{\pi}{4}(-cosecxcotx)]$
= $2xcos\frac{\pi}{4}cosecx-x^2cos\frac{\pi}{4}cosecxcotx$
= $2x(\frac{1}{\sqrt{2}})cosecx-x^2(\frac{1}{\sqrt{2}})cosecxcotx$
= $\frac{xcosecx}{\sqrt{2}}(2-xcotx)$

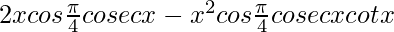
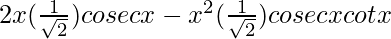
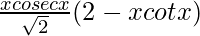
Question 20. Differentiate x⁴ (5 sin x − 3 cos x) with respect to x.

Solution:

We have,
=> y = x⁴ (5 sin x − 3 cos x)
On differentiating both sides, we get,
$\frac{dy}{dx}=\frac{d}{dx}[x^4(5sinx−3cosx)]$
On using product rule we get,
= $(5sinx−3cosx)\frac{d}{dx}(x^4)+x^4\frac{d}{dx}(5sinx−3cosx)$
= $(5sinx−3cosx)(4x^3)+x^4(5cosx+3sinx)$
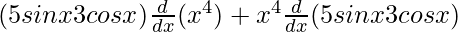
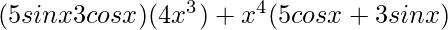
= 20 x³ sin x − 12 x³ cos x + 5x⁴ cos x + 3x⁴ sin x