Class 11 RD Sharma Solutions – Chapter 16 Permutations – Exercise 16.3 | Set 2
Last Updated :
28 Jan, 2021
Question 11. If P(n, 5) : P(n, 3) = 2 : 1, find n.
Solution:
Given:
P(n, 5) : P(n, 3) = 2 : 1
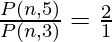
After applying the formula,
P (n, r) = 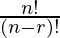
P (n, 5) = 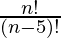
P (n, 3) = 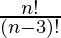
So, from the question,
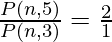
After substituting the values in above expression we will get,
![Rendered by QuickLaTeX.com \frac{\frac{n!}{(n-5)!}}{\frac{n!}{(n-3)!}}=\frac{2}{1}\\ \frac{n!}{(n-5)!}\times\frac{(n-3)!}{n!}=\frac{2}{1} \\\frac{(n - 3)! }{ (n - 5)!} = \frac{2}{1}\\ \frac{[(n - 3) (n - 3 - 1) (n - 3 - 2)!] }{ (n - 5)!} = \frac{2}{1}\\ \frac{[(n - 3) (n - 4) (n - 5)!]} { (n - 5)!} = \frac{2}{1}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4100bc5754b9cf07fe343e5a48c34ddb_l3.png)
(n – 3)(n – 4) = 2
n2 – 3n – 4n + 12 = 2
n2 – 7n + 12 – 2 = 0
n2 – 7n + 10 = 0
n2 – 5n – 2n + 10 = 0
n (n – 5) – 2(n – 5) = 0
(n – 5) (n – 2) = 0
n = 5 or 2
For, P (n, r): n ≥ r
∴ n = 5 [for, P (n, 5)]
Question 12. Prove that:
1. P (1, 1) + 2. P (2, 2) + 3 . P (3, 3) + … + n . P(n, n) = P(n + 1, n + 1) – 1.
Solution:
By using the formula,
P (n, r) = 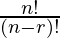
P (n, n) = 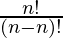
=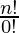
= n! [Since, 0! = 1]
Consider LHS:
= 1. P(1, 1) + 2. P(2, 2) + 3. P(3, 3) + … + n . P(n, n)
= 1.1! + 2.2! + 3.3! +………+ n.n! [Since, P(n, n) = n!]

= (2! – 1!) + (3! – 2!) + (4! – 3!) + ……… + (n! – (n – 1)!) + ((n+1)! – n!)
= 2! – 1! + 3! – 2! + 4! – 3! + ……… + n! – (n – 1)! + (n+1)! – n!
= (n + 1)! – 1!
= (n + 1)! – 1 [Since, P (n, n) = n!]
= P(n+1, n+1) – 1
= RHS
Hence Proved.
Question 13. If P(15, r – 1) : P(16, r – 2) = 3 : 4, find r.
Solution:
Given:
P(15, r – 1) : P(16, r – 2) = 3 : 4
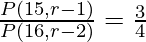
After applying the formula,
P (n, r) = 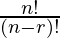
P (15, r – 1) = 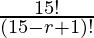
= 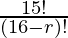
P (16, r – 2) = 
= 
So, from the question,
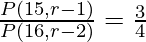
After substituting the values in above expression we will get,
![Rendered by QuickLaTeX.com \frac{\frac{15!}{(16-r)!}}{\frac{16!}{(18-r)!}}=\frac{3}{4}\\ \frac{15! }{ (16 - r)!} × \frac{(18 - r)! }{ 16!} = \frac{3}{4}\\ \frac{15! }{ (16 - r)!} × \frac{[(18 - r) (18 - r - 1) (18 - r - 2)!]}{(16×15!)} = \frac{3}{4}\\ \frac{1}{(16 - r)!} × \frac{[(18 - r) (17 - r) (16 - r)!]}{16} = \frac{3}{4}\\ (18 - r) (17 - r) = \frac{3}{4} × 16\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-39fac7143003a909f3a1af4ef91aaca6_l3.png)
(18 – r) (17 – r) = 12
306 – 18r – 17r + r2 = 12
306 – 12 – 35r + r2 = 0
r2 – 35r + 294 = 0
r2 – 21r – 14r + 294 = 0
r(r – 21) – 14(r – 21) = 0
(r – 14) (r – 21) = 0
r = 14 or 21
For, P(n, r): r ≤ n
∴ r = 14 [for, P(15, r – 1)]
Question 14. n+5Pn+1 = 11(n – 1)/2 n+3Pn, find n.
Solution:
Given:
n+5Pn+1 = 11(n – 1)/2 n+3Pn
P (n +5, n + 1) = 11(n – 1)/2 P(n + 3, n)
By using the formula,
P (n, r) = 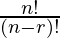
P(n + 5, n=1) = 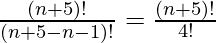
P(n + 3, n) = 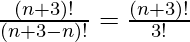
So, from the question
P(n + 5, n + 1) = 11(n -1)/2P(n + 3, n)
After substituting the values in above expression we get,
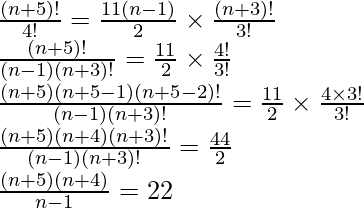
(n + 5) (n + 4) = 22 (n – 1)
n2 + 4n + 5n + 20 = 22n – 22
n2 + 9n + 20 – 22n + 22 = 0
n2 – 13n + 42 = 0
n2 – 6n – 7n + 42 = 0
n(n – 6) – 7(n – 6) = 0
(n – 7) (n – 6) = 0
n = 7 or 6
∴ The value of n can either be 6 or 7.
Question 15. In how many ways can five children stand in a queue?
Solution:
Number of arrangements of ‘n’ things taken all at a time = P (n, n)
Hence,
After applying the formula,
P (n, r) = 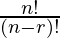
The total number of ways in which five children can stand in a queue = the number of arrangements of 5 things taken all at a time = P (5, 5)
Thus,
P (5, 5) = 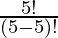
= 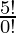
= 5! [Since, 0! = 1]
= 5 × 4 × 3 × 2 × 1
= 120
Therefore, Number of ways in which five children can stand in a queue are 120.
Question 16. From among the 36 teachers in a school, one principal and one vice-principal are to be appointed. In how many ways can this be done?
Solution:
Given:
The total number of teachers in a school = 36
As we know that, number of arrangements of n things taken r at a time = P(n, r)
After applying the formula,
P (n, r) = 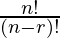
∴ The total number of ways in which this can be done = the number of arrangements of 36 things taken 2 at a time = P(36, 2)
P (36, 2) = 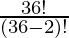
= 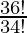
= 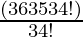
= 36 × 35
= 1260
Hence, Number of ways in which one principal and one vice-principal are to be appointed out of total 36 teachers in school are 1260.
Share your thoughts in the comments
Please Login to comment...