Slope of a Line is the measure of the steepness of a line or a surface or a curve whichever is the point of consideration. The slope of a Line is a fundamental concept in the stream of calculus or coordinate geometry or we can say the slope of a line is fundamental to the complete mathematics subject. The understanding of slope helps us solve many problems in mathematics, physics, or engineering.
In this article, we will learn about the slope of a line in detail, slope of a straight line with its various methods of calculations, and also the equation for the slope of a line.
What is a Slope?
In mathematics, the slope is the measure of the steepness of a line or a surface which means the slope of a line tells us how steep a line or surface is inclined with the positive x-axis. The higher the slope of a curve or a line, the greater the amount of steepness it will show in the graph. Generally, the slope is defined in two-dimensional coordinates as the ratio of the change in the y-coordinate with respect to the change in the x-coordinate.
What is the Slope of a Line?
Similar to the general slope, the slope of a line or the slope of a straight line is the measure of the steepness of a line and is mathematically given as the ratio of the change in the y-coordinate to the change in the x-coordinate of the line. Other than this mathematical interpretation, the slope has a physical interpretation that tells us about the line that is in which direction the line will tilt. A higher positive slope shows less tilt in the positive x direction and a lower positive slope shows a higher tilt in the positive x direction. For the negative slope, the higher the absolute value of the negative slope higher the tilt towards the negative x direction.
The formula of the slope is given by the ratio of change in the y coordinate to the change in the x coordinate, which can be written mathematically can as
Slope = Change in y coordinate/Change in x coordinate = Δy/Δx
If the inclination of the line with a positive x-axis is θ, then the slope is given as follows:
m = tan θ
Slope of a Line Equation
The slope of a line is given as
y – y1 = m(x – x1)
⇒ y = mx + C where m is slope and C is intercept
How to find the Slope of a Line?
There are various methods to find the slope of any line, which can be used appropriately on the basis of the given conditions. These methods are:
- Calculation of Slope between Two Points
- Calculation of Slope from Graph
- Calculation of Slope from Table
Calculation of Slope between Two Points
If the given points are (x1, y1) and (x2, y2) then the slope of a line passing through both points is given by:
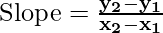
Example: Find the point of the slope if points are (4, 2) and (8, 12).
Answer:
Given: Point A (4,2) and point B (8,12)
Coordinate x1 and y1 is 4 and 2
Coordinate x2 and y2 is 8 and 12
Thus, 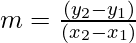
⇒ m = (12 – 2)/(8 – 4)
⇒ m = 10/4 = 2.5
Calculation of Slopes from Graph
Calculation of the slope from a Graph can be achieved using the following steps:
Step 1: Mark two points on the line with their coordinates.
Step 2: Use the Formula for the Slope between two points to calculate the slope.
Example: Find the slope of the following line in the graph.
Solution:
We have to find Δx and Δy (change in x and change in y)
So, change in Δx is 6 and change is Δy -3
Now slope m is given as follows:
m = Δy/Δx
⇒ m = 6/-3 = -2
Calculation of Slope from Table
Calculation of the Slope from the Table can be done using the following steps:
Step 1: Choose two values of x and its corresponding values of y from the table.
Step 2: Calculate the change in x value and change in y value.
Step 3: Calculate the slope using the formula, Slope = change in y-values/change in x-values.
Example 1: Calculate the slope between x = 1 and x = 3 of the following table.
Answer:
Change in x-values = 3 – 1 = 2
Change in y-values = 9 – 5 = 4
As we know, Slope = change in y-values/change in x-values
⇒ Slope = 4/2 = 2
So, the slope between x=1 and x=3 in this table is 2.
Example 2: Calculate the slope of the following table.
Solution:
Identify change in each consecutive pair of y so change in the y is 5, 5 and 5.
Identify change in each consecutive pair of x so change in the x is 1, 1 and 1.
Now writing the ratio using slope formula 5/1, 5/1 and 5/1.
So, slope from table is 5.
Positive and Negative Slope
A line is said to have a positive slope if it is making less than the right angle with the positive x-axis and a line is said to have a negative slope if it makes more than the right angle with the positive x-axis. In other words, a line with a positive slope looks tilted forward in the direction of the positive x-axis, and a line with a negative slope looks tilted backward in the direction of the negative y-axis.
Slopes of Different Lines
There can be various different lines that can be named such as:
- Horizontal Line
- Vertical Line
- Perpendicular Lines
- Parallel Lines
Let’s discuss the Slope of these various different lines as follows:
Slope of Horizontal Line
The line that is parallel to the x-axis is called a horizontal line and the slope of a Horizontal Line is 0 as there is no change in the y-coordinate throughout the line for any change in the x-coordinate. Since the slope of the Horizontal Line is Zero, it is also called a Zero Slope line. Thus mathematically we can represent this as:
Slope of Horizontal Line = 0/change in x-coordinate = 0
Slope of Vertical Line
The line parallel to the y-axis is called a vertical line and the slope of a Vertical Line is not defined as there is no change in the x-coordinate throughout the line for any change in the y-coordinate. The Vertical Line is also called Undefined Slope Line. Thus mathematically we can represent this as:
Slope of Vertical Line = Change in y-coordinate/0 = Not Defined
Slope of Perpendicular Lines
The slope of Perpendicular Lines are inversely proportional to each other and their product is -1. In other words, if we have two lines with slopes m1 and m2, then the condition for those two lines to be perpendicular is:
m1 = -1/m2
OR
m1 × m2 = -1
Slope of Parallel Lines
The slope of Parallel Lines is the same as both the lines are at the same inclined with the positive x-axis. In other words, if the slope of one line is m then the slope of a line parallel to that line is also m.
The equation of a line in the slope-intercept form is given as follows:
y = mx + c
Where,
- m is the slope of the line, and
- c is the y-intercept cut by the line.
Equation of Line Using Slope
If a line is passing through a point (x1, y1) and its slope is m, then the equation of a line is given as follows:
y – y1 = m(x – x1)
Where x and y represent all the coordinates of the line.
We can also write the same equation using the two points from which the line is passing. If the line passes through (x1, y1) and (x2, y2) then its equation is given by:
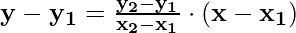
Example 1: Find the equation of a line given in the graph.
Answer:
Slope of the graph is, m = 8/2 = 4
and we know the equation of line passing through (x1, y1) with slope m is given by
y – y1 = m (x – x1)
Thus, equation of line (4,2) with slope 4 is
y – 2 = 4 (x – 4)
⇒ y – 2 = 4x – 16
⇒ y = 4x – 16 +2
⇒ y = 4x – 14
Example 2: Find the equation of the line given in the graph.
Answer:
Two given points (x1, y1) and (x2, y2) are A (2,3) and B (5,7)
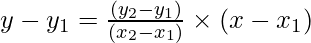
⇒ y-3= {(7 -3)/(5-2)} (x-2)
⇒ 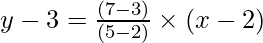
⇒ 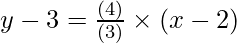
⇒ 3y-9 = 4x-8
⇒ 3y = 4x+1
The equation of the line whose length of the perpendicular from the origin is p and the angle made by the perpendicular with the positive x-axis is given by α is given by:
x cos α + y sin α = p
This is known as the normal form of the line.
In the case of the general form of the line Ax + By + C = 0 can be represented in normal form as:
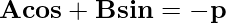
From this we can say that  and
and 
Also, it can be inferred that,
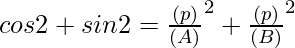
⇒ 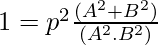
⇒ 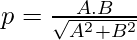
From the general equation of a straight-line Ax + By + C = 0, we can conclude the following:
- The slope is given by -A/B, given that B ≠ 0.
- The x-intercept is given by -C/A and the y-intercept is given by -C/B.
- It can be seen from the above discussion that:
- If two points (x1, y1) and (x2, y2) are said to lie on the same side of the line Ax + By + C = 0, then the expressions Ax1+ By1 + C and Ax2 + By2 + C will have the same sign or else these points would lie on the opposite sides of the line.
Angle between Two Lines
When two lines with slopes m1 and m2 intersect they form angles. The relation between the slope of the intersecting lines and the angle so formed is given as follows:
tanθ = 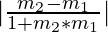
if 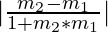 > 0, acute angle is formed between the lines
> 0, acute angle is formed between the lines
if 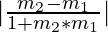 < 0, obtuse angle is formed between the lines
< 0, obtuse angle is formed between the lines
Read More,
Sample Problems on Slope of a Line
Problem 1: Find the slope of points (1,2) and (2,3).
Solution:
As slope is given as m = (y2 – y1)/(x2 – x1)
⇒ m = (3 – 2)/(2 – 1)
⇒ m = 1
Problem 2: Find the value of x if the slope is 2 and points are (2,2) and (x,6).
Solution:
m = (y2 – y1)/(x2 – x1)
⇒ 2 = (6 – 2)/(x – 2)
⇒ 4 = 2(x-2)
⇒ x-2 = 2
⇒ x = 4
Problem 3: Find the value of y if slope is 3 and points are (2,13) and (4, y).
Solution:
m = (y2 – y1)/(x2 – x1)
⇒ 3 = (y – 13)/(4 – 2)
⇒ y – 13 = 3(2)
⇒ y – 13 = 6
⇒ y = 6 + 13 = 19
Problem 4: Find the line passing from coordinates (2,5) and the slope of a line is 5.
Solution:
Slope m = 4
y – y1= m (x – x1)
We know slope m = 5 and point (x1, y1) = (2,5)
Now putting these value in equation
⇒ y – 5 = 5 x (x – 2)
⇒ y – 5 = 5x – 10
⇒ y = 5x – 10 + 5
⇒ y = 5x -5
FAQs on Slope of a Line
1. What is the Slope of a Line?
Slope is the measure of the steepness of a line which tells us how much a line is inclined with the positive x-axis.
2. What is the slope of a straight line?
Slope of a straight line is same as slope of a line. As a line is always a straight line.
3. How is the Slope of a Line calculated?
To calculate the slope of a line, we just need to take two point on the line and calculate the ratio of change in y-coordinate to change in x-coordinate.
4. What does a Positive and Negative Slope represent?
Positive Slope represents that graph is increasing in nature while Negative Slope represents that in graph line is going down from left to right.
5. Can the Slope of a Line be greater than 1?
Yes slope of a line can be greater than 1, as one of the formula for is slope m = tan θ, and range of tan θ is the complete set of real numbers.
6. What is the Slope-Intercept form of a Line?
The slope-intercept form of a line is given as follows:
y = mx + c
Where,
- m is the slope of the line, and
- c is the y-intercept cut by the line.
7. What is the Point-Slope form of a Line?
The point slope form is called point slope form, as it is defined as a line is passing through a point (x1, y1) and its slope is m, and is given by:
y – y1 = m(x – x1)
Share your thoughts in the comments
Please Login to comment...