Question 1. Find a, b, and n in the expansion of (a + b)n if the first three terms of the expansion are 729, 7290, and 30375, respectively.
Solutions:
As, we know that (r+1)th term of (a+b)n is denoted by,
Tr+1 = nCr an-r br
Here, it is given that first three terms of the expansion are 729, 7290 and 30375.
When, T1 = 729, T2 = 7290 and T3 = 30375
T0+1 (r=0) = nC0 an-0 b0 = an = 729 …………………(1)
T1+1 (r=0) = nC1 an-1 b1 = nan-1 b = 7290 …………………(2)
T2+1 (r=0) = nC2 an-2 b2 = 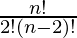 an-2b2 =
an-2b2 = 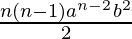 = 30375 …………………(3)
= 30375 …………………(3)
Dividing (1) and (2), we get
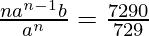
nan-1-n b = 10
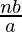 = 10 ……………………….(I)
= 10 ……………………….(I)
Now, dividing (3) and (2), we get
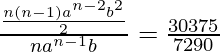
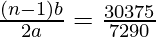
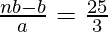

From (I), we can substitute
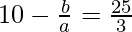
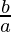 = 10 –
= 10 – 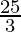
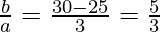 ………………….(II)
………………….(II)
Substituting (II) in (I), we get
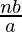 = 10
= 10
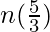 = 10
= 10
n = 
n = 6
Substituting n = 6 in (1), we get
an = 729
a6 = 729
a = 3
Substituting a = 3 in (II), we get
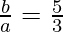
b = 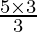
b = 5
Hence, a = 3, b = 5 and n = 6
Question 2. Find a if the coefficients of x2 and x3 in the expansion of (3 + ax)9 are equal.
Solutions:
As, we know that (r+1)th term of (a+b)n is denoted by,
Tr+1 = nCr an-r br
Here, a = 3 and b = ax and n = 9.
Tr+1 = 9Cr 39-r (ax)r
Tr+1 = 9Cr 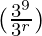 arxr
arxr
Tr+1 = 9Cr 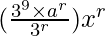
So, here if you want the power of x2 and x3. Then r=2 and r=3.
r = 2, T2+1 = ![Rendered by QuickLaTeX.com [^9C_2 (\frac{3^9 \times a^2}{3^2})] x^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-20dfa1e11b9353c10aa8746fdd8a0a39_l3.png)
r = 3, T3+1 = ![Rendered by QuickLaTeX.com [^9C_3 (\frac{3^9 \times a^3}{3^3})] x^3](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-72eb8e5a7372b8c71862884f05f483df_l3.png)
Coefficient of x2 = Coefficient of x3
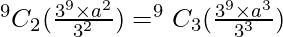

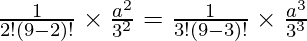
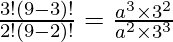

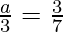
a = 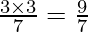
Hence, a = 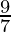
Question 3. Find the coefficient of x5 in the product (1 + 2x)6 (1 – x)7 using binomial theorem.
Solutions:
For getting the coefficient of x5, lets expand both the binomials for more clear understanding.
(1 + 2x)6 = 6C0 + 6C1 (2x) + 6C2 (2x)2 + 6C3 (2x)3 + 6C4 (2x)4 + 6C5 (2x)5 + 6C6 (2x)6
= 1 + 6 (2x) + 15 (2x)2 + 20 (2x)3 + 15 (2x)4 + 6 (2x)5 + (2x)6
= 1 + 12 x + 60x2 + 160 x3 + 240 x4 + 192 x5 + 64x6
(1 – x)7 = 7C0 – 7C1 (x) + 7C2 (x)2 – 7C3 (x)3 + 7C4 (x)4 – 7C5 (x)5 + 7C6 (x)6 – 7C7 (x)7
= 1 – 7x + 21x2 – 35x3 + 35x4 – 21x5 + 7x6 – x7
Now, the product will be seen as follows
(1 + 2x)6 (1 – x)7 = (1 + 12 x + 60x2 + 160 x3 + 240 x4 + 192 x5 + 64x6) (1 – 7x + 21x2 – 35x3 + 35x4 – 21x5 + 7x6 – x7)
Here, what we can see that x5 will be obtained when two terms will be multiplied of having sum of power of x as 5. Those two terms will be as follows:
| First binomial | Second binomial |
|---|
| 1st term | 6th term |
| 2nd term | 5th term |
| 3rd term | 4th term |
| 4th term | 3rd term |
| 5th term | 2nd term |
| 6th term | 1st term |
So,
Coefficient of x5 = (1)(-21) + (12)(35) + (60)(-35) + (160)(21) + (240)(-7) + (192)(1)
Coefficient of x5 = -21 + 420 – 2100 + 3360 – 1680 + 192
Coefficient of x5 = -21 + 420 – 2100 + 3360 – 1680 + 192
Coefficient of x5 = 171
Hence, the coefficient of x5 in the expression (1+2x)6 (1-x)7 is 171.
Question 4. If a and b are distinct integers, prove that a – b is a factor of an – bn, whenever n is a positive integer.
[Hint write an = (a – b + b)n and expand]
Solutions:
To prove that (a – b) is a factor of (an – bn),
an – bn = k (a – b) where k is some natural number or constant.
a can be written as = a – b + b
an = (a – b + b)n = [(a – b) + b]n
[(a – b) + b]n = nC0 (a – b)n + nC1 (a – b)n-1 b + ……….nCn-1(a – b)bn-1 + nCn bn
an = (a – b)n + n (a – b)n-1 b + ……….nCn-1(a – b)bn-1 + bn
Now, an – bn will be
an – bn = [(a – b)n + n (a – b)n-1 b + ……….nCn-1(a – b)bn-1 + bn] – bn
an – bn = (a – b)n + n (a – b)n-1 b + ……….nCn-1(a – b)bn-1
Taking (a-b) common, we have
an – bn = (a – b) [(a –b)n-1 + n (a – b)n-2 b + …… + nCn-1 bn-1]
an – bn = (a – b) k
Where k = [(a –b)n-1 + n (a – b)n-2 b + …… + nCn-1 bn-1] is a natural number
Hence, it is proved a – b is a factor of an – bn, where n is a positive integer
Question 5. Evaluate (√3+√2)6−(√3−√2)6.
Solutions:
Using binomial theorem the expression (a + b)6 and (a – b)6, can be expanded as follows:
(a + b)6 = 6C0 a6 + 6C1 a5 b + 6C2 a4 b2 + 6C3 a3 b3 + 6C4 a2 b4 + 6C5 a b5 + 6C6 b6
(a – b)6 = 6C0 a6 – 6C1 a5 b + 6C2 a4 b2 – 6C3 a3 b3 + 6C4 a2 b4 – 6C5 a b5 + 6C6 b6
Now adding them,
(a + b)6 – (a – b)6 = 6C0 a6 + 6C1 a5 b + 6C2 a4 b2 + 6C3 a3 b3 + 6C4 a2 b4 + 6C5 a b5 + 6C6 b6 – [6C0 a6 – 6C1 a5 b + 6C2 a4 b2 – 6C3 a3 b3 + 6C4 a2 b4 – 6C5 a b5 + 6C6 b6]
(a + b)6 – (a – b)6 = 2[6C1 a5 b + 6C3 a3 b3 + 6C5 a b5]
Substituting a = √3 and b = √2, we get
(√3 + √2)6 – (√3 – √2)6 = 2 [6 (√3)5 (√2) + 20 (√3)3 (√2)3 + 6 (√3) (√2)5]
= 2 [54(√6) + 120 (√6) + 24 √6]
= 2 (√6) (198)
= 396 √6
Question 6. Find the value of 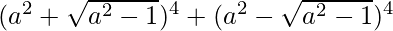 .
.
Solutions:
Using binomial theorem the expression (x+y)4 and (x – y)4, can be expanded as follows:
(x + y)4 = 4C0 x4 + 4C1 x3 y + 4C2 x2 y2 + 4C3 x y3 + 4C4 y4
(x – y)4 = 4C0 x4 – 4C1 x3 y + 4C2 x2 y2 – 4C3 x y3 + 4C4 y4
Now adding them,
(x + y)4 + (x – y)4 = 4C0 x4 + 4C1 x3 y + 4C2 x2 y2 + 4C3 x y3 + 4C4 y4 + [4C0 x4 – 4C1 x3 y + 4C2 x2 y2 – 4C3 x y3 + 4C4 y4]
(x + y)4 + (x – y)4 = 2[4C0 x4 + 4C2 x2 y2 + 4C4 y4]
Substituting x = a2 and y = 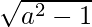 , we get
, we get
![Rendered by QuickLaTeX.com (a^2 + \sqrt{a^2-1})^4 + (a^2 - \sqrt{a^2-1})^4 = 2[(a^2)^4 +6 (a^2)^2 (\sqrt{a^2-1})^2 + (\sqrt{a^2-1})^4]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6a105cf51e901119088f8e9b031e38b2_l3.png)
= 2[a8 + 6a4 (a2-1) + (a2-1)2]
= 2[a8 + 6a6 – 6a4 + (a4 + 1 – 2(a2)(1))]
= 2[a8 + 6a6 – 6a4 + a4 + 1 – 2a2]
= 2a8 + 12a6 – 10a4 – 4a2 + 2
Question 7. Find an approximation of (0.99)5 using the first three terms of its expansion.
Solutions:
To make 0.99 in binomial form,
0.99 = 1 – 0.01
Now by applying binomial theorem, we get
(0. 99)5 = (1 – 0.01)5
Taking first three terms of its expansion, we have
= 5C0 (1)5 – 5C1 (1)4 (0.01) + 5C2 (1)3 (0.01)2
= 1 – 5 (0.01) + 10 (0.01)2
= 1 – 0.05 + 0.001
= 0.951
Approximation of (0.99)5 = 0.951.
Question 8. Find n, if the ratio of the fifth term from the beginning to the fifth term from the end in the expansion of ![Rendered by QuickLaTeX.com (\sqrt[4]{2} + \frac{1}{\sqrt[4]{3}})^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d349518c28e352011d60762b42f7cca_l3.png) is √6:1.
is √6:1.
Solutions:
As, here it is said we have to calculate
(Fifth term from the beginning : Fifth term from the end) of the Binomial = ![Rendered by QuickLaTeX.com (\sqrt[4]{2} + \frac{1}{\sqrt[4]{3}})^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2c5aca7dfb97c713295102baf18fdb51_l3.png)
Instead of taking fifth term from the end, lets reverse the binomial term and take it from beginning.
Fifth term from the end of binomial ![Rendered by QuickLaTeX.com (\sqrt[4]{2} + \frac{1}{\sqrt[4]{3}})^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d349518c28e352011d60762b42f7cca_l3.png) = Fifth term from the beginning
= Fifth term from the beginning ![Rendered by QuickLaTeX.com (\frac{1}{\sqrt[4]{3}}+ \sqrt[4]{2})^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-27a9aad415ed89e622fa14e9f66b6229_l3.png)
Lets move further with this
As, we know that (r+1)th term of (a+b)n is denoted by,
Tr+1 = nCr an-r br
Fifth term from the beginning of ![Rendered by QuickLaTeX.com (\sqrt[4]{2} + \frac{1}{\sqrt[4]{3}})^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d349518c28e352011d60762b42f7cca_l3.png) ,
,
T5 = T4+1 = nC4 ![Rendered by QuickLaTeX.com (\sqrt[4]{2})^{n-4} (\frac{1}{\sqrt[4]{3}})^4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f970d0e816df1e0990187f057ca646fa_l3.png)
T5 = nC4 ![Rendered by QuickLaTeX.com (\sqrt[4]{2})^n(\frac{1}{\sqrt[4]{2} \times \sqrt[4]{3}})^4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c51d30f8b138082068e764f77ec6f187_l3.png)
T5 = nC4 ![Rendered by QuickLaTeX.com (\sqrt[4]{2})^n (\frac{1}{2 \times 3})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-38ee9864292b20b649b0ee0f61858427_l3.png)
T5 = nC4 ![Rendered by QuickLaTeX.com (\frac{(\sqrt[4]{2})^n}{6})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9b9a69e27e28a6824c5dbfac4676a076_l3.png) …………………………….(1)
…………………………….(1)
Now, Fifth term from the beginning of ![Rendered by QuickLaTeX.com (\frac{1}{\sqrt[4]{3}}+ \sqrt[4]{2})^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-55c1f36a7b86b4268630c12dc1393dc8_l3.png) ,
,
T5 = T4+1 = nC4 ![Rendered by QuickLaTeX.com (\frac{1}{\sqrt[4]{3}})^{n-4} (\sqrt[4]{2})^4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-81d911d86d147f266daf8a25897eb46c_l3.png)
T5 = nC4 ![Rendered by QuickLaTeX.com \times \frac{(\frac{1}{\sqrt[4]{3}})^n}{(\frac{1}{\sqrt[4]{3}})^4} \times (2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6e604390cf60c8e8b1352eeb9fd6fde7_l3.png)
T5 = nC4 ![Rendered by QuickLaTeX.com \frac{(\frac{1}{\sqrt[4]{3}})^n}{(\frac{1}{3})} (2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-06e67170f950a7a259d429c553840d13_l3.png)
T5 = nC4 ![Rendered by QuickLaTeX.com (\frac{3}{(\sqrt[4]{3})^n}) (2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-020f70e256267076b312eefa962faddd_l3.png)
T5 = nC4 ![Rendered by QuickLaTeX.com (\frac{6}{(\sqrt[4]{3})^n})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aef99561f8ee29e45fbc626ccd98ed5b_l3.png) ……………………….(2)
……………………….(2)
Now taking ratio of (1) and (2), which is equal to √6:1
![Rendered by QuickLaTeX.com \frac{^nC_4 (\frac{(\sqrt[4]{2})^n}{6})}{^nC_4 (\frac{6}{(\sqrt[4]{3})^n})} = \sqrt{6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-27ba88ecd6c8511eb782a6e436e3e60d_l3.png)
![Rendered by QuickLaTeX.com \frac{(\sqrt[4]{2})^n \times (\sqrt[4]{3})^n}{(6\times 6)} = \sqrt{6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-25f92abf37b463bccddfbaadf2463578_l3.png)
![Rendered by QuickLaTeX.com (\sqrt[4]{6})^n = \sqrt{6} \times 36](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5ab818b29bed0b551fd4fa06636216b5_l3.png)
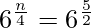
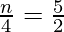
n = 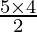
n = 10
Question 9. Expand using Binomial Theorem 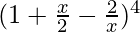 , x≠0.
, x≠0.
Solutions:
Grouping 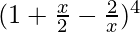 in binomial form, we have
in binomial form, we have
![Rendered by QuickLaTeX.com [(1+\frac{x}{2}) - \frac{2}{x}]^4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-55196ea84c1ef732e5795a08fc329046_l3.png)
Comparing it with (a+b)n,
a = 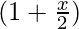 , b =
, b = 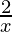 and n = 4
and n = 4
![Rendered by QuickLaTeX.com [(1+\frac{x}{2}) - \frac{2}{x}]^4](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f6b6376963d0fa574268264d3a7fb092_l3.png) = 4C0
= 4C0 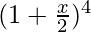 – 4C1
– 4C1 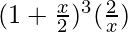 + 4C2
+ 4C2 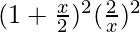 – 4C3
– 4C3 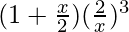 + 4C4
+ 4C4 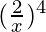
= 
= 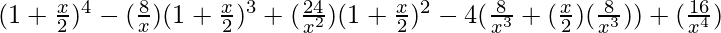
= 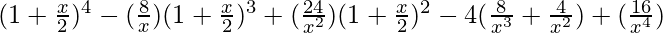
Now, lets get the value of 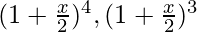 and
and 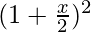

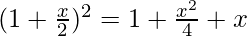
 = 3C0 (1)3 + 3C1 (1)2
= 3C0 (1)3 + 3C1 (1)2 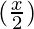 + 3C2 (1)
+ 3C2 (1) 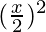 + 3C3
+ 3C3 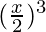

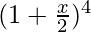 = 4C0 (1)4 + 4C1 (1)3
= 4C0 (1)4 + 4C1 (1)3 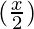 + 4C2 (1)2
+ 4C2 (1)2 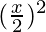 + 4C3 (1)
+ 4C3 (1) 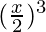 + 4C4
+ 4C4 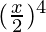
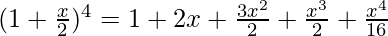
Now, substituting these values in the main equation, we get
= 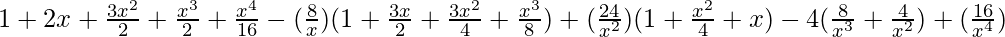
= 
= 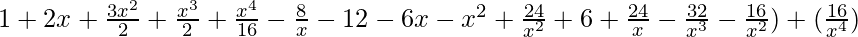
= 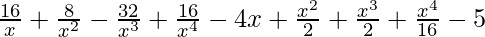
Question 10. Find the expansion of (3x2– 2ax + 3a2)3 using binomial theorem.
Solutions:
Grouping (3x2– 2ax + 3a2)3 in binomial form, we have
[3x2 + (- 2ax + 3a2)]3
Comparing it with (a+b)n,
a = 3x2, b = -a (2x-3a) and n = 3
[3x2 + (-a (2x-3a))]3
= 3C0 (3x2)3 + 3C1 (3x2)2 (-a (2x-3a)) + 3C2 (3x2) (-a (2x-3a))2 + 3C3 (-a (2x-3a))3
= 27x6 + 3 (9x4) (-a) (2x-3a) + 3 (3x2) (-a)2 (2x-3a)2 + (-a)3 (2x-3a)3
= 27x6 + (-54ax5 + 81a2x4) + 9a2x2 (2x-3a)2 – a3 (2x-3a)3
Now, lets get the value of (2x-3a)2 and (2x-3a)3.
(2x-3a)2 = (2x)2 + (3a)2 – 2(2x)(3a)
(2x-3a)2 = 4x2 + 9a2 -12xa
(2x-3a)3 = (2x)3 – (3a)3 – 3(2x)(3a)(2x-3a)
(2x-3a)3 = 8x3 – 27a3 – 36x2a +54xa2
Now, substituting these values in the main equation, we get
= 27x6 – 54ax5 + 81a2x4 + 9a2x2 (4x2 + 9a2 -12xa) – a3 (8x3 – 27a3 – 36x2a + 54xa2)
= 27x6 – 54ax5 + 81a2x4 + 36a2x4 + 81a4x2 -108x3a3 – (8a3x3 – 27a6 – 36x2a4 + 54xa5)
= 27x6 – 54ax5 + 117a2x4 + 81a4x2 -108x3a3 – 8a3x3 + 27a6 + 36x2a4 – 54xa5
= 27x6 – 54ax5+ 117a2x4 – 116a3x3 + 117a4x2 – 54a5x + 27a6
Share your thoughts in the comments
Please Login to comment...