Question 1. Find the values of the following trigonometric ratios:
(i) sin 5π/3
Solution:
We have, sin 5π/3
=sin (2π-π/3) [∵sin(2π-θ)=-sinθ]
=-sin(π/3)
= – √3/2
(ii) sin 17π
Solution:
We have, sin 17π
⇒sin 17π=sin (34×π/2)
Since, 17π lies in the negative x-axis i.e. between 2nd and 3rd quadrant
=sin 17π [∵ sin nπ=0]
= 0
(iii) tan11π/6
Solution:
Clearly, tan(11π/6) = tan ((12π-π)/6)
=tan (4π/2-π/6)
clearly, the angle lies in IV quadrant in which tangent function is negative and the multiple of π/2 is even.
=tan (4π/2-π/6)= -cot (π/6)
=-1/√3
(iv) cos (-25π/4)
Solution:
The cosine function is an even function, Therefore,
cos (-25π/4)=cos (25π/4)
Now, 25π/4=(12×π/2+π/4)
25π/4 lies in the I quadrant and even multiple of π/2
cos (25π/4)=cos (12×π/2+π/4)=cos π/4=1/√2
(v) tan (7π/4)
Solution:
We have, 7π/4=(8π-π)/4 = 2π-π/4
=tan (2π-π/4) [∵ tan(2π-θ)=-tanθ]
=-tan π/4
=-1
(vi) sin 17π/6
Solution:
sin 17π/6= sin (3π-π/6)
=sin (2π+(π-π/6))
=sin (π-π/6) [∵ sin(2π+θ)=sinθ]
=sin π/6 [∵ sin(π-θ)=sinθ]
=1/2
(vii) cos 19π/6
Solution:
cos 19π/6 = cos (3π+(π+π/6))
= cos (2π+(π+π/6))
=cos (π+π/6) [∵ cos(2π+θ)= cosθ)]
=-cos π/6 [∵ cos(π+θ)=-cosθ]
=-√3/2
(viii) sin (-11π/6)
Solution:
sin (-11π/6) = sin (-(2π-π/6))
=sin (2π-π/6) [∵ sin(-θ)= -sinθ]
=-(-sin π/6) [∵ sin(2π-θ)= -sinθ]
=sin π/6
=1/2
(ix) cosec (-20π/3)
Solution:
cosec (-20π/3)= cosec (-(7π-π/3))
= cosec (7π-π/3) [∵ cosec(-θ) = -cosecθ]
= – cosec (2×3π+ (π-π/3))
= – cosec (π-π/3)
= – cosec π/3 [∵ cosec(π-θ)= cosecθ]
= – 2/√3
(x) tan (-13π/4)
Solution:
tan (-13π/4) = -tan (13π/4) [∵ tan(-θ)=-tanθ]
=-tan (3π+π/4)
=- tan (2π+(π+π/4) [∵ tan(2π+θ)=tanθ]
=-tan π/4 [∵ tan(π+θ)=tanθ]
= -1
(xi) cos 19π/4
Solution:
cos 19π/4 = cos (5π-π/4))
= cos (2×2π+(π-π/4)) [∵ cos(2nπ+θ)= cosθ , n ∈ N]
=cos (π-π/4) [∵ cos(π-θ)= -cosθ]
=-cos π/4
=-1/√2
(xii) sin (41π/4)
Solution:
sin (41π/4) = sin (10π+π/4)
=sin (2×5π+π/4) [∵ sin(-θ)= -sinθ]
=sin π/4 [∵ sin(2π-θ)= -sinθ]
=1/√2
(xiii) cos 39π/4
Solution:
cos 39π/4 = cos (10π-π/4))
= cos (2×5π-π/4)
=cos π/4 [∵ cos(2nπ-θ)= cosθ , n ∈ N]
=1/√2
(xiv) sin (151π/6)
Solution:
sin (151π/6) = sin (25π+π/6)
=sin (2×12π+ (π +π/6)) [∵ sin(2nπ+θ)= sinθ , n ∈ N]
=sin (π +π/6) [∵ sin(π+θ)= -sinθ]
=-sin π/6
=-1/2
Question 2. Prove that:
(i) tan 225° cot 405°+tan 765° cot 675°=0
Solution:
Taking LHS
tan 225° cot 405°+tan 765° cot 675°
=tan (π+π/4) cot (2π+π/4)+tan (4π+π/4) cot (4π-π/4)
=tan(π/4)×cot(π/4)+tan(π/4)×{-cot(π/4)} [∵ cot(4π-π/4)=-cot(π/4)]
=1×1+1×(-1)
=0 = RHS (Hence Proved)
(ii) sin (8π/3) cos (23π/6)+cos (13π/3) sin (35π/6)=1/2
Solution:
Taking LHS
sin (8π/3) cos (23π/6)+cos (13π/3) sin (35π/6)
=sin (3π-π/3) cos (4π-π/6)+cos (4π+π/3) sin (6π-π/6)
=sin (π/3) cos (π/6)+cos (π/3) {-sin (π/6)} [∵ sin(6π-θ)= -sinθ]
=√3/2×√3/2+1/2×(-1/2)
=3/4-1/4
=2/4
=1/2= RHS (Hence Proved)
(iii) cos 24° + cos55° + cos125° + cos204° + cos300°=1/2
Solution:
Taking LHS
cos 24° + cos55° + cos125° + cos204° + cos300°
=cos 24° – cos ( π+24°) + cos 55° +cos (π-55°) + cos ( 2π-π/3)
=cos 24° – cos 24° + cos 55° – cos 55° + cos π/3
= cos π/3
= 1/2 = RHS (Hence Proved)
(iv) tan (-225°) cot (-405°)-tan (-765°) cot (675°) = 0
Solution:
Taking LHS
tan (-225°) cot (-405°)-tan (-765°) cot (675°)
=-tan 225° {-cot 405°}+tan 765° cot 675°
=tan (π+π/4) cot (2π+π/4)+tan (4π+π/4) cot (4π-π/4)
=tan(π/4) cot(π/4)+tan(π/4)×{-cot(π/4)} [∵ cot(4π-π/4)=-cot(π/4)]
=1×1+1×(-1)
=1-1
=0 = RHS (Hence Proved)
(v) cos 570° sin 510° + sin (-330°) cos (-390°)=0
Solution:
Taking LHS
cos 570° sin 510° + sin (-330°) cos (-390°)
=cos (3π+π/6) sin (3π-π/6) – sin 330° cos 390° [∵ sin(-θ)= -sinθ and cos(-θ)= cosθ]
=-cos π/6 sin π/6 + sin π/6 cos π/6 [∵ sin(2π-θ)= -sinθ]
=0=RHS (Hence Proved)
(vi) tan (11π/3)- 2sin (4π/6)-3/4cosec2 (π/4)+4cos2 (17π/6)=(3-4√3)/2
Solution:
Taking LHS
tan (4π-π/3)- 2sin (2π/3)-3/4×(√2)2+4cos2 (3π-π/6)
=-tan π/3- 2sin (π-π/3)-3/4×2+4cos2 π/6 [∵ tan(nπ-θ)=-tanθ ∵cos(2nπ-θ)= -cosθ , n ∈ N]
=-√3 – 2sin π/3 -3/2+4×(√3/2)2
=-√3 – 2×(√3/2) -3/2+4×(3/4)
=-√3 – √3 -3/2+3
=-2√3+(-3+6)/2
=-2√3+3/2
=(3-4√3)/2=RHS (Hence Proved)
(vii) 3sin (π/6) sec (π/3)- 4sin (5π/6) cot (π/4)=1
Solution:
Taking LHS
3sin (π/6) sec (π/3)- 4sin (5π/6) cot (π/4)
=3×(1/2)×2- 4sin (π-π/6)×1
=3 – 4sin π/6
=3-4×1/2
=3-2=1=RHS (Hence Proved)
Question 3. Prove that:
(i) 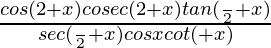
Solution:
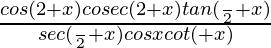 [∵tan(π/2+θ)= -cotθ]
[∵tan(π/2+θ)= -cotθ]
=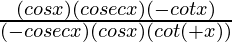 [∵sec(π/2+θ)= -cosecθ]
[∵sec(π/2+θ)= -cosecθ]
=1
=RHS (Hence Proved)
(ii)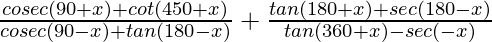 =2
=2
Solution:
Taking LHS
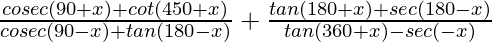
=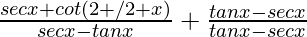 [∵cot(π/2+θ)= -tanθ ∵cot(2π+θ)= cotθ]]
[∵cot(π/2+θ)= -tanθ ∵cot(2π+θ)= cotθ]]
=(sec x+cot(π/2+x))/(secx-tanx)+1
=(sec x-tanx)/(secx-tanx)+1
=1+1
=2=RHS (Hence Proved)
{iii}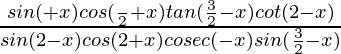 =1
=1
Solution:
Taking LHS
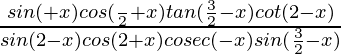 [∵ tan(π/2-θ)= cotθ ∵sin(π/2+θ)= -cosθ]
[∵ tan(π/2-θ)= cotθ ∵sin(π/2+θ)= -cosθ]
=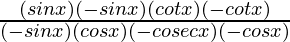 [∵ cotθ= cosθ/sinθ ∵ cosecθ= 1/sinθ]
[∵ cotθ= cosθ/sinθ ∵ cosecθ= 1/sinθ]
=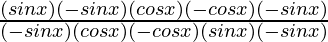
= 1 = RHS (Hence Proved)
(iv) {1+cot x -sec(π/2+x)}{1+cot x + sec(π/2+x)}=2cot x
Solution:
Taking LHS
{1+cot x -sec(π/2+x)}{1+cot x + sec(π/2+x)} [∵ sec(π/2+θ)= -cosecθ]
={1+cot x -(-cosec x)}{1+cot x – cosec x}
={(1+cot x) +cosec x}{(1+cot x) – cosec x}
=(1+cot x)2 -cosec2 x
=1+cot2 x+2cot x -cosec2 x [∵ 1+cot2 θ=cosec2θ]
=cosec2 x+2cot x -cosec2 x
=2cot x=RHS (Hence Proved)
(v) 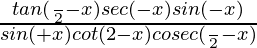 =1
=1
Solution:
Taking LHS
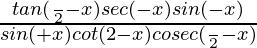
=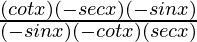
=1=RHS (Hence Proved)
Question 4. Prove that: sin2π/18+sin2π/9+sin27π/18+sin24π/9=2
Solution:
Taking LHS
sin2π/18+sin2π/9+sin27π/18+sin24π/9
=sin2(π/2-4π/9)+sin24π/9+sin2π/9+sin2(π/2-π/9)
=cos24π/9+sin24π/9+sin2π/9+cos2π/9
=1+1=2=RHS (Hence Proved)
Question 5. Prove that: sec(3π/2-x)sec(x-5π/2)+tan(5π/2+x)tan(x-3π/2)=-1
Solution:
Taking LHS:
sec(3π/2-x)sec(x-5π/2)+tan(5π/2+x)tan(x-3π/2)
=sec(3π/2-x)sec(-(5π/2-x))+tan(5π/2+x)tan(-(3π/2-x)) [∵ sec(-θ)= secθ]
=-cosec x sec(5π/2-x)-cot x (-tan(3π/2-x))
=-cosec x cosec x-cot x (-cot x)
=-cosec2 x + cot2 x
=-cosec2 x + cosec2 x – 1 [∵1+cot2 θ=cosec2θ]
=-1=RHS (Hence Proved)
Question 6. In a △ABC, prove that:
(i) cos (A+B) + cos C = 0
Solution:
A+B+C=π
A+B=π-C ———-(1)
Taking LHS
cos (A+B) + cos C
Putting the value of A+B
cos (π-C) + cos C [∵ cos(π-θ)= -cosθ]
=-cos C + cos C
=0 = RHS (Hence Proved)
(ii) cos (A+B)/2=sin C/2
Solution:
Taking LHS
cos (A+B)/2
Putting the value of A+B from (1)
=cos (π-C)/2
=cos (π/2-C/2) [∵ cos(π/2+θ)= sinθ]
=sin C/2 = RHS (Hence Proved)
(iii) tan (A+B)/2=cot C/2
Solution:
Taking LHS
tan (A+B)/2
Putting the value of A+B from (1)
=tan(π-C)/2
=tan (π/2-C/2) [∵ tan(π/2-θ)= cotθ]
=cot C/2 = RHS (Hence Proved)
Question 7. If A,B,C,D be the angles of a cyclic quadrilateral, taken in order, prove that
cos(180°-A)+cos(180°+B)+cos(180°+C)-sin(90°+D)=0
Solution:
Since, A, B, C, D are the angles of a cyclic quadrilateral
Therefore, A+B+C+D=2π
or A+B=π or C+D=π
A=π-B also C=π-D
Taking LHS
cos(180°-A)+cos(180°+B)+cos(180°+C)-sin(90°+D)
=cos(π-(π-B))+cos(π+B)+cos(π+(π-D))-sin(π/2+D) [∵ cos(π+θ)= -cosθ]
=cos B +(-cos B) +cos D -cos D
=cos B – cos B +0
=0 =RHS (Hence Proved)
Question 8. Find x from the following equations
(i) cosec (π/2+θ) + x cos θ cot(π/2+θ)=sin(π/2+θ)
Solution:
We have,
cosec (π/2+θ) + x cos θ cot(π/2+θ)=sin(π/2+θ)
⇒ sec θ + x cos θ (-tanθ)=cos θ
⇒1/cosθ – x cos θ (sinθ/cosθ)=cos θ
⇒1/cosθ – x sinθ=cos θ
⇒1-x sinθcosθ/cosθ =cos θ
⇒1-x sinθcosθ =cos2 θ
⇒1-cos2θ =x sinθcosθ
⇒sin2θ =x sinθcosθ
⇒x=sinθ/cosθ
⇒x=tanθ
(ii) x cot (π/2+θ) + tan (π/2+θ)sin θ+ cosec(π/2+θ)=0
Solution:
We have,
x cot (π/2+θ) + tan (π/2+θ)sin θ+ cosec(π/2+θ)=0
⇒-x tan θ – cot θ sin θ+ sec θ=0
⇒-x sin θ/cos θ – (cos θ/sin θ) sin θ+ 1/cos θ=0
⇒-x sin θ/cos θ – cos θ + 1/cos θ=0
⇒(-x sin θ – cos2θ + 1)/cos θ=0
⇒-x sin θ +1- cos2θ =0
⇒-x sin θ + sin2θ =0
⇒x sin θ = sin2θ =0
⇒x = sin θ
Question 9. Prove that:
(i) tan 4π – cos (3π/2)-sin (5π/6)cos (2π/3)=1/4
Solution:
Taking LHS
tan 4π – cos (3π/2)-sin (5π/6)cos (2π/3) [∵ tan nπ= 0, ∀ n∈ Z ]
=0- cos (π+π/2)-sin (π-π/6)cos(π/2-π/6)
=0- (cos π/2)- (sin π/6)(-sin π/6)
=0-0+sin2 π/6
=(1/2)2
=1/4=RHS (Hence Proved)
(ii) sin (13π/3) sin (8π/3) + cos (2π/3)sin (5π/6)=1/2
Solution:
Taking LHS
sin (13π/3) sin (8π/3) + cos (2π/3)sin (5π/6)
=sin (4π+π/3) sin (3π-π/3) + cos (π/2+π/6)sin (π-π/6) [∵ sin (4π+θ)= sinθ & sin (3π-θ)= sinθ]
=sin π/3 sin π/3 + (-sin π/6) sin π/6
=(√3/2)×(√3/2)-(1/2)×(1/2)
=3/4-1/4
=2/4=1/2=RHS (Hence Proved)
(iii) sin (13π/3) sin (2π/3) + cos (4π/3)sin (13π/6)=1/2
Solution:
Taking LHS
sin (13π/3) sin (2π/3) + cos (4π/3)sin (13π/6)
=sin (4π+π/3) sin (π/2-π/6) + cos (π+π/6)sin (2π+π/6)
=sin π/3 cos π/6 – cos π/3 sin π/6
=(√3/2)×(√3/2)-(1/2)×(1/2)
=3/4-1/4
=2/4=1/2=RHS (Hence Proved)
(iv) sin (10π/3) cos (13π/6) + cos (8π/3)sin (5π/6)=-1
Solution:
Taking LHS
sin (10π/3) cos (13π/6) + cos (8π/3)sin (5π/6)
=sin (3π+π/3) cos (2π+π/6) + cos (3π-π/3)sin (π-π/6)
=-sin (π/3) cos (π/6) + cos π/3 (- sin π/6) [∵ sin (3π+θ)= -sinθ & cos (3π-θ)= -cosθ]
=(-√3/2)×(-√3/2)-(1/2)×(1/2)
=-3/4-1/4
=-4/4=-1=RHS (Hence Proved)
(V) tan (5π/4) cot (9π/4) + tan (17π/4) cot (15π/4)=0
Solution:
Taking LHS
tan (5π/4) cot (9π/4) + tan (17π/4) cot (15π/4)
=tan (π+π/4) cot (2π+π/4) + tan (4π+π/4) cot (4π-π/4)
=(tan π/4) (cot π/4) + (tan π/4) (-cot π/4)
=1.1+1.(-1)
=1-1=0 RHS (Hence Proved)
Share your thoughts in the comments
Please Login to comment...