Every mathematical function, from the simplest to the most complex, has an inverse. In mathematics, inverse usually means the opposite. In addition, the inverse is subtraction. For multiplication, it’s division. In the same way for trigonometric functions, it’s the inverse trigonometric functions. Trigonometric functions are the functions of an angle. The term function is used to describe the relationship between two sets of numbers or variables. In modern mathematics, there are six basic trigonometric functions: sine, cosine, tangent, secant, cosecant, and cotangent. The inverse of these functions is inverse sine, inverse cosine, inverse tangent, inverse secant, inverse cosecant, and inverse cotangent. Trigonometric functions are many to one function but we know that the inverse of a function exists if the function is bijective (one-one onto). So, if we restrict the domain of trigonometric functions, then these functions become bijective and the inverse of trigonometric functions are defined within the restricted domain.
Note: Inverse of f is denoted by ” f -1 “.
Domain and Range of Inverse Trigonometric Functions
The elements of X are called the domain of f and the elements of Y are called the domain of f. The images of the element of X is called the range of which is a subset of Y. The below image demonstrates the domain, codomain, and range of the function.

Below is The Table for Domain and Range of Inverse Trigonometric Functions:
Function
| Domain
| Range
|
|---|
| sin-1x | [-1, 1] | [ -pi/2, pi/2 ] |
| cos-1x | [-1, 1] | [0, pi] |
| tan-1x | R | [-pi/2, pi/2] |
| cot-1x | R | (0, pi) |
| sec-1x | R-(-1,1) | [0, pi], {pi/2} |
| cosec-1x | R-(-1,1) | [ -pi/2, pi/2 ] – {0} |
Derivatives of Inverse Trigonometric Functions using the First Principle
Let’s understand this topic by taking some problems, which we will solve by using the First Principal.
Problem Statement: sin-1x = y, under given conditions -1 ≤ x ≤ 1, -pi/2 ≤ y ≤ pi/2. Solve this problem by using the First Principal.
Solution:
Firstly taking sin on both sides, hence we get x = siny this equation is nothing but a function of y. Instead of finding dy/dx we will find dx/dy, so by definition of derivative we can write ((f(y + h) – f(y))/h), where h -> 0 under the limiting condition (see fourth line). Now replace the function with ((sin(y + h) – siny)/h) where h -> 0 under the limiting condition. Using the identity we can solve further. As we see in the last line of the below solution that siny and cosy are not dependent on the limit h -> 0 that’s why we had taken them out.
sin(sin x) = sin y
x = sin y
By definition of derivative,
dx/dy = limh->0 {f(y + h) – f(y)} / h
= limh->0 { sin(y + h) – siny } / h
Using identity: sin(A + B) = sinA.cosB + cosA.sinB, we can write,
= limh->0 (sin y . cos h + cos y . sin h – sin y) / h
= limh->0 (sin y . cos h – sin y + cos y . sin h) / h
= limh->0 {sin y(cos h – 1) / h} + {cos y . sin h) / h}
= sin y. limh->0 {(cos h – 1) / h} + cos y. limh->0 {sin h / h}
Now, we had taken -1 common from the expression (cos h-1) and we get (see in 1st line of below figure). Now using the formula as written in line 2 of the below figure we can write our expression dx/dy = cos y, if we reciprocal this term we get dy/dx = 1/cos y this. We know that sin2 x + cos2 x = 1, by simplifying this formula to get our answer, we simplified it till the 6th line of the below figure.
But how had we written the final answer to this problem?
Since -pi/2 ≤ sin-1x ≤ pi/2. Hence -pi/2 ≤ y ≤ pi/2, we had written y in place of sin-1x, look at above figure second line we had written x = siny, if we write this for y we can write this like y = sin-1x this, that’s why we had written y in place of sin-1x. This implies 0 ≤ cosy ≤ 1 because y is an angle which lies first and fourth quadrant only, but one thing to note here, since cosy is in the denominator of dy/dx hence it cannot be zero,
Now we remove the equality 0 < cos y ≤ 1 by this inequality we can clearly say that cosy is a positive property, hence we can remove -ve sign from the second last line of the below figure. So, this implies dy/dx = 1 over the quantity square root of (1 – x2), which is our required answer.
Note: In the solution after removing square we are getting square-root on another side and with square-root +ve and – ve both signs take place which is denoted by +-squareroot in the solution.
= sin y. limh->0 { (cos h – 1) / h } + cos y. limh->0 { sin h / h }
By using the formula: limh->0 (1 – cos h) / h = 0 and limh->0 sin h / h = 1, we can write,
dx / dy = cos y
dy / dx = 1 / cos y …..(1)
We know that sin2y + cos2y = 1, so cos2y = 1 – sin2y
⇒ cos = +- √(1 – sin2y), taking siny = x
we get, cosy = +-√(1 – x2)
dy / dx = 1 / √(1 – x2)
If we draw the graph of sin inverse x, then the graph looks like this:

Examples
Example 1: Differentiate the function f(x) = cos-1x Using First Principle.
Solution:
For solving and finding the cos-1x ,we have to remember below three listed formulae.
- limh->0 {f(x + h) – f(x)} / h
- cos-1x + sin-1x = pi/2
- cos-1x = pi/2 – sin-1x
Now, let’s solve, we have.
f(x) = cos-1x
f(x + h) = cos-1(x + h)
limh->0 {cos-1(x + h ) – cos-1(x)} / h
limh->0 {pi/2 – sin-1(x + h) – (pi/2 – sin-1x) } / h
limh->0 {pi/2 – sin-1(x + h) – pi/2 + sin-1x } / h
Taking – sign common, we get
– limh->0 {sin-1(x + h) – sin-1x} / h
Since we know that limh->0 { sin-1(x + h) – sin-1x } / h = 1 / √(1 – x2)
Putting the value in our solution we get,
– 1 / √(1 – x2)
If we draw the graph of cos inverse x, then the graph looks like this.

Example 2: Solve f(x) = tan-1(x) Using first Principle.
Solution:
For solving and finding tan-1x, we have to remember some formulae, listed below.
- limh->0 {f(x + h) – f(x)} / h
- tan-1(θ/θ) = 1
- tan-1x – tan-1y = tan-1[(x – y) / (1 + xy)]
f(x) = tan-1x
f(x + h) = tan-1(x + h)
Apply 1st formula
limh->0 {tan-1(x + h) – tan-1x } / h
Now Apply 3rd formula
limh->0 tan-1[(x – h – x) / (1 + (x + h)x] / h
limh->0 tan-1[(h / (1 + x2 + xh ] / h . [(1 + x2 + xh) / (1 + x2 + xh)]
limh->0 tan-1 {h / 1 + x2 + xh} / {h / 1 + x2 + xh} . limh->0 1 / 1 + x2 + xh
Now we made the solution like so that we apply the 2nd formula
= 1 . 1 / (1 + x2 + x . 0)
= 1 / (1 + x2)
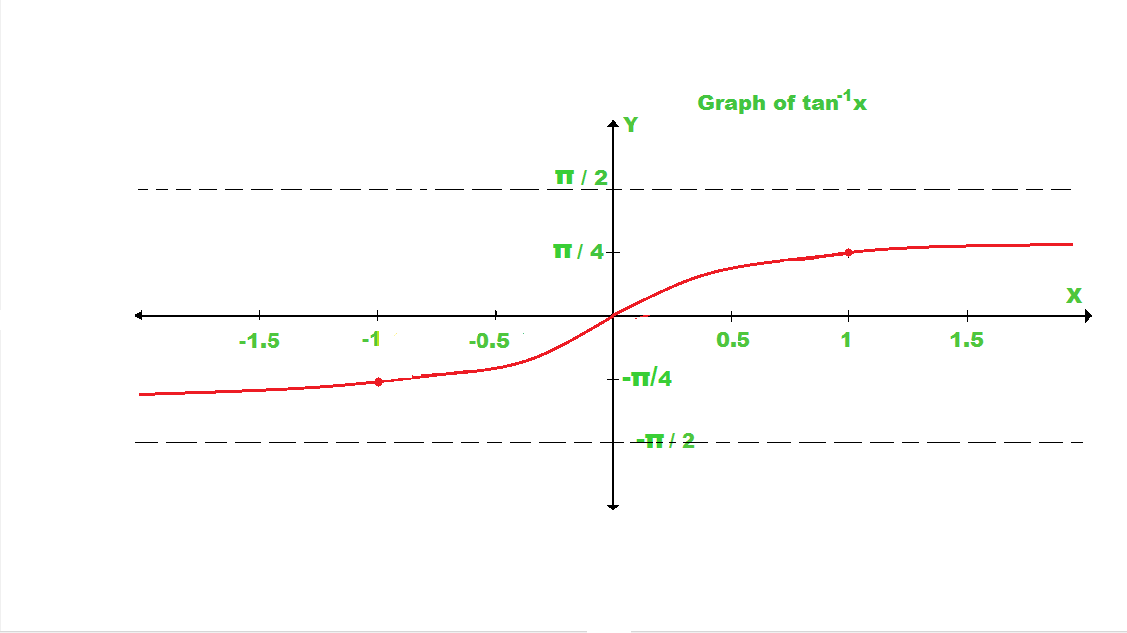
If we draw the graph of tan inverse x, then the graph looks like this.
The Derivative of Inverse Trigonometric Functions using Chain Rule
Before using the chain rule, we have to know first that what is chain rule?
uv = u’v + uv’
The above expression demonstrated the chain rule, where u is the 1st function and v is the 2nd function and to apply the chain rule we have to first take the derivative of u and multiply with v on the other segment we have to take the derivative of v and multiply it with u and then add both of them. We use this chain rule to find the derivative of the Inverse Trigonometric Function.
Formulae of Inverse Trigonometric Functions
In the below figure there is the list of formulae of Inverse Trigonometric Functions which we will use to solve the problems while solving Derivative of Inverse Trigonometric Functions.

Examples
Let’s take some of the problems based on the chain rule to understand this concept properly.
Note: In the all below Solutions y’ means dy/dx
Problem 1: y = tan-1(1/x)
Solution :
We have to find out the derivative of the above question, so first, we have to substitute the formulae of tan-1x as we discuss in the above list (line 3). Then, we have to apply the chain rule. Then put the value of x in that formulae which are (1/x) then by applying the chain rule we have solved the question by taking there derivatives.
By using chain rule,
y’ = (tan-1x)’
= {1/1 + (1/x2) } . (-1/x2)
= – x2 / (x2 + 1) . x2
Problem 2: y = sin-1(1 – x)
Solution:
We have to find out the derivative of the above question, so first, we have to substitute the formulae of tan-1x as we discuss in the above list (line 1). Then, we have to apply the chain rule. Then put the value of x in that formulae which are (1 – x) then by applying the chain rule, we have solved the question by taking their derivatives.
By using chain rule,
y’ = (sin-1(1 – x))’
= 1 / 1 – (x – 1)2
= 1 / √(1 – (x2 – 2x + 1))
= 1 / √(2x – x2)
Problem 3: y = (1/a) tan-1(x/a)
Solution:
As we had solved the first problem in the same way we are going to solve this problem too, we have to find out the derivative of the above question, so first, we have to substitute the formulae of tan-1x as we discuss in the above list (line 3). Then apply the chain rule. As we see 1/a is constant, so we take it out and applying the chain rule in tan-1(x/a). Solved it by taking the derivative after applying chain rule.
By using chain rule,
y’ = ((1 / a) tan-1(x / a))’
= (1 / a) {1 / (1 + (x / a))} . (x / a)’
= 1 / a . {1 / (1+ (x2 / a2))} . (1 / a)
= 1 / a2 . {a / (a2 + x2)}
= a / a2 + x2
Problem 4: y = cot-1(1/x2)
Solution:
As we are solving the above three problem in the same way this problem will solve
By using chain rule,
y’ = (cot-1(1 / x2))’
= { – 1 / (1 + (1 / x2))2 } . (1 / x2)’
= { – 1 / (1 + (1 / x4)) . (-2x-3)
= 2x4 / (x4 + 1)x3
= 2x / (1 + x4)
We have to find out the derivative of cot-1(1/x2), so as we are following first we have to substitute the formulae of cot-1x in the above list of Trigonometric Formulae (line 4). Then apply the chain rule and find the derivative of the problem and after solving, we get our required answer.
The Derivative of Inverse Trigonometric Function as Implicit Function
Firstly we have to know about the Implicit function. What are Implicit functions? Let’s take one function for example, y = 2x + 3. So in this function variable y is dependent on variable x, which means when the value of x change in the function value of y will also change. So this type of function in which dependent variable (y) is isolated means, comes alone in one side(left-hand side) these functions are not implicit functions they are Explicit functions.
Let’s take another example, x + sin xy -y = 0. As we see in this function we cannot separate any one variable alone on one side, which means we cannot isolate any variable, because we have both of the variables x and y as the angle of sin. So, this type of function in which we cannot isolate the variable. This type of function is known as Implicit functions. Let’s take the problem and we solve that problem by using implicit differentiation.
Example: y = cos-1x
Solution:
For finding derivative of Inverse Trigonometric Function using Implicit differentiation. To start solving firstly we have to take the derivative x in both the sides, the derivative of cos(y) w.r.t x is -sin(y)y’. The reciprocal of sin is cosec so we can write in place of -1/sin(y) is -cosec(y) (see at line 7 in the below figure). Now we have to write the answer in terms of x, from equation(1) we draw the triangle for cos(y) = x and find the perpendicular of the triangle. Now the formula of cosec is hyp/perpendicular, now with the help of the triangle that we had drawn, we can find the cosec(y) by putting it in the formula. Then put the value of cosec(y) in the eq(2). We get our required answer(see the last line).
y = cos-1x
y’ = (cos x)’
we can write,
cos y = x …(1)
d/dx (cos y) = d/dx (x)
(-sin y) y’ = 1 / siny
y’ = -cosec y …(2)

from eq (1), formula of cos(x) = base / hyp , we can find the perpendicular of triangle
perpendicular = √(1 – x2)
formula of cosec(x) = hyp / perpendicular, which is,
= 1 / √(1 – x2)
Putting the value of cosec in eq(2), we get
y’ = -1 / √(1 – x2)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...