Class 11 RD Sharma solutions – Chapter 29 Limits – Exercise 29.7 | Set 2
Last Updated :
30 Apr, 2021
Question 32. limx→0[{sin(a + x) + sin(a – x) – 2sina}/(xsinx)]
Solution:
We have,
limx→0[{sin(a + x) + sin(a – x) – 2sina}/(xsinx)]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{2sin(\frac{a+x+a-x}{2})sin(\frac{a+x-a+x}{2})}{xsinx}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-66360dd57fccc134f7db555909bc2ae0_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{2sina(cosx-1)}{xsinx}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-811064e29166c16eabc4b377b2ad9629_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{-2sina(1-cosx)}{xsinx}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c1c77170e0238bd3fd3ae9ee89f82ed3_l3.png)
= ![Rendered by QuickLaTeX.com -2sina\lim_{x\to0}[\frac{2sin^2\frac{x}{2}}{x.2sin\frac{x}{2}cos\frac{x}{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-68850d6f29fc8a5670ed4abd65066897_l3.png)
= ![Rendered by QuickLaTeX.com -2sina\lim_{x\to0}[\frac{sin\frac{x}{2}}{x.cos\frac{x}{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6769142d3ee228885787f37bed3d574b_l3.png)
= ![Rendered by QuickLaTeX.com -2sina\lim_{x\to0}[\frac{tan\frac{x}{2}}{x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-16ec4ef82f9bb1a2a713300b45ffb18a_l3.png)
= ![Rendered by QuickLaTeX.com -2sina\lim_{x\to0}[\frac{tan\frac{x}{2}}{\frac{x}{2}×2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-73998cb37e7e2b08d4ab83e6772d1867_l3.png)
= -2sina × (1/2)
= -sina
Question 33. limx→0[{x2 – tan2x}/(tanx)]
Solution:
We have,
limx→0[{x2-tan2x}/(tanx)]
Dividing numerator by 2x and denominator by x.
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{(\frac{x^2}{2x}-\frac{tan2x}{2x})×2x}{\frac{tanx}{x}×x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-feec0b12e55c016f75d8de538b2e3056_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{2(\frac{x}{2}-\frac{tan2x}{2x})}{\frac{tanx}{x}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ed3433e91e1537bade7c0fd0e8095f4a_l3.png)
= 2(0 – 1)/1
= -2
Question 34. limx→0[{√2 – √(1 + cosx)}/x2]
Solution:
We have,
limx→0[{√2 – √(1 + cosx)}/x2]
On rationalizing numerator
= limx→0[{2-(1+cosx)}/x2{√2+√(1+cosx)}]
= limx→0[(1-cosx))/x2{√2+√(1+cosx)}]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{sin^2(\frac{x}{2})}{x^2.(\sqrt{2}+\sqrt{1+cosx}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2a4e5f3f9d0f20789550851dba52bb1f_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{2sin^2(\frac{x}{2})}{(\frac{x}{2})^2×4}×\frac{1}{(\sqrt{2}+\sqrt{1+cosx}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7a913792b31092d08066d979a6659229_l3.png)
= 2 × (1/4) × [1/{√2 + √(1 + 1)}]
= (2/4) × (1/2√2)
= (1/4√2)
Question 35. limx→0[{xtanx}/(1 – cosx)]
Solution:
We have,
limx→0[{xtanx}/(1 – cosx)]
On dividing the numerator and denominator by x2
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{\frac{tanx}{x}}{\frac{2sin^2(\frac{x}{2})}{x^2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d69a6652568bcc4505ee2da4dae1c58d_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{\frac{tanx}{x}}{\frac{2sin^2(\frac{x}{2})}{(\frac{x}{2})^2×4}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-90772350a1de4a6d3769cf8eddeb93d2_l3.png)
As we know that limx→0[sinx/x] = 1 and limx→0[tanx/x] = 1
= (4/2)
= 2
Question 36. limx→0[{x2 + 1 – cosx}/(xsinx)]
Solution:
We have,
limx→0[{x2 + 1 – cosx}/(xsinx)]
= limx→0[{x2 + 2sin2(x/2)}/(xsinx)]
On dividing the numerator and denominator by x2
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{1+\frac{2sin^2\frac{x}{2}}{x^2}}{{\frac{sinx}{x}}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-28c10a1939d6964e5e3d872e5b87628c_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{1+2(\frac{sin\frac{x}{2}}{\frac{x}{2}×2})^2}{{\frac{sinx}{x}}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-99ba7fcafce77baa425386289e15db32_l3.png)
As we know that limx→0[sinx/x] = 1
= 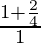
= 3/2
Question 37. limx→0[sin2x{cos3x – cosx}/(x3)]
Solution:
We have,
limx→0[sin2x{cos3x – cosx}/(x3)]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}\frac{(sin2x)×[-2sin(\frac{3x+x}{2})sin(\frac{3x-x}{2})]}{x^3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-85e8e0874f36c3d5ec35f266af781b63_l3.png)
= 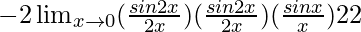
As we know that limx→0[sinx/x] = 1
= -2 × 2 × 2
= -8
Question 38. limx→0[{2sinx° – sin2x°}/(x3)]
Solution:
We have,
limx→0[{2sinx°-sin2x°}/(x3)]
= limx→0[{2sinx°-2sinx°cosx°}/(x3)]
= limx→0[2sinx°{1-cosx°}/(x3)]
= limx→0[2sinx°{2sin2(x°/2)}/(x3)]
= 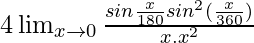
= 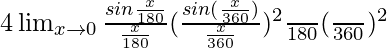
= 4 × [π3/(180 × 360 × 360)]
= (π/180)3
Question 39. limx→0[{x3.cotx}/(1 – cosx)]
Solution:
We have,
limx→0[{x3.cotx}/(1 – cosx)]
= limx→0[x3/{tanx(1 – cosx)}]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{x}{tanx}×\frac{x^2}{2sin^2\frac{x}{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-05e26a851561f165216de832fcfb9e68_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{x}{tanx}×\frac{\frac{x^2}{4}×4}{2sin^2\frac{x}{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a13a7e91af5c85a1966649f6dbfaa290_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{x}{tanx}×(\frac{\frac{x}{2}}{sin\frac{x}{2}})^2×2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7a6644fe7f80aff73a5caeca2af863a4_l3.png)
As we know that limx→0[sinx/x] = 1 and limx→0[tanx/x] = 1
= 2
Question 40. limx→0[{x.tanx}/(1 – cos2x)]
Solution:
We have,
limx→0[{x.tanx}/(1 – cos2x)]
= limx→0[{x.tanx}/(2sin2x)]
On dividing the numerator and denominator by x2
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{\frac{tanx}{x}}{2\frac{sin^2x}{x^2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-db6a69f080eeb741b301c14a025401f1_l3.png)
As we know that limx→0[sinx/x] = 1 and limx→0[tanx/x] = 1
= (1/2)
Question 41. limx→0[{sin(3 + x) – sin(3 – x)}/x]
Solution:
We have,
limx→0[{sin(3 + x) – sin(3 – x)}/x]
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{2cos(\frac{3+x+3-x}{2})sin(\frac{3+x-3+x}{2})}{x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-24329b04c37e4dd2bc1e59c7632c49d4_l3.png)
= 2Limx→0[cos3.sinx/x]
= 2cos × 3limx→0[sinx/x]
As we know that limx→0[sinx/x] = 1
= 2cos3
Question 42. limx→0[{cos2x – 1)}/(cosx – 1)]
Solution:
We have,
limx→0[{cos2x – 1)}/(cosx – 1)]
= limx→0[(2sin2x)/{2sin2(x/2)}]
= limx→0[(sin2x)/{sin2(x/2)}]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{sin^2x}{x^2}×x^2][\frac{1}{\frac{sin^2\frac{x}{2}}{(\frac{x}{2})^2}×(\frac{x}{2})^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8ac47d987366da3df9ec4052f874ced9_l3.png)
As we know that limx→0[sinx/x] = 1
= (x2) × (4/x2)
= 4
Question 43. limx→0[{3sin2x – 2sinx2)}/(3x2)]
Solution:
We have,
limx→0[{3sin2x – 2sinx2)}/(3x2)]
= limx→0[(3sin2x/3x2) – (2sinx2/3x2)]
As we know that limx→0[sinx/x] = 1
= 1 – 2/3
= (3 – 2)/3
= (1/3)
Question 44. limx→0[{√(1 + sinx) – √(1 – sinx)}/x]
Solution:
We have,
limx→0[{√(1 + sinx) – √(1 – sinx)}/x]
On rationalizing numerator.
= limx→0[{(1 + sinx) – (1 – sinx)}/x{√(1 + sinx) + √(1 – sinx)}]
= limx→0[2(sinx)/x{√(1 + sinx) + √(1 – sinx)}]
= ![Rendered by QuickLaTeX.com 2\lim_{x\to0}[\frac{sinx}{x}×\frac{1}{\sqrt{1+sinx}+\sqrt{1-sinx}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-87bd533ec94d2419c0cbf010335f96f3_l3.png)
As we know that limx→0[sinx/x] = 1
= 2 × {1/(√1 + √1)}
= 2/2
= 1
Question 45. limx→0[(1 – cos4x)/x2]
Solution:
We have,
limx→0[(1 – cos4x)/x2]
= limx→0[2sin22x/x2]
= ![Rendered by QuickLaTeX.com 2\lim_{x\to0}[(\frac{sin2x}{2x})^2×4]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b09f77b6ed559568789d03494a892d99_l3.png)
As we know that limx→0[sinx/x] = 1
= 2 × 4
= 8
Question 46. limx→0[(xcosx + sinx)/(x2 + tanx)]
Solution:
We have,
limx→0[(xcosx + sinx)/(x2 + tanx)]
= limx→0[x(cosx+sinx/x)/x(x + tanx/x)]
= limx→0[(cosx + sinx/x)/(x + tanx/x)]
= 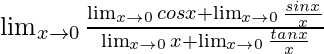
As we know that limx→0[tanx/x] = 1
= (1 + 1)/(1 + 0)
= 2
Question 47. limx→0[(1 – cos2x)/(3tan2x)]
Solution:
We have,
limx→0[(1 – cos2x)/(3tan2x)]
= limx→0[2sin2x/3tan2x]
=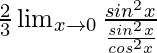
= (2/3)limx→0[cos2x]
= (2/3)
Question 48. limθ→0[(1 – cos4θ)/(1 – cos6θ)]
Solution:
We have,
limθ→0[(1 – cos4θ)/(1 – cos6θ)]
= limθ→0[2sin22θ/2sin23θ]
= limθ→0[sin22θ/sin23θ]
=![Rendered by QuickLaTeX.com \lim_{θ\to0}[\frac{sin^22θ}{(2θ)^2}×(2θ)^2×\frac{1}{\frac{sin^23θ}{(3θ)^2}×(3θ)^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4dec7e2b5f380bccbbdf500d850222aa_l3.png)
= [(4θ2)/(9θ2)]
= (4/9)
Question 49. limx→0[(ax + xcosx)/(bsinx)]
Solution:
We have,
limx→0[(ax + xcosx)/(bsinx)]
On dividing the numerator and denominator by x
= 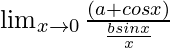
As we know that limx→0[sinx/x] = 1
=(a + cos 0)/b × 1
= (a + 1)/b
Question 50. limθ→0[(sin4θ)/(tan3θ)]
Solution:
We have,
limθ→0[(sin4θ)/(tan3θ)]
=![Rendered by QuickLaTeX.com \lim_{θ\to0}[\frac{sin4θ}{(4θ)}×(4θ)×\frac{1}{\frac{tan3θ}{(3θ)}×(3θ)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-865f6b1094662c817f85314c19ca739b_l3.png)
As we know that limx→0[sinx/x] = 1 and limx→0[tanx/x] = 1
= (4θ/3θ)
= (4/3)
Question 51. limx→0[{2sinx – sin2x}/(x3)]
Solution:
We have,
limx→0[{2sinx – sin2x}/(x3)]
= limx→0[{2sinx – 2sinxcosx}/(x3)]
= limx→0[2sinx{1 – cosx}/(x3)]
= limx→0[2sinx{2sin2(x/2)}/(x3)]
= 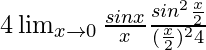
As we know that limx→0[sinx/x] = 1
= (4/4)
= 1
Question 52. limx→0[{1 – cos5x}/{1 – cos6x}]
Solution:
We have,
limx→0[{1 – cos5x}/{1 – cos6x}]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{2sin^2(\frac{5x}{x})}{2sin^23x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6d5aff3445401d43fed09bad1312f3cd_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{sin^2(\frac{5x}{2})}{(\frac{5x}{2})^2}×\frac{25x^2}{4}×\frac{1}{\frac{sin^23x}{(3x)^2}×9x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e87da3a7df2689761c19f3baca8e6bd5_l3.png)
As we know that limx→0[sinx/x] = 1
= 25/(4 × 9)
= (25/36)
Question 53. limx→0[(cosecx – cotx)/x]
Solution:
We have,
limx→0[(cosecx – cotx)/x]
= limx→0[(1/sinx – cosx/sinx)/x]
= limx→0[(1 – cosx)/x.sinx]
= limx→0[2sin2(x/2)/x.sinx]
= ![Rendered by QuickLaTeX.com 2\lim_{x\to0}[\frac{sin^2(\frac{x}{2})}{(\frac{x}{2})^2}×(\frac{x^2}{4})×\frac{1}{\frac{xsinx}{x^2}×x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-648f30f757ea89bba3dd4896b8aecf96_l3.png)
As we know that limx→0[sinx/x] = 1
= 2/4
= 1/2
Question 54. limx→0[(sin3x + 7x)/(4x + sin2x)]
Solution:
We have,
limx→0[(sin3x + 7x)/(4x + sin2x)]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{\frac{sin3x}{3x}×3x+7x}{\frac{sin2x}{2x}×2x+4x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2165943c344b9c2db843c57dfcacc1af_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{x(\frac{sin3x}{3x}×3+7)}{x(\frac{sin2x}{2x}×2+4)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0ea624fa248d05e2fdd54f019c111d04_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{(\frac{sin3x}{3x}×3+7)}{(\frac{sin2x}{2x}×2+4)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-40e2ba8600df639ee40959c1c495ccd1_l3.png)
As we know that limx→0[sinx/x] = 1
= (7 + 3)/(4 + 2)
= 10/6
= 5/3
Question 55. limx→0[(5x + 4sin3x)/(4sin2x + 7x)]
Solution:
We have,
limx→0[(5x + 4sin3x)/(4sin2x + 7x)]
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{5x+4\frac{sin3x}{3x}×3x}{4\frac{sin2x}{2x}×2x+7x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2a9dd8f7db8ab4ceb1c7802742908ad0_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{x(5+4\frac{sin3x}{3x}×3)}{x(4\frac{sin2x}{2x}×2+7)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-63ff2fc663db111334c67c3b4a05a99f_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{(5+4\frac{sin3x}{3x}×3)}{(4\frac{sin2x}{2x}×2+7)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-447169ec304440083063e51d5872d06e_l3.png)
As we know that limx→0[sinx/x] = 1
= (5 + 4 × 3)/(4 × 2 + 7)
= (17/15)
Question 56. limx→0[(3sinx – sin3x)/x3]
Solution:
We have,
limx→0[(3sinx – sin3x)/x3]
= limx→0[{3sinx – (3sinx – 4sin3x)/x3]
= limx→0[(4sin3x)/x3]
= 4Limx→0[{(sinx)/x}3]
As we know that limx→0[sinx/x] = 1
= 4 × 1
= 4
Question 57. limx→0[(tan2x – sin2x)/x3]
Solution:
We have,
limx→0[(tan2x – sin2x)/x3]
= limx→0[(sin2x/cos2x-sin2x)/x3]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{sin2x(\frac{1}{cos2x}-1)}{x^3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3d60e7cdb03a70b99e5a8520989d339a_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{sin2x(1-cos2x)}{cos2x.x^3}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bc0c3f0c1a147400b4f582c987103384_l3.png)
= limx→0[(2sin2x.sin2x)/(x3cos2x)]
= ![Rendered by QuickLaTeX.com 2\lim_{x\to0}[\frac{sin2x}{2x}×2×(\frac{sinx}{x})^2×\frac{1}{cos2x}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-86ccb78b10b0e55f47aec169b702d416_l3.png)
As we know that limx→0[sinx/x] = 1
= 2 × 2/cos0
= 4
Question 58. limx→0[(sinax + bx)/(ax + sinbx)]
Solution:
We have,
limx→0[(sinax + bx)/(ax + sinbx)]
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{\frac{sinax}{ax}×ax+bx}{ax+\frac{sinbx}{bx}×bx}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ba6be2a818a21aca0d5d421e3ddeadf1_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{x(\frac{sinax}{ax}×x+b)}{x(a+\frac{sinbx}{bx}×b)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2b94c5cf45dbe25c22be46c6b3637fb3_l3.png)
= ![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{(\frac{sinax}{ax}×x+b)}{(a+\frac{sinbx}{bx}×b)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c8b64481d1750cef76ceb5febd2b1cc4_l3.png)
As we know that limx→0[sinx/x] = 1
= (1 × a + b)/(a + 1 × b)
= (a + b)/(a + b)
= 1
Question 59. limx→0[cosecx-cotx]
Solution:
We have,
limx→0[cosecx – cotx]
= limx→0[1/sinx – cosx/sinx]
= limx→0[(1 – cosx)/sinx]
= limx→0[{2sin2(x/2)}/{2sin(x/2)cos(x/2)}]
= limx→0[sin(x/2)/cos(x/2)]
= limx→0[tan(x/2)/ x/2] × x/2
As we know that limx→0[tanx/x] = 1
= 0
Question 60. limx→0[{sin(α + β)x + sin(α – β)x + sin2αx}/{cos2βx – cos2αx}]
Solution:
We have,
limx→0[{sin(α + β)x + sin(α – β)x + sin2αx}/{cos2βx – cos2αx}]
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{2sin(\frac{αx+βx+αx-βx}{2})cos(\frac{αx+βx-αx+βx}{2})+2sinαx.cosαx}{(1-sin^2βx)-(1-sin^2αx)}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-141a64da0bc5523c29a0b4f983f45f3d_l3.png)
= limx→0[{2sinαx.cosβx + 2sinαx.cosαx}/(sin2αx – sin2βx)]
= limx→0[{2sinαx(cosβx + cosαx)}/(sin2αx – sin2βx)]
= ![Rendered by QuickLaTeX.com 2\lim_{x\to0}[\frac{\frac{sinαx}{αx}×αx×(cosβx+cosαx)}{\frac{sin^2αx}{α^2x^2}×α^2x^2-\frac{sin^2βx}{β^2x^2}×β^2x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-253d4549ce05f40c7298f44a7825632d_l3.png)
= 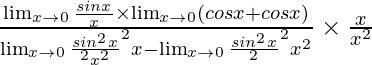
As we know that limx→0[sinx/x] = 1
= [{2 × α × 1 × (1 + 1)}/(α2 – β2)] × (1/0)
= (1/0)
= ∞
Question 61. limx→0[(cosax – cosbx)/(cosecx – 1)]
Solution:
We have,
limx→0[(cosax – cosbx)/(cosecx – 1)]
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{-2sin(\frac{ax+bx}{2})sin(\frac{ax-bx}{2})}{-2sin^2(\frac{cx}{2})}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5ec7061404257761b27b84207bc2bbdb_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{sin(\frac{ax+bx}{2})sin(\frac{ax-bx}{2})}{sin^2(\frac{cx}{2})}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-24828515e2c8f08dcebba98353fbddfc_l3.png)
=![Rendered by QuickLaTeX.com \lim_{x\to0}[\frac{\frac{sin(\frac{ax+bx}{2})}{(\frac{ax+bx}{2})}×(\frac{ax+bx}{2})×\frac{sin(\frac{ax-bx}{2})}{(\frac{ax-bx}{2})}×\frac{ax-bx}{2}}{(\frac{sin\frac{cx}{2}}{\frac{cx}{2}})^2×(\frac{cx}{2})^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b555a1b6e1e373cbc4c48cebf2a6ef6f_l3.png)
= [(a + b)(a – b)/c2] × (4/4)
= (a2 – b2)/c2
Question 62. limh→0[{(a + h)2sin(a + h) – a2sina}/h]
Solution:
We have,
limh→0[{(a + h)2sin(a + h) – a2sina}/h]
= limh→0[{(a+h)2(sina.cosh)+(a+h)2(cosa.sinh)-a2sina}/h]
= limh→0[{(a2+2ah+h2)(sina.cosh)-a2sina+(a+h)2(cosa.sinh)}/h]
= limh→0[{a2sina(cosh-1)+2ah.sina.cosh+h2sina.cosh+(a+h)2cosa.sinh}/h]
= limh→0[{a2sina(-2sin2(h/2))+2ah.sina.cosh+h2sina.cosh+(a+h)2cosa.sinh}/h]
=![Rendered by QuickLaTeX.com \lim_{h\to0}[\frac{-a^2sina*sin^2(\frac{h}{2})}{\frac{h}{2}}+2asina.cosh+hsina.cosh+(a+h)^2cosa.sinh]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1be3331e107480fbc244a00e71c47346_l3.png)
= 0 + 2asina + 0 + a2cosa
= 2a + a2cosa
Question 63. If limx→0[kx.cosecx] = limx→0[x.coseckx], find K.
Solution:
We have,
limx→0[kx.cosecx] = limx→0[x.coseckx]
limx→0[kx/sinx] = limx→0[x/sinkx]
klimx→0[x/sinx] = limx→0[kx/sinkx](1/k)
k = (1/k)
k2 = 1
k = ±1
Share your thoughts in the comments
Please Login to comment...