Class 11 RD Sharma Solutions – Chapter 18 Binomial Theorem- Exercise 18.2 | Set 3
Last Updated :
16 May, 2021
Question 27. If the 3rd, 4th, 5th and 6th terms in the expansion of (x + α)n be respectively a, b, c, and d, prove that 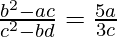 .
.
Solution:
We are given, (x + α)n
So, T3 = a = nC2 xn-2 α2
T4 = b = nC3 xn-3 α3
T5 = c = nC4 xn-4 α4
T6 = d = nC5 xn-5 α5
We need to prove that, 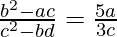
=> 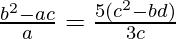
=> 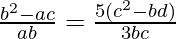
=> ![Rendered by QuickLaTeX.com \frac{b}{a}-\frac{c}{b}=\frac{5}{3}\left[\frac{c}{b}-\frac{d}{c}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-26367f4ff710e02ac3d48d5683508094_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{^nC_3x^{n-3}α^3}{^nC_2x^{n-2}α^2}-\frac{^nC_4x^{n-4}α^4}{^nC_3x^{n-3}α^3}=\frac{5}{3}\left[\frac{^nC_4x^{n-4}α^4}{^nC_3x^{n-3}α^3}-\frac{^nC_5x^{n-5}α^5}{^nC_4x^{n-4}α^4}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ea88f7c6275becc000fa4217581fa3c0_l3.png)
=> ![Rendered by QuickLaTeX.com \left[\frac{^nC_3}{^nC_2}-\frac{^nC_4}{^nC_3}\right]\frac{\alpha}{x}=\frac{5\alpha}{3x}\left[\frac{^nC_4}{^nC_3}-\frac{^nC_5}{^nC_4}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-47c579f2c217bc5b9799a92454d8fb8b_l3.png)
=> ![Rendered by QuickLaTeX.com \left[\frac{n-2}{3}-\frac{n-3}{4}\right]=\frac{5}{3}\left[\frac{n-3}{4}-\frac{n-4}{5}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0d079a3485158687aed1c7cd3bd2b568_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{4n-8-3n+9}{12}=\frac{5}{3}\left[\frac{5n-15-4n+16}{20}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ef77c82151a48b2d5d935e8609022180_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{n+1}{12}=\frac{5}{3}\left[\frac{n+1}{20}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-34b7e5e8a070d70dc1dcd137be14acd4_l3.png)
=> 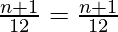
Hence proved.
Question 28. If the 6th, 7th, 8th and 9th terms in the expansion of (x + α)n be respectively a, b, c, and d, prove that 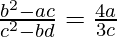 .
.
Solution:
We are given, (x + α)n
So, T6 = a = nC5 xn-5 α5
T7 = b = nC6 xn-6 α6
T8 = c = nC7 xn-7 α7
T9 = d = nC8 xn-8 α8
We need to prove that, 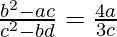
=> 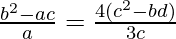
=> 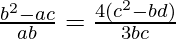
=> ![Rendered by QuickLaTeX.com \frac{b}{a}-\frac{c}{b}=\frac{4}{3}\left[\frac{c}{b}-\frac{d}{c}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a2304c7a9e966f38eeade5ded2ada6e5_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{^nC_6x^{n-6}α^6}{^nC_5x^{n-5}α^5}-\frac{^nC_7x^{n-7}α^7}{^nC_6x^{n-6}α^6}=\frac{4}{3}\left[\frac{^nC_7x^{n-7}α^7}{^nC_6x^{n-6}α^6}-\frac{^nC_8x^{n-8}α^8}{^nC_7x^{n-7}α^7}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-15b60323398b553be539e9ae5c452a5d_l3.png)
=> ![Rendered by QuickLaTeX.com \left[\frac{^nC_6}{^nC_5}-\frac{^nC_7}{^nC_6}\right]\frac{\alpha}{x}=\frac{4\alpha}{3x}\left[\frac{^nC_7}{^nC_6}-\frac{^nC_8}{^nC_7}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-353679c8e55b01d41501ca99cf256db1_l3.png)
=> ![Rendered by QuickLaTeX.com \left[\frac{n-5}{6}-\frac{n-6}{7}\right]=\frac{4}{3}\left[\frac{n-6}{7}-\frac{n-7}{8}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-25bd4f07894d451df3ab543892a89f3d_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{7n-35-6n+36}{42}=\frac{4}{3}\left[\frac{8n-48-7n+49}{56}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f922aed9d50675aed93eb85588eaedac_l3.png)
=> ![Rendered by QuickLaTeX.com \frac{n+1}{42}=\frac{4}{3}\left[\frac{n+1}{56}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3939e1f6cb0067fe76d318c9c1ac763c_l3.png)
=> 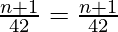
Hence proved.
Question 29. If the coefficients of three consecutive terms in the expansion of (1+x)n are respectively 76, 95, and 76, find n.
Solution:
We are given, (1+x)n
Let the three consecutive terms be rth, (r+1)th and (r+2)th.
We know the coefficient of rth term of a binomial expression is given by nCr-1.
Coefficient of rth term = nCr-1 = 76
Coefficient of (r+1)th term = nCr+1-1 = nCr = 95
Coefficient of (r+2)th term = nCr+2-1 = nCr+1 = 76
Now, 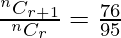
=> 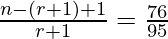
=> 
=> 5n − 5r = 4r + 4
=> 5n − 9r = 4 . . . . (1)
Also, 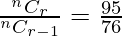
=> 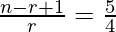
=> 4n − 4r + 4 = 5r
=> 4n − r = −4 . . . . (2)
Subtracting (2) from (1), we get,
=> n = 4 + 4
=> n = 8
Therefore, the value of n is 8.
Question 30. If the 6th, 7th, and 8th in the expansion of (x + a)n be respectively 112, 7, and 1/4, find x, a, and n.
Solution:
We are given, (x + a)n
Also, T6 = nC5 xn-5 a5 = 112
T7 = nC6 xn-6 a6 = 7
T8 = nC7 xn-7 a7 = 1/4
Now, 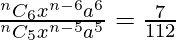
=> 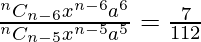
=> 
=> 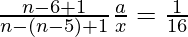
=> 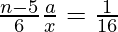
=> 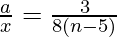 . . . . (1)
. . . . (1)
Also, 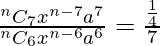
=> 
=> 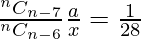
=> 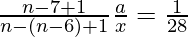
=> 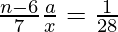
=> 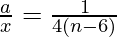 . . . . (2)
. . . . (2)
From (1) and (2), we get,
=> 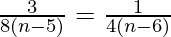
=> 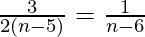
=> 3n − 18 = 2n − 10
=> n = 8
Putting n = 8 in (2), we get,
=> 
=> 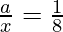
=> x = 8a
Now, nC5 xn-5 a5 = 112
=> 8C5 x8-5 a5 = 112
=> 8C5 (8a)3 a5 = 112
=> 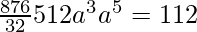
=> a8 = 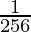
=> a8 = 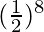
=> a = 1/2
So, x = 8 (1/2) = 4
Therefore, the value of x, a and n is 4, 1/2 and 8 respectively.
Question 31. If the 2nd, 3rd, and 4th in the expansion of (x + a)n be respectively 240, 720, and 1080 respectively, find x, a, and n.
Solution:
We are given, (x + a)n
Also, T2 = nC1 xn-1 a = 240
T3 = nC2 xn-2 a2 = 720
T4 = nC3 xn-3 a3 = 1080
Now, 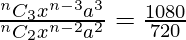
=> 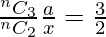
=> 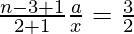
=> 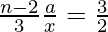
=> 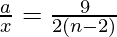 . . . . (1)
. . . . (1)
Also, 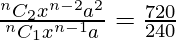
=> 
=> 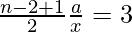
=> 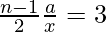
=> 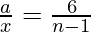 . . . . (2)
. . . . (2)
From (1) and (2), we get,
=> 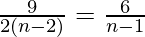
=> 12n − 24 = 9n − 9
=> 3n = 15
=> n = 5
Putting n = 5 in (2), we get,
=> 
=> 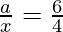
=> 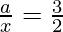
=> 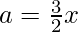
Now, nC1 xn-1 a = 240
=> 5C1 x5-1 (3x/2) = 240
=> 5C1 x5 (3/2) = 240
=> 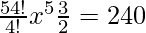
=> 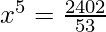
=> x5 = 32
=> x5 = 25
=> x = 2
So, a = (3/2) (2) = 3
Therefore, the value of x, a and n is 2, 3 and 5 respectively.
Question 32. Find a, b, and n in the expansion of (a+b)n if the first three terms are 729, 7290, and 30375 respectively.
Solution:
We are given, (a+b)n
Also, T1 = nC0 an = 729
T2 = nC1 an-1 b1 = 7290
T3 = nC2 an-2 b2 = 30375
Now, 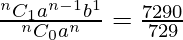
=> 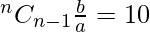
=> 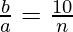 . . . . (1)
. . . . (1)
Also, 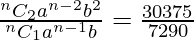
=> 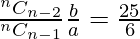
=> 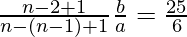
=> 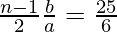
=>  . . . . (2)
. . . . (2)
From (1) and (2), we get,
=> 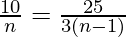
=> 30n − 30 = 25n
=> 5n = 30
=> n = 6
So, nC0 an = 729
=> a6 = 36
=> a = 3
Putting a = 3 in (2), we get,
=> 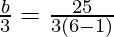
=> 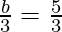
=> b = 5
Therefore, the value of a, b and n is 3, 5 and 6 respectively.
Question 33. Find a, if the coefficients of x2 and x3 in the expansion of (3+ax)9 are equal.
Solution:
We have, (3+ax)9 = 9C0 39 + 9C1 38 (ax)1 + 9C2 37 (ax)2 + 9C3 36 (ax)3 + . . . .
Coefficient of x2 = 9C2 37 a2
Coefficient of x3 = 9C3 36 a3
According to the question, we have,
=> 9C2 37 a2 = 9C3 36 a3
=> 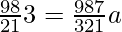
=> 81 = 63 a
=> a = 9/7
Therefore, the value of a is 9/7.
Question 34. Find a, if the coefficients of x and x3 in the expansion of (2+ax)4 are equal.
Solution:
We have, (2+ax)4 = 4C0 24 + 4C1 23 (ax)1 + 4C2 22 (ax)2 + 4C3 2 (ax)3 + . . . .
Coefficient of x = 4C1 23 a
Coefficient of x3 = 4C3 2 a3
According to the question, we have,
=> 4C1 23 a = 4C3 2 a3
=> 4C3 23 a = 4C3 2 a3
=> 8a = 2a3
=> 2a (a − 4) = 0
=> a = 0 or a = 4
Therefore, the value of a is 0 or 4.
Question 35. If the term free from x in the expansion of 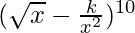 is 405, find the value of k.
is 405, find the value of k.
Solution:
We have, 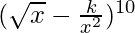
The general term of this expression will be,
Tr+1 = 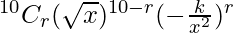
= 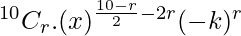
If the term is independent of x , we must have,
=> 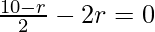
=> 10 − r − 4r = 0
=> 5r = 10
=> r = 2
Therefore, the required term is 3rd term.
So, we have,
=> 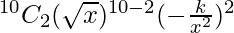 = 405
= 405
=> 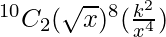 = 405
= 405
=> 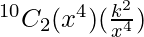 = 405
= 405
=> 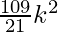 = 405
= 405
=> 45k2 = 405
=> k2 = 9
=> k = 3
Therefore, the value of k is 3.
Question 36. Find the sixth term in the expansion (y1/2 + x1/3)n, if the binomial coefficient of the third term from the end is 45.
Solution:
We have, (y + x)n
The third term of the expansion from the end is (n + 1 − 3 + 1)th term = (n − 1)th term.
=> Tn-1 = Tn-2+1 = nCn-2 (y1/2)n-(n-2) (x1/3)n-2
The coefficient of this term is given, i.e., 45.
=> nCn-2 = 45
=> n (n − 1)/2 = 45
=> n (n − 1) = 90
=> n2 − n − 90 = 0
=> n2 − 10n + 9n − 90 = 0
=> n(n−10) + 9 (n−10) = 0
=> n = 10 or n = −9 (ignored)
So, the sixth term of the expansion is T6 = T5+1
= 10C10-5 (y1/2)10-(10-5) (x1/3)10-5
= 10C5 (y1/2)5 (x1/3)5
= 252 (y5/2) (x5/3)
Question 37. If p is a real number and if the middle term in the expansion of (p/2 + 2)8 is 1120, find p.
Solution:
We have, (p/2 + 2)8
Total number of terms is 8 + 1 = 9 (odd number).
The middle term is (9+1)/2 = 5th term.
Therefore, we get T5 = T4+1 = 1120
=> 8C4 (p/2)8-4 (2)4 = 1120
=> 70 (p/2)4 (2)4 = 1120
=> 70p4 = 1120
=> p4 = 16
=> p4 = 24
=> p = 2
Therefore, the value of p is 2.
Question 38. Find n in the binomial ![Rendered by QuickLaTeX.com (\sqrt[2]2+\frac{1}{\sqrt[3]3})^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5f8bc5343843c39d93c06209b39fb4ae_l3.png) , if the ratio of the 7th term from the beginning to from the end is 1/6.
, if the ratio of the 7th term from the beginning to from the end is 1/6.
Solution:
We have, ![Rendered by QuickLaTeX.com (\sqrt[2]2+\frac{1}{\sqrt[3]3})^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fbb4c0014673dc65537381bc3346ccf8_l3.png)
7th term from the beginning is ![Rendered by QuickLaTeX.com ^nC_6(\sqrt[3]2)^{n-6}(\frac{1}{\sqrt[3]3})^6](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f9e6b06b0a7a624d637358b90b8379e8_l3.png) .
.
And 7th term from the end is ![Rendered by QuickLaTeX.com ^nC_{n-6}(\sqrt[3]2)^{6}(\frac{1}{\sqrt[3]3})^{n-6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d41fde205e7750713c971cde9f382b61_l3.png) .
.
According to the question, we have,
=> ![Rendered by QuickLaTeX.com \frac{^nC_6(\sqrt[3]2)^{n-6}(\frac{1}{\sqrt[3]3})^6}{^nC_{n-6}(\sqrt[3]2)^{6}(\frac{1}{\sqrt[3]3})^{n-6}}=\frac{1}{6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a3a374c8c30643b8bc42c5badbc383fb_l3.png)
=> ![Rendered by QuickLaTeX.com (\sqrt[3]2)^{n-12}(\frac{1}{\sqrt[3]3})^{12-n}=\frac{1}{6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ddf8a7d79438e84eb525d8c76b57b411_l3.png)
=> ![Rendered by QuickLaTeX.com (\sqrt[3]2)^{n-12}(\sqrt[3]3)^{n-12}=\frac{1}{6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a9f16fd4fe00cad9ca9eac677748577f_l3.png)
=> 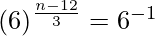
=> (n − 12)/3 = −1
=> n − 12 = −3
=> n = 9
Therefore, the value of n is 9.
Question 39. If the seventh term from the beginning and end in the binomial expansion of ![Rendered by QuickLaTeX.com (\sqrt[2]2+\frac{1}{\sqrt[3]2})^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c519799f00f02cd31482b78b0c73db6f_l3.png) are equal, find n.
are equal, find n.
Solution:
We have, ![Rendered by QuickLaTeX.com (\sqrt[2]2+\frac{1}{\sqrt[3]2})^n](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-891cc48b71ec9e3b04ccbb193f9c310a_l3.png)
7th term from the beginning is ![Rendered by QuickLaTeX.com ^nC_6(\sqrt[3]2)^{n-6}(\frac{1}{\sqrt[3]2})^6](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4440348e7fc2accdf1f51c7da529b576_l3.png) .
.
And 7th term from the end is ![Rendered by QuickLaTeX.com ^nC_{n-6}(\sqrt[3]2)^{6}(\frac{1}{\sqrt[3]2})^{n-6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9b0c31f3fc2b03946c58a7c330ad5b05_l3.png) .
.
According to the question, we have,
=> ![Rendered by QuickLaTeX.com ^nC_6(\sqrt[3]2)^{n-6}(\frac{1}{\sqrt[3]2})^6 = \hspace{0.1cm}^nC_{n-6}(\sqrt[3]2)^{6}(\frac{1}{\sqrt[3]2})^{n-6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-581d45cd3f70b930a25374d4af445347_l3.png)
=> ![Rendered by QuickLaTeX.com (\sqrt[3]2)^{n-12}=(\sqrt[3]2)^{12-n}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1864c2da987df74259b55bd3b48f7b44_l3.png)
=> n − 12 = 12 − n
=> 2n = 24
=> n = 12
Therefore, the value of n is 12.
Share your thoughts in the comments
Please Login to comment...