Whenever an experiment is performed whose outcomes cannot be predicted with certainty, it is called a random experiment. In such cases, we can only measure which of the events is more likely or less likely to happen. This likelihood of events is measured in terms of probability and events refer to the possible outcomes of an experiment. Also, events can be classified into various different types based on different properties and probability values of events.
In this article, we’ll explore the various types of events in probability, including simple events, compound events, mutually exclusive events, independent events, and dependent events. So, let’s dive into the world of different types of events.
What are Events?
An event is described as a set of outcomes. For example, getting a tail in a coin toss is an event and all the even-numbered outcomes while rolling a die also constitute an event.
An event is a subset of the sample space.
Consider an experiment of throwing a die. Let’s say that event E is defined as getting an even number. So, if a number 4 comes up, it is said that event E has occurred.
So, an event E of a sample space S is said to have occurred if the outcome w of the experiment is such that w ∈ E. When an outcome is such that it does not belong to the set E. It is said to have not occurred.
Type of Events
It is now clear that events are subsets of sample space. It is essential to understand the difference between different types of events that can happen while performing random experiments. This understanding of events helps us in calculating the probabilities for both simple and complex random experiments. We know that events are basically set, so they can be classified on the basis of the elements they have. The following list gives the different types of events:
- Impossible and Sure Events
- Simple Event and Compound Event
- Dependent and Independent Events
- Mutually Exclusive Events
- Exhaustive Events
- Equally Likely Events
Let’s see them one by one.
Also, Read, Events in Probability
Impossible Event
To get an intuition for this type of event, consider an experiment in which we roll a die. Now let’s define an event that consists of outcomes that are multiple of 7. Sample space for this event is denoted by S,
S = {1, 2, 3, 4, 5, 6}
Now since there is no outcome in the sample space which is a multiple of 7. So, the set of event E will be an empty set.
These kinds of events are impossible and can be described by an empty set ∅ and are called Impossible Events.
Sure Event
Such an event which has a probability of 1 i.e., occurrence of the event is certain or universal truth then that event is called Sure Event or Certain Event. For example, If we roll a die, as the event is the occurrence of a number less than 7, then it is sure that the occurring number is always less than 7 as the die only has numbers 1, 2, 3, 4, 5, and 6.
Note: The collection of elements from sample space in Sure Event is the complete Sample Space.
Simple Event
Any event that comprises a single result from the sample space is known as a simple event.
For instance, the Sample space of rolling a die, S= {1, 2, 3, 4, 5, 6} and the event for getting less than 2, E= {1}, where E has a single result taken from the sample space, Hence the event is a Simple event.
Compound Event
A Compound event is just opposite to what a simple event is, that is, any event that comprises more than a single result or more than a single point from the sample space, that event is known as a Compound event.
For instance, S={1, 2, 3, 4, 5, 6} and E= {3, 4, 5}, where E is a Compound event.
Dependent Events
Dependent events are those in which the next outcome depends on the previous outcomes, which means, the probability of an event will change based on its previous outcomes.
For instance, let’s take the example of drawing balls from a bag, there are 4 black and 3 red balls in a bag, a ball is drawn, and it came out to be black (In the first draw, the probability of a black ball was 4/7= 0.571. When a ball is drawn the next time, the probability of the black ball occurring will change as now there are fewer balls in the bag (3 black and 3 red balls are left), hence, the probability of getting a black ball will be 3/6= 0.5. Thus, this event is dependent as the probability of each successive event depends upon the previous event.
Note : In the example above, there is a way of converting this dependent event into independent event, it can be done through Replacement. If after each experiment the ball is again kept in the bag, the sample space of the experiment will not change and hence, the probability of the event will remain same too.
Independent Event
Independent events are those in which the next outcome is independent of the previous outcome. This means the probability of the occurrence of an event will remain the same no matter how many times the same experiment is done.
For instance, let’s take the example of rolling a die, a die is rolled once and the probability of getting an even number is 0.5, now the dice is rolled again, still the probability of getting an even number will be 0.5 only. This means, that the probability of the event is independent of its previous outcomes.
Learn more about, Dependent and Independent Events
Equally Likely Events
Those outcomes of an experiment that have the same probability are called Equally Likely Events. In other words, if two or more events have the same likelihood of happening, they are considered equally likely events.
For example, consider rolling a fair six-sided die. Each of the six possible outcomes (1, 2, 3, 4, 5, and 6) has the same probability of occurring, which is 1/6. Therefore, rolling a 1 is equally likely as rolling a 2, 3, 4, 5, or 6.
Similarly, consider drawing a card from a standard deck of 52 cards. There are 13 cards of each suit (hearts, diamonds, clubs, and spades) and 4 cards of each rank (ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, jack, queen, and king). Therefore, the probability of drawing any particular card is 1/52, and the probability of drawing any particular suit or rank is 1/4.
Algebra of Events
Two or more sets can be combined using four different operations, union, intersection, difference, and compliment. Since events are nothing but subsets of sample space, which means they are also set by themselves. In the same manner, two or more events can be combined using these operations. Let’s consider three events A, B, and C defined over the sample space S.
Complimentary Event
For every event A, there exists another event A’, which is called a complimentary event. It consists of all those elements which do not belong to event A. For example, in the coin-tossing experiment. Let’s say event A is defined as getting one head.
So, A = {HT, TH, HH}
The complementary A’ of event A will be consists of all the elements in the sample space which are not in event A. Thus,
A’ = {TT}

Event A or B
The Union of two sets A and B is denoted as A ∪ B. This contains all the elements which are in either set A, set B, or both. This event A or B is defined as,
Event A or B = A ∪ B
OR
A ∪ B = {w : w ∈ A or w ∈ B}
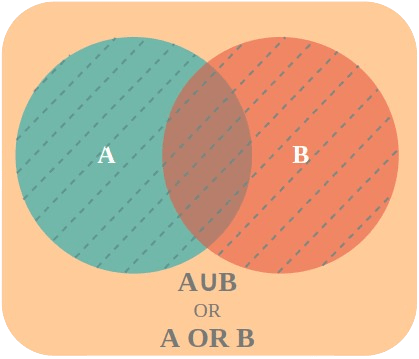
Events A and B
The intersection of two sets A and B is denoted as A ∩ B. This contains all the elements which are in both set A and set B. This event A and B is defined as,
Event A and B = A ∩ B
OR
A ∩ B= {w: w ∈ A and w ∈ B}

Event A but not B
The set difference A – B consists of all the elements which are in A but not in B. The events A but not B are defined as,
A but not B = A – B
OR
A – B = A ∩ B’
Where B’ is the complement of event B.
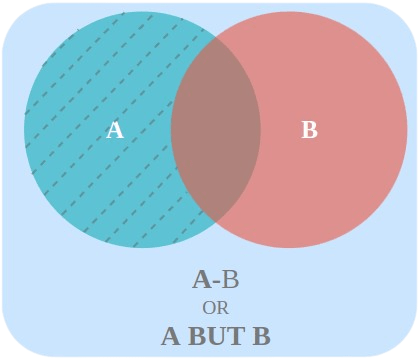
Using these concepts two other types of events are defined, that are:
- Mutually Exclusive Events
- Exhaustive Events
Let’s understand these two events as follows:
Mutually Exclusive Events
If the two events have nothing in common, then they are called mutually exclusive events, mutually exclusive events are similar to mutually exclusive sets. Formally two events A and B are called mutually exclusive if both of them cannot occur simultaneously. In this case, sets A and B are disjoint.
A ∩ B = ∅
For example, consider rolling a die,
S = {1, 2, 3, 4, 5, 6}
Now, event A is defined as “getting an even number” while event B is defined as “getting an odd number”. Now, these two events cannot occur together.
A = {2, 4, 6} and B = {1, 3, 5}.
Thus, the intersection between these two sets is an empty set.
Exhaustive Events
Exhaustive events are those mutually exclusive events that together cover all the possible outcomes of an experiment. In other words, when all possible outcomes of an experiment are listed, and no other outcome exists outside of the list, it is said to be exhaustive. Formally we can define exhaustive events as let’s consider three events A, B, and C will be called exhaustive events if,
A ∪ B ∪ C = S
In a more general setting, n events such that E1, E2,. . ., En is called exhaustive events if,
E1 ∪ E2 ∪. . .∪ En = S
As an example, let’s say for a two-times coin toss experiment,
A = Getting at least One head.
B = Getting two tails.
A = {HT, TH, HH} and B = {TT}
Thus, A ∪ B = S
Read More,
Sample Problems on Types of Events
Problems 1: Consider the experiment of tossing a fair coin 3 times, Event A is defined as getting all tails. What kind of event is this?
Solution:
Sample space for the coin toss will be,
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}
For the event A,
A = {TTT}
This event is only mapped to one element of sample space. Thus, it is a simple event.
Problems 2: Let’s say a coin is tossed once, state whether the following statement is True or False.
“If we define an event X which means getting both heads and tails. This event will be a simple event.”
Solution:
When a coin it tossed, there can be only two outcomes, Heads or Tails.
S = {H, T}
Getting both Heads and Tails is not possible, thus event X is an empty set.
Thus, it is an impossible and sure event. So, this statement is False.
Problems 3: A die is rolled, and three events A, B, and C are defined below:
- A: Getting a number greater than 3
- B: Getting a number that is multiple of 3.
- C: Getting an odd number
Find A ∩ B, A ∩ B ∩ C, and A ∪ B.
Solution:
Sample space for die roll will be,
S = {1, 2, 3, 4, 5, 6}
For the event A,
A = {4, 5, 6}
For the event B,
B = {3, 6}
For the event C,
C = {1, 3, 5}
A ∩ B = {4, 5, 6} ∩ {3, 6}
⇒ A ∩ B = {6}
A ∩ B ∩ C = {4, 5, 6} ∩ {3, 6} ∩ {1, 3, 5}
⇒ A ∩ B ∩ C = ∅ (Empty Set)
A ∪ B = {4, 5, 6} ∪ {3, 6}
⇒ A ∪ B = {3, 4, 5, 6}
Problems 4: A die is rolled, let’s define two events, event A is getting the number 2 and Event B is getting an even number. Are these events mutually exclusive?
Solution:
Sample space for die roll will be,
S = {1, 2, 3, 4, 5, 6}
For the event A,
A = {2}
For the event B,
B = {2, 4, 6}
For two events to be mutually exclusive, their intersection must be an empty set
A ∩ B = {2} ∩ {2, 4, 6}
⇒ A ∩ B = {2}
Since it is not an empty set, these events are not mutually exclusive.
FAQs on Types of Events in Probability
Q1: What is an Event in Probability?
Answer:
An event in probability is a set of outcomes of a random experiment or in other words, an event in probability is the subset of the sample space.
Q2: What are the Different Types of Events in Probability?
Answer:
The different types of events in probability are as follows:
- Impossible and Sure Events
- Simple Event and Compound Event
- Dependent and Independent Events
- Mutually Exclusive Events
- Exhaustive Events
- Equally Likely Events
Q3: What is a Simple Event?
Answer:
A simple event is an event that consists of a single outcome. For example, if a coin is tossed, the event of getting a head is a simple event.
Q4: What is a Compound Event?
Answer:
A compound event is an event that consists of two or more outcomes. For example, when rolling two dice and getting a sum of 7 which can be achieved either by (1, 6), (2, 5), (3, 4), (4, 3), (3, 4), (5, 2), or (6, 1).
Q5: What is a Complementary Event?
Answer:
Two disjoint events are called complementary events if their union is a complete sample space. For example, in a coin toss one event is getting a head and its complementary event is getting tails.
Q6: What is the Difference Between Mutually Exclusive Events and Independent Events?
Answer:
Those events which can’t occur simultaneously are called Mutually exclusive events whereas independent events are those events where the occurrence of one event doesn’t affect the probability of the other event.
Q7: What is the Difference Between Conditional Probability and Unconditional Probability?
Answer:
When the probability of an event is calculated without any prior knowledge of any event associated with it, then that probability is called unconditional probability whereas conditional probability is the probability of an event occurring given that another event has already occurred.
Share your thoughts in the comments
Please Login to comment...