Class 11 RD Sharma Solutions- Chapter 30 Derivatives – Exercise 30.1
Last Updated :
03 Jan, 2021
Question 1. Find the derivative of f(x) = 3x at x = 2
Solution:
Given: f(x)=3x
By using the derivative formula,
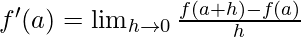 {where h is a small positive number}
{where h is a small positive number}
Derivative of f(x)=3x at x=2 is given as:
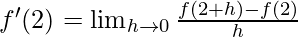
⇒ 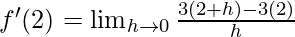
⇒ 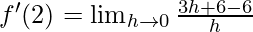
⇒ 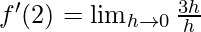
⇒ 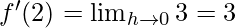
Hence, derivative of f(x)=3x at x=2 is 3
Question 2. Find the derivative of f(x) = x2– 2 at x = 10
Solution:
Given: f(x)= x2-2
By using the derivative formula,
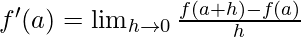 {where h is a small positive number}
{where h is a small positive number}
Derivative of f(x)=x2-2 at x=10 is given as:
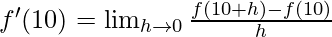
⇒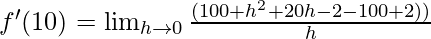
⇒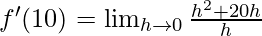
⇒
⇒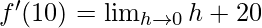
⇒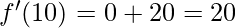
Hence, derivative of f(x)=x2-2 at x=10 is 20
Question 3. Find the derivative of f(x) = 99x at x = 100
Solution:
Given: f(x)= 99x
By using the derivative formula,
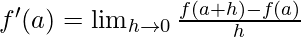 {where h is a small positive number}
{where h is a small positive number}
Derivative of f(x)=99x at x=100 is given as:
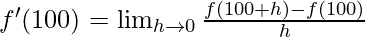
⇒ 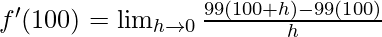
⇒ 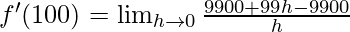
⇒ 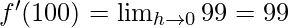
Hence, derivative of f(x)=99x at x=100 is 99
Question 4. Find the derivative of f(x) = x at x = 1
Solution:
Given: f(x)=x
By using the derivative formula,
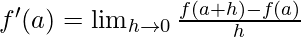 {where h is a small positive number}
{where h is a small positive number}
Derivative of f(x)=x at x=1 is given as:
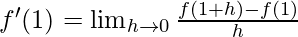
⇒ 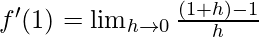
⇒ 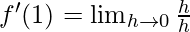
⇒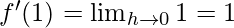
Hence, derivative of f(x)=x at x=1 is 1
Question 5. Find the derivative of f(x) = 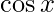 at x = 0
at x = 0
Solution:
Given: f(x)=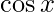
By using the derivative formula,
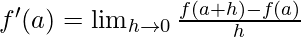 {where h is a small positive number}
{where h is a small positive number}
Derivative of f(x)=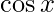 at x=0 is given as:
at x=0 is given as:
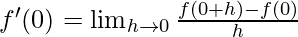
⇒ 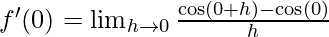
⇒ 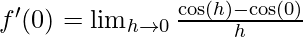
⇒ 
∵ we can not find the limit of the above function f(x)=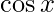 by direct substitution as it gives 0/0 form (indeterminate form)
by direct substitution as it gives 0/0 form (indeterminate form)
So we will simplify it to find the limit.
As we know that 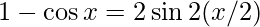
∴ 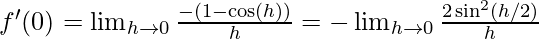
Divide the numerator and denominator by 2 to get the form 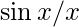 for applying sandwich theorem and multiplying h in numerator and denominator to get the required form.
for applying sandwich theorem and multiplying h in numerator and denominator to get the required form.
⇒ 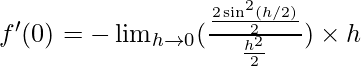
⇒ 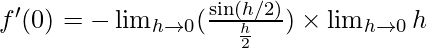
Using the formula: 
∴ 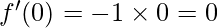
Hence, derivative of f(x)=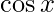 at x=0 is 0
at x=0 is 0
Question 6. Find the derivative of f(x) = 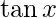 at x = 0
at x = 0
Solution:
Given: f(x)=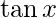
By using the derivative formula,
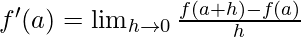 {where h is a small positive number}
{where h is a small positive number}
Derivative of f(x)=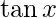 at x=0 is given as:
at x=0 is given as:
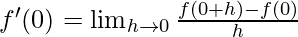
⇒ 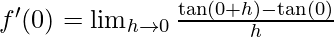
⇒ 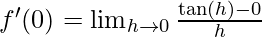
⇒ 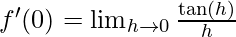
∴ Use the formula: 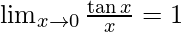 {sandwich theorem}
{sandwich theorem}
⇒ 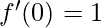
Hence, derivative of f(x)=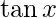 at x=0 is 1
at x=0 is 1
Question 7(i). Find the derivatives of the following functions at the indicated points : 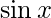 at
at 
Solution:
Given: f(x)= 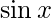
By using the derivative formula,
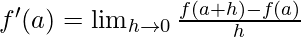 {where h is a small positive number}
{where h is a small positive number}
Derivative of f(x)=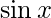 at
at  is given as:
is given as:
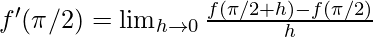
⇒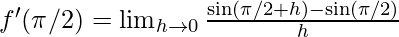
⇒ 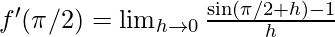
⇒ f'(\pi/2)= 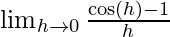 {∵
{∵
∵ we can not find the limit of the above function by direct substitution as it gives 0/0 form (indeterminate form)
So we will simplify it to find the limit.
As we know that
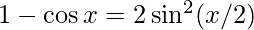
∴ 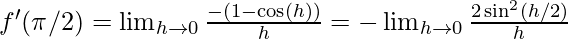
Divide the numerator and denominator by 2 to get the form (sin x)/x for applying sandwich theorem and multiplying h in numerator and denominator to get the required form.
⇒ 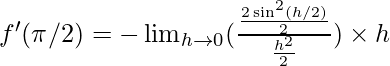
⇒ 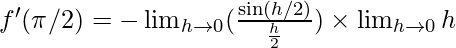
Using the formula:

∴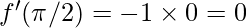
Hence, derivative of f(x)= 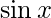 at
at  is 0
is 0
Question 7(ii). Find the derivatives of the following functions at the indicated points : x at x=1
Solution:
Given: f(x)=x
By using the derivative formula,
 {where h is a small positive number}
{where h is a small positive number}
Derivative of f(x)=x at x=1 is given as:
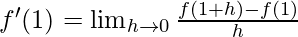
⇒ 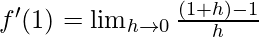
⇒ 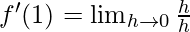
⇒ 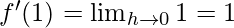
Hence, derivative of f(x)=x at x=1 is 1
Question 7(iii). Find the derivatives of the following functions at the indicated points : 2\cos x at 
Solution:
Given: f(x)= 
By using the derivative formula,
 {where h is a small positive number}
{where h is a small positive number}
Derivative of f(x)= 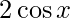 at
at  is given as:
is given as:
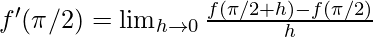
⇒ 
⇒ f'(\pi/2)= \lim_{h \to 0} \frac {-2\sin(h)} h {∵ 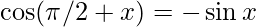 }
}
∵ we can not find the limit of the above function by direct substitution as it gives 0/0 form (indeterminate form)
∴ 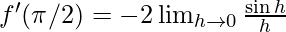
Using the formula: 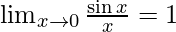
∴ 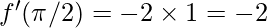
Hence, derivative of f(x)= 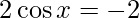
Question 7(iv). Find the derivatives of the following functions at the indicated points : 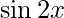 at
at 
Solution:
Given: f(x)= 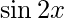
By using the derivative formula,
 {where h is a small positive number}
{where h is a small positive number}
Derivative of f(x)= 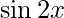 at
at  is given as:
is given as:
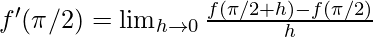
⇒ 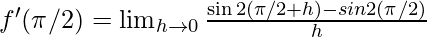
⇒ 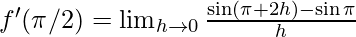 {∵
{∵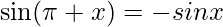 }
}
⇒ 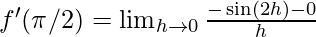
⇒ 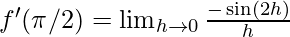
∵ we can not find the limit of the above function by direct substitution as it gives 0/0 form (indeterminate form)
Using the sandwich theorem and multiplying 2 in numerator and denominator to apply the formula.

Using the formula: 
∴ 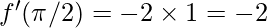
Hence, derivative of f(x)=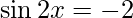
Share your thoughts in the comments
Please Login to comment...