General and Middle Terms – Binomial Theorem – Class 11 Maths

The binomial theorem or expansion describes the algebraic expansion of powers of a binomial. According to this theorem, it is possible to expand the polynomial “(a + b)^n“ into a sum involving terms of the form “ax^zy^c“, the exponents z and c are non-negative integers where z + c = n, and the coefficient of each term is a positive integer depending on the values of n and b. 

Example: If n = 4

(a + b)⁴ = a⁴ + 4a³y + 6a²b² + 4ab³ + b

General Term of Binomial Expansion

The General Term of Binomial Expansion of (x + y)ⁿ is as follows

• T_r+1 is the General Term in the binomial expansion
• The General term expansion is used to find the terms mentioned in the above formula.
• To find the terms in the binomial expansion we need to expand the given expansion.
• Suppose (a + b)ⁿ is the equation then the series of its binomial expansion will be as follows:

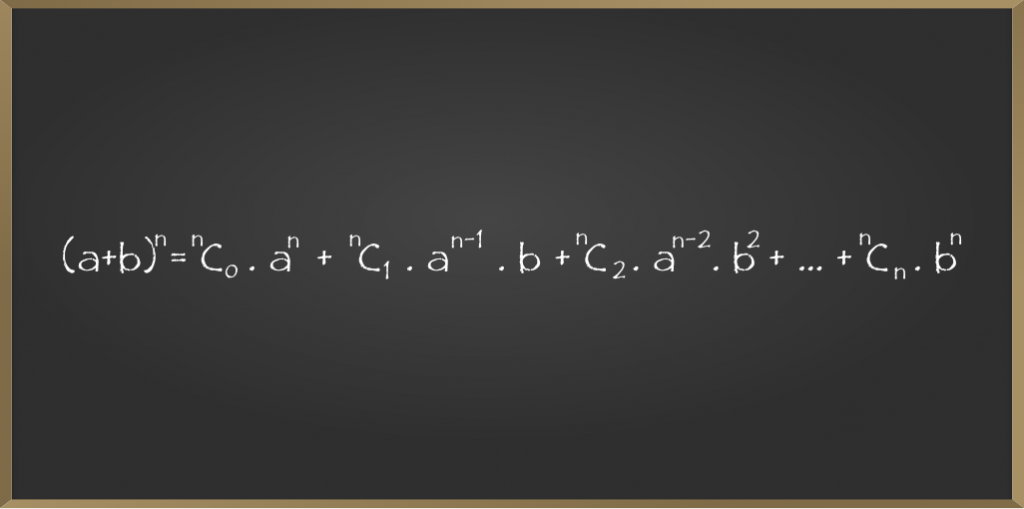
• The first term of the series is T₁ = ⁿC₀.aⁿ
• The second term of the series is T₂ = ⁿC₁.a^n-1.b
• The third term of the series is T₃ = ⁿC₂.a^n-2.b²
• The n^th term of the series is T_n= ⁿC_n.bⁿ

Sample Problems on General Term

Example 1: Find (r+1)^th  term for the given binomial expansion (x + 2y)⁵

Solution: 

Given expansion is (x + 2y)⁵

a = x, b= 2y, n = 5

The formula for (r+1)^th is  ⁿC_r .a^{n – r}.b^r

(r+1)^th term =⁵C_r.x^{5 -r}.2y^r

Example 2: Find (r+1)^th term for the given binomial expansion (a + 2b)⁷

Solution:

Given expansion is (a + 2b)⁷

a = a, b = 2b, n = 7

The formula for (r+1)th is  ⁿC_r .a^{n – r}.b^r

(r+1)^th term = ⁷C_r.a^{7 -r}.b^r

Example 3: Find (r + 1)^th term for the given binomial expansion (6p + 2q)¹²

Solution: 

Given expansion is  (6p + 2q)

a = 6p, b = 2q, n = 12

The formula for (r+1)^th is  ⁿC_r .a^{n – r}.b^r

(r + 1)^th term = ¹²C_r.6p^{12 -r}.2q^r

Middle Term of the Binomial Expansion

If (x + y)ⁿ =  ⁿC_r.x^{n – r.}y^r , it has (n + 1) terms and the middle term will depend upon the value of n.

We have two cases for the Middle Term of a Binomial Expansion:

If n is Even 

If n is the even number then we make it into an odd number and consider (n + 1) as odd and (n/2 + 1) as the middle term. In simple, if n is even then we consider it as odd.

Suppose n is the even so, (n + 1) is odd. To find out the middle term :

Consider the general term of binomial expansion i.e. 

• Now we replace “r ” with “n/2” in the above equation to find the middle term
• T_r+1 = T_n/2 + 1
• T_{n/2 + 1} = ⁿC_n/2.x^{n – n/2}.y^n/2

Sample Problems on Middle Terms

Example 1: Find the middle of the following binomial expansion (x + a)⁸

Solution:

Given expansion is (x + a)⁸

n = 8, we consider the expansion has (n + 1) terms so the above expansion has (8 + 1) i.e 9 terms 

we have T₁, T₂, T₃, T₄, T₅, T₆ , T₇, T₈, T₉.

T_r+1 = T_{n/2 + 1} = ⁿC_n/2.x^{n – n/2}.Y^n/2

T_{8/2 + 1} = ⁸C_8/2.x^8-8/2.a^8/2

T₅ = ⁸C₄.x⁴.a⁴ is the required middle term of the given binomial expansion.

Example 2: Find the middle of the following binomial expansion (x + 3y)⁶

Solution:

Given expansion is (x + 3y)⁶

n = 6, we consider the expansion has (n + 1) terms so the above expansion has (6 + 1) i.e 7 terms

we have T₁, T₂, T₃, T₄, T₅, T₆ , T₇.

T_r+1 = T_{n/2 + 1} = ⁿC_n/2.x^{n – n/2}.Y^n/2

T_{6/2 + 1} = ⁶C_6/2.x^6-6/2.3y^6/2

T₄ = ⁶C₃.x³.3y³ is the required middle term of the given binomial expansion.

Example 3: Find the middle of the following binomial expansion (2x + 5y)⁴

Solution: 

Given expansion is  (2x – 5y)⁴

n = 4, we consider the expansion has (n + 1) terms so the above expansion has (4 + 1) i.e 5 terms

we have T₁, T₂, T₃, T₄, T₅.

T_r+1 = T_{n/2 + 1} = ⁿC_n/2.x^{n – n/2}.Y^n/2

T_{4/2 + 1} = ⁴C_4/2.2x^4-4/2.5y^4/2

T₃ = ⁴C₂.x².5y² is the required middle term of the given binomial expansion.

If n is Odd

If n is the odd number then we make it into an even number and consider (n + 1) as even and (n + 1/2), (n + 3/2) as the middle terms. In simple, if n is odd then we consider it even.

We have two middle terms if n is odd. To find the middle term:

Consider the general term of binomial expansion i.e  

• In this case, we replace “r” with the two different values
• One term is (n + 1/2) compare with (r + 1) terms we get

r + 1 = n + 1/2

r = n + 1/2 -1

r = n -1/2

• Second middle term , compare (r + 1) with (n + 3/2) we get

r +1 = n +3/2

r = n + 3/2 – 1

r = n + 1/2

The two middle terms when n is odd are (n – 1/2) and (n + 1/2).

Sample Problems on Middle Terms

Example 1: Find the middle terms of the following binomial expansion (x + a)⁹

Solution: 

Given expansion is (x + a)⁹

a = x, b = a, and n = 9

Middle terms will be (n – 1)/2 and (n + 1)/2

T_{r + 1} =T _{n – 1/2} and T_{n + 1/2}

First middle term:

T_{r + 1} = T_{n – 1/2} = ⁹C_{(n – 1)/2}.x^{9 – (n – 1)/2}.a^{(n – 1)/2}

T_{(9 – 1/2)} = ⁹C_{(9 – 1)/2}.x^{9 – (n – 1)/2}.a^{(n – 1)/2}

T₄ = ⁹C₄.x⁵.a⁴

Second middle term: 

T_{r + 1} = T_{n + 1/2} =  ⁹C_{(n + 1)/2}.x^{9 – (n + 1)/2}.a^{(n + 1)/2}

T_{(9 + 1)/2} = ⁹C_{(9 + 1)/2}.x^{9 – (9 + 1)/2}.a^{(9 + 1)/2}

T₅ = ⁹C₅.x⁴.a⁵

The middle terms of expansion are T₄, and T_5.

Example 2: Find the middle terms of the following binomial expansion (4a + 9b)⁷

Solution: 

Given expansion is (4a + 9b)⁷

a = 4a,b = 9b, and n = 7

middle terms will be (n -1/2) and (n + 1/2) 

T_{r + 1} =T _{n – 1/2} and T_{n + 1/2}

First middle term:

T_{r + 1} = T_{n – 1/2} = ⁷C_{(n – 1)/2}.4a^{7 – (n – 1)/2}.9b^{(n – 1)/2}

T_{(7 – 1/2)} = ⁷C_{(7 – 1)/2}.4a^{7 – (7 – 1)/2}.9b^{(7 – 1)/2}

T₃ = ⁷C₃.4a⁴.9b³

Second middle term:

T_{r + 1} = T_{(n + 1)/2} =  ⁷C_{(n + 1)/2}.4a^{7 – (n + 1)/2}.9b^{(n + 1)/2}

T_{(7 + 1)/2} =  ⁷C_{(7 + 1)/2}.4a^{7 – (7 + 1)/2}.9b^{(7 + 1)/2}

T₄ = ⁷C₄.4a³.9b⁴

The middle terms of expansion are T₃, and T₄.

Example 3: Find the middle terms of the following binomial expansion (2x + 8y)⁵

Solution:

Given expansion is (2x + 8y)⁵

a = 2x,b = 8y, and n = 5

Middle terms will be (n – 1)/2 and (n + 1)/2 

T_{r + 1} = T _{(n – 1)/2} and T_{(n + 1)/2}

First middle term:

T_{r + 1} = T_{(n – 1)/2} = ⁵C_{(n – 1)/2}.2x^{5 – (n – 1)/2}.8y^{(n – 1)/2}

T_{(5 – 1)/2} = ⁵C_{(5 – 1)/2}.2x^{5 – (5 – 1)/2}.8y^{(5 – 1)/2}

T₂ = ⁵C₂.2x³.8y²

Second middle term:

T_{r + 1} = T_{(n + 1)/2} =  ⁵C_{(n + 1)/2}.2x^{5 – (n + 1)/2}.8y^{(n + 1)/2}

T_{(5 + 1)/2} =  ⁵C_{(5 + 1)/2}.2x^{5 – (5 + 1)/2}.8y^{(5 + 1)/2}

T₃ = ⁵C₃.2x².8y³

The middle terms of expansion are T₂, and T₃.