Question 17. Prove that:
(i) tan 8x – tan 6x – tan 2x = tan 8x tan 6x tan 2x
(ii) tan π/12 + tan π/6 + tan π/12 tan π/6 = 1
(iii) tan 36° + tan 9° + tan 36° tan 9° = 1
(iv) tan 13x – tan 9x – tan 4x = tan 13x tan 9x tan 4x
Solution:
(i) Prove: tan 8x – tan 6x – tan 2x = tan 8x tan 6x tan 2x
Proof:
Let’s solve LHS
= tan 8x – tan 6x – tan 2x
= tan 8x
= tan(6x + 2x)
As we know that
tan(A + B) = (tanA + tanB) / (1 – tanA tanB)
So,
= tan 8x (tan 6x + tan 2x)/(1 tan 6x tan 2x)
Now, by cross-multiplying we get,
= tan 8x (1 – tan 6x tan 2x) = tan 6x + tan 2x
= tan 8x – tan 8x tan 6x tan2x = tan 6x + tan 2x
After rearranging we get,
= tan 8x – tan 6x – tan 2x = tan 8x tan 6x tan 2x
= RHS
LHS = RHS
Hence proved.
(ii) Prove: tan π/12 + tan π/6 + tan π/12 tan π/6 = 1
Proof:
As we know that
π/12 15° and π/6 = 30°
So, we have 15° + 30° = 45°
tan (15° +30°) = tan 45°
Since, tan (A + B)= (tan A+ tan B) / (1 – tanA tanB)
So,
(tan 15°+tan 30°)/(1-tan 15° tan 30°) = 1
tan 15° tan 30° = 1 – tan 15° tan 30°
After rearranging we get,
tan15° + tan30° + tan 15° tan30° = 1
Hence proved.
(iii) Prove: tan 36° + tan 9° + tan 36° tan 9° = 1
Proof:
As we know that
36° + 9° = 45°
tan (36° + 9°) = tan 45°
Since, tan (A + B) = (tan A + tan B)/(1 – tanA tanB)
So,
(tan 36° + tan 9°)/(1 – tan 36° tan 9°) = 1
tan 36° + tan 9° = 1 – tan 36° tan 9°
After rearranging we get,
tan 36° + tan 9° + tan 36° tan 9° = 1 = RHS
LHS = RHS
Hence proved.
(iv) Prove: tan 13x-tan 9x-tan 4x = tan 13x tan 9x tan 4x
Proof:
Let solve LHS,
= tan 13x – tan 9x -tan 4x
⇒ tan 13x = tan (9x + 4x)
We know,
tan(A + B) = (tanA + tanB)/(1 – tanA tanB)
So,
tan 13x = (tan 9x + tan 4x)/(1 – tan 9x tan 4x)
Now by cross-multiplying we get,
tan 13x (1-tan 9x tan 4x) = tan 9x + tan 4x
tan 13x – tan 13x tan 9x tan 4x = tan 9x + tan 4x
After rearranging we get,
tan 13x – tan 9x – tan 4x = tan 13x tan 9x tan 4x = RHS
LHS = RHS
Hence proved.
Question 18. Proved that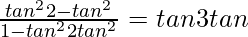
Solution:
Prove: 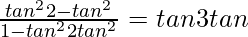
Proof:
Le’s solve RHS,
= tan3θ tanθ
= tan(2θ + θ) x tan(2θ – θ)
= ![Rendered by QuickLaTeX.com [\frac{tan2θ+tanθ}{1-tan2θtanθ}][\frac{tan2θ-tanθ}{1+tan2θtanθ}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e31e09850b17e92e980eec926f48e96d_l3.png)
= 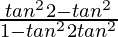
= LHS
LHS = RHS
Hence proved
Question 19. If 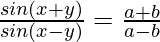 , show that tanx/tany = a/b
, show that tanx/tany = a/b
Solution:
Given that 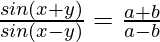
⇒ 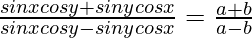
⇒ 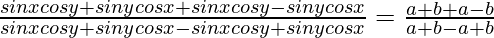
Now by using componendo and Dividendo, we get
⇒ 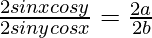
⇒ tanx/tany = a/b
Hence Proved.
Question 20. If tanA = x tanB, prove that 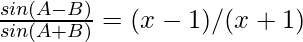
Solution:
Given that
tanA = x tanB
sinA/cosA = x sinB/cosB
⇒ sinAcosB = x cosA sinB
Now, 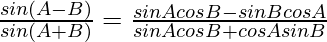
= 
= 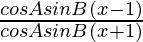
= (x – 1)(x + 1)
Hence Proved.
Question 21. If tan(A + B) = x and tan(A – B) = y, find the values of tan2A and tan2B.
Solution:
Given that
tan(A + B) = x and tan(A – B) = y
As we know that tan2A = tan[(A+B) + (A-B)]
= 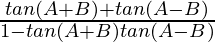
= (x + y) / (1 – xy)
Since, tan2B = tan[(A + B) – (A – B)]
So,
= 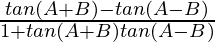
= (x – y) / (1 + xy)
Question 22. If cosA + sinB = m and sinA + sinB = n, prove that 2sin(A + B) = m2 + n2 – 2
Solution:
Given that
cosA + sinB = m and sinA + cosB = n
Prove: 2sin(A + B) = m2 + n2 – 2
Proof:
Let’s solve RHS, m2 + n2 – 2
= (cosA + sinB)2 + (sinA + cosB)2 – 2
= cos2A + sin2B + 2cosA sinB + sin2A + cos2B + 2 sinA cosB – 2
= (sin2A + cos2A) + (sin2B + cos2B) + 2 cosA sinB + 2 sinA cosB – 2
= 1 + 1 + 2 cosA sinB + 2 sinA cosB – 2
= 2 + 2(sinA cosB + cosA sinB) – 2
= 2(sinA cosB + cosA sinB)
= 2 sin(A + B)
LHS = RHS
Hence Proved.
Question 23. If tanA + tanB = a and cotA + cotB = b, prove that cot(A + B) = 1/a – 1/b.
Solution:
Given that
tanA + tanB = a and cotA + cotB = b
Prove: cot(A + B) = 1/a – 1/b.
Proof:
Lets solve cotA + cotB = b
⇒ 1/tanA + 1/tanB = b
⇒ (tanA + tanB)/(tanA tanB) = b
⇒ a/(tanA tanB) = b
⇒ a/b = tanA tanB
Now lwts solve LHS = cot(A + B) = 1/ tan(A + B)
= 1 / (tanA + tanB)/(1 – tanA tanB)
= (1 – tanA tanB)(tanA + tanB)
= (1 – a/b) / a
= (b-a)/ab
= b/ab – a/ab
= 1/a – 1/b
Hence proved.
Question 24. If θ lies in the first quadrant and cosθ = 8/17, then prove that:
cos(π/6 + θ) + cos(π/4 – θ) + cos(2π/3 – θ) = {(√3 – 1)/2 + 1/√2}23/17.
Solution:
Given,
0 < x < π/2
Now, sinx = 
Let’s solve LHS = cos(π/6 + x) + cos(π/4 – x) + cos(2π/3 – x)
= cos 30° cosx – sin 30° sinx + cos 45° cosx + sin 45° sinx +
cos 120° cosx + sin 120° sinx
= cosx (cos 30° + cos 45° + cos 120°) + sinx (- sin 30° + sin 45° + sin 120°)
= (8/17)(√3/2 + 1/√2 – 1/2) + (15/17)(-1/2 + 1/√2 + √3/2)
= (8/17)((√3-1)/2 + 1/√2) + (15/17)((√3 – 1)/2 + 1/√2)
= (23/17)((√3-1)/2 + 1/√2)
= RHS
LHS = RHS
Hence proved
Question 25. tanx + tan(x + π/3) + tan(x + 2π/3) = 3, then prove that (3tanx – tan3x)/(1 – 3tan2x) = 1
Solution:
Given,
tanx + tan(x + π/3) + tan(x + 2π/3) = 3
Prove: (3tanx – tan3x)/(1 – 3tan2x) = 1
Proof:
⇒ 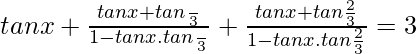
⇒ 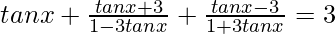
⇒ 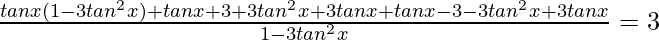
⇒ 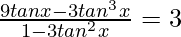
⇒ 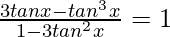
Hence proved.
Question 26. If sin(α + β) = 1 and sin(α – β) = 1/2, where 0 ≤ α, β ≤ π/2, then find the values of tan(α + 2β) and tan(2α + β)
Solution:
Given,
sin(α + β) = 1 and sin(α – β) = 1/2
Find the values of tan(α + 2β) and tan(2α + β)
So,
⇒ α + β = 90° …..(i)
and α – β = 30° …..(ii)
Now by adding eq (i) and eq (ii) we get,
⇒ 2α = 120°
⇒ α = 60°
And on subtracting eq (ii) from eq (i), we get,
⇒ 2β = 60°
⇒ β = 30°
So,
tan(α + 2β) = tan(60° + 2 × 30°) = tan120° = -√3
tan(2α + β) = tan(2 × 60° + 30°) = tan150° = -1/√3
Question 27. If α, β are two different values of x lying between 0 and 2π, which satisfy the equation 6cosx + 8sinx = 9, find the value of sin(α + β).
Solution:
Given,
6 cosx + 8 sinx = 9
⇒ 6 cosx = 9 – 8 sinx
⇒ 36 cos2x = (9 – 8 sinx)2
⇒ 36(1 – sin2x) = 81 + 64sin2x – 144 sinx
⇒ 100 sin2x – 144 sinx + 45 = 0
Now, let us considered α and β are the roots of the given equation,
So, cosα and cosβ are the roots of the above equation.
⇒ sinα sinβ = 45/100
Again,
6cosx + 8sinx = 9
⇒ 8sinx = 9 – 6 cosx
⇒ 64 sin2x = (9 – 6 cosx)2
⇒ 64(1 – cos2x) = 81 + 36 cos2x – 108 cosx
⇒ 100 cos2x – 108 cosx + 17 = 0
Now, let us considered α and β are the roots of the given equation,
So, sinα and sinβ are the roots of the above equation.
so, cosα cosβ = 17/100
Hence, cos(α + β) = cosα cosβ – sinα sinβ
= 17/100 – 45/100
= -28/100
= -7/25
sin(α + β) = √(1 – cos2(α + β))
= √(1 – (-7/25)2)
= √(576/625
= 24/25
Question 28 (i), If sinα + sinβ = a and cosα + cosβ = b, show that sin(α + β) = 2ab/(a2 + b2)
Solution:
Given that, sinα + sinβ = a and cosα + cosβ = b
Show : sin(α + β) = 2ab/(a2 + b2)
So, now solve b2 + a2 = (cosα + coβ)2 + (sinα + sinβ)2
= (cos2α + sin2α) + (sin2β + cos2β) + 2(cosα cosβ + sinα sinβ)
= 1 + 1 + 2 cos(α – β)
= 2 + 2 cos(α – β) ……..(i)
and,
b2 – a2 = (cosα + coβ)2 – (sinα + sinβ)2
= cos2α + cos2β – sin2α – sin2β + 2(cosα cosβ – sinα sinβ)
= (cos2α – sin2α) + (cos2β – sin2β) + 2 cos(α + β)
= 2cos(α + β)cos(α – β) + 2cos(α + β)
= cos(α + β){2cos(α – β) + 2}
= cos(α + β)(b2 + a2) …….(ii)
⇒ (b2 – a2)/(b2 + a2) = cos(α + β)
⇒ sin(α + β) = √(1 – cos2(α + β))
= 
= 2ab/(a2 + b2)
Question 28 (ii). If sinα + sinβ = a and cosα + cosβ= b, show that cos(α + β) = (b2 – a2)/(b2 + a2)
Solution:
Given that, sinα + sinβ = a and cosα + cosβ= b
Show: cos(α + β) = (b2 – a2)/(b2 + a2)
So, now solve b2 + a2 = (cosα + coβ)2 + (sinα + sinβ)2
= (cos2α + sin2α) + (sin2β + cos2β) + 2(cosα cosβ + sinα sinβ)
= 1 + 1 + 2 cos(α – β)
= 2 + 2 cos(α – β) ……(i)
and,
b2 – a2 = (cosα + coβ)2 – (sinα + sinβ)2
= cos2α + cos2β – sin2α – sin2β + 2(cosα cosβ – sinα sinβ)
= (cos2α – sin2α) + (cos2β – sin2β) – 2 cos(α + β)
= 2cos(α + β) cos(α – β) + 2cos(α – β)
= cos(α + β) {2cos(α – β) + 2} ……..(ii)
Now from (i) and (ii), we have
⇒ b2 – a2 = cos(α + β)(a2 + b2)
⇒ (b2 – a2)/(b2 + a2) = cos(α + β)
Question 29 (i). Proved that 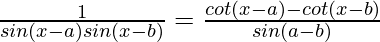
Solution:
Let’s solve RHS
= 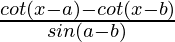
= 
= 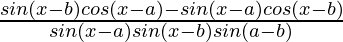
= 
= 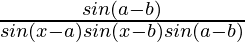
= 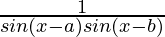
= LHS
LHS = RHS
Hence proved.
Question 29 (ii). Proved that 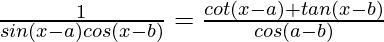
Solution:
Let’s solve RHS
= 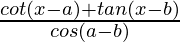
= 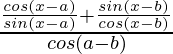
= 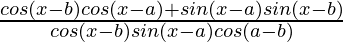
= 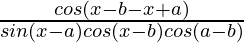
= 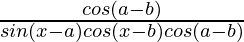
= 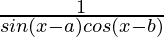
= RHS
LHS = RHS
Hence Proved.
Question 29 (iii). Proved that 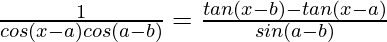
Solution:
Let’s solve RHS
= 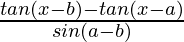
= 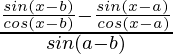
= 
= 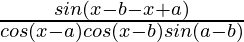
= 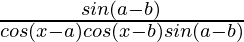
= 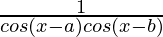
= LHS
LHS = RHS
Hence proved
Question 30. If sinα sinβ – cosα cosβ + 1 = 0, proved that 1 + cotα tanβ = 0
Solution:
Given,
sinα sinβ – cosα cosβ + 1 = 0
⇒ -(cosα cosβ – sinα sinβ) + 1 = 0
⇒ -cos(α + β) + 1 = 0
⇒ cos(α + β) = 1
Therefore, sin(α + β) = 0 ……(i)
Let’s solve LHS
= 1 + cotα tanβ = 1 + (cosα sinβ)/(sinα cosβ)
= (sinα cosβ + cosα sinβ)/ (sinα cosβ)
= sin(α + β)/ (sinα cosβ)
Now from eq(i), we get
= 0
LHS = RHS
Hence Proved.
Question 31. tanα = x + 1 and tanβ = x – 1, show that 2cot(α – β) = x2
Solution:
We have,
tanα = x + 1 and tanβ = x – 1
As we know that tan(α – β) = (tanα – tanβ) / (1 + tanα tanβ)
= [(x + 1) – (x – 1)] / [1 + (x + 1)(x – 1)]
= (x + 1 – x + 1) / (1 + x2 – 1)
= 2/ (1 + x2 – 1)
= 2/x2
cot(α – β) = x2/2
2cot(α – β) = x2
LHS = RHS
Hence Proved.
Question 32. If angle θ is divided into two parts such that the tangents of one part is λ part times the tangent of the other, and ϕ is their difference then show that sinθ = (λ + 1)/(λ – 1) sinϕ.
Solution:
Let us considered α and β be the two parts of the angle be θ.
Then, θ = α + β and ϕ = α – β
According to question, we get
tanα = λ tanβ
⇒ tanα / tanβ = λ/1
Now, applying componendo and dividendo, we get
⇒ (tanα + tanβ) / (tanα – tanβ) = (λ+1) / (λ-1)
⇒ 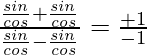
⇒ 
⇒ 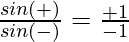
⇒ 
⇒ 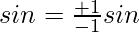
Hence proved.
Question 33. If tanθ = (sinα – cosα)/(sinα + cosα), then show that sinα + cosα = √2cosθ
Solution:
Given that tanθ = (sinα – cosα)/(sinα + cosα)
Now, on dividing both numerator and denominator by cosα, we get
⇒ tanθ = (tanα – 1)(tanα + 1)
⇒ tanθ = (tanα – tan(π/4))(1+tan(π/4)tanα)
⇒ tanθ = tan(α – π/4)
⇒ θ = (α – π/4)
Now Taking cos on both sides, we get
⇒ cosθ = cos(α – π/4)
⇒ cosθ = cosα.cos(π/4) + sinα.sin(π/4)
⇒ cosθ = cosα(1/√2) + sinα(1/√2)
⇒ cosθ = (cosα + sinα)/√2
⇒ √2cosθ = sinα + cosα
Hence Proved
Question 34. If tan(A + B) = p, tan(A – B) = q, then show that tan2A = (p + q)/(1 – pq)
Solution:
Given that, tan(A + B) = p, tan(A – B) = q
Now let’s solve RHS,
(p + q)/(1 – pq) = 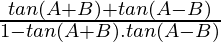
= 
= 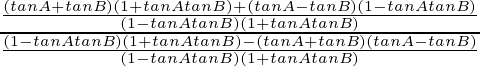
= 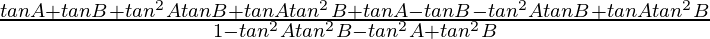
= 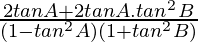
= 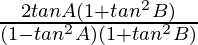
= 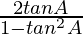
= tan2A = LHS
LHS = RHS
Hence Proved.
Share your thoughts in the comments
Please Login to comment...