Question 1. Find the equation of the parabola whose:
(i) Focus is (3, 0) and the directrix is 3x + 4y = 1
Solution:
Given that focus is (3, 0) and the directrix is 3x + 4y = 1
Let us assume that P (x, y) be any point on the parabola.
So, first we draw PM perpendicular to 3x + 4y = 1.
Then,
SP = PM
SP2 = PM2
(x – 3)2 + (y – 0)2 = 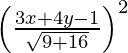
(x – 3)2 + y2 = 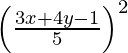
25 (x2 + 9 – 6x + y2) = (3x + 4y – 1)2
25x2 – 150x + 25y2 + 225 = 9x2+ 16y2 + 1 + 24xy – 8y – 6x
=> 16x2 + 9y2 – 24xy – 144x + 8y + 224 = 0
Hence, the equation of the parabola is 16x2 + 9y2 – 24xy – 144x + 8y + 224 = 0
(ii) Focus is (1, 1) and the directrix is x + y + 1 = 0
Solution:
Given that, focus is (1, 1) and the directrix is x + y + 1 = 0
Let us assume P (x, y) be any point on the parabola.
So, first we draw PM perpendicular to x + y + 1 = 0.
Then,
SP = PM
SP2 = PM2
(x – 1)2 + (y – 1)2 = 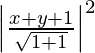
(x – 1)2 + (y – 1)2 = 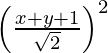
2 (x2 + 1 – 2x + y2 + 1 – 2y) = x2 + y2 + 1 + 2xy + 2y + 2x
(2x2 + 2 – 4x + 2 y2 + 2 – 4y) = x2 + y2 + 1 + 2xy + 2y + 2x
=> x2 + y2 – 2xy – 6x – 6y + 3 = 0
Hence, the equation of the parabola is x2 + y2 – 2xy – 6x – 6y + 3 = 0
(iii) Focus is (0, 0) and the directrix 2x − y − 1 = 0
Solution:
Given that focus is (0, 0) and the directrix 2x − y − 1 = 0
Let us assume P (x, y) be any point on the parabola.
So, the first we draw PM perpendicular to 2x − y − 1 = 0.
Then,
SP = PM
SP2 = PM2
(x – 0)2 + (y – 0)2 = 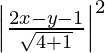
x2 + y2 = 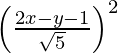
5x2 + 5 y2 = 4x2 + y2 + 1 – 4xy + 2y – 4x
=> x2 + 4y2 + 4xy – 2y + 4x – 1 = 0
Hence, the equation of the parabola is x2 + 4y2 + 4xy – 2y + 4x – 1 = 0
(iv) Focus is (2, 3) and the directrix x − 4y + 3 = 0.
Solution:
Given that focus is (2, 3) and the directrix x − 4y + 3 = 0
Let us assume P (x, y) be any point on the parabola.
So, the first we draw PM perpendicular to x − 4y + 3 = 0.
Then,
SP = PM
SP2 = PM2
(x – 2)2 + (y – 3)2 = 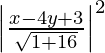
(x – 2)2 + (y – 3)2 = 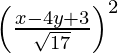
17 (x2 + 4 – 4x + y2 – 6y + 9) = x2 + 16y2 + 9 – 8xy – 24y + 6x
17x2 – 68x – 102y + 17y2 + 13 (17) = x2 + 16y2 + 9 – 8xy – 24y + 6x
=> 16x2 + y2 + 8xy – 74x – 78y + 212 = 0
Hence, the equation of the parabola is 16x2 + y2 + 8xy – 74x – 78y + 212 = 0
Question 2. Find the equation of the parabola whose focus is the point (2, 3) and directrix is the line x − 4y + 3 = 0. Also, find the length of its latus-rectum.
Solution:
Given that, focus is (2, 3) and directrix is the line x − 4y + 3 = 0.
Let us assume P (x, y) be any point on the parabola.
So, first we draw PM perpendicular to x − 4y + 3 = 0.
Then,
SP = PM
SP2 = PM2
(x – 2)2 + (y – 3)2 = 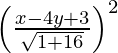
(x – 2)2 + (y – 3)2 = 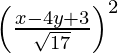
17 (x2 + 4 – 4x + y2 – 6y + 9) = x2 + 16y2 + 9 – 8xy – 24y + 6x
17x2 – 68x + 17y2 – 102y + 9 (17) = x2 + 16y2 + 9 – 8xy – 24y + 6x
16x2 + y2 + 8xy – 74x – 78y + 212 = 0
Length of the latus rectum = 2 (Length of the perpendicular from the focus on the directrix)
= 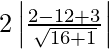
= 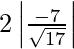
= 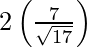
= 4/√17
Hence, the length of its latus-rectum is 4/√17
Question 3. Find the equation of the parabola if
(i) The focus is at (−6, −6) and the vertex is at (−2, 2)
Solution:
Give that, the focus is at (−6, −6) and the vertex is at (−2, 2)
Let us assume (x1, y1) be the coordinates of the point of intersection of the axis and directrix.
So, the slope of the axis of the parabola = 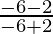 = -8/-4 = 2
= -8/-4 = 2
And the slope of the directrix = -1/2
Let us assume the directrix intersects the axis at point K (r, s), so
(r – 6)/2 = -2, (s – 6)/2 = 2
=> r = 2, s = 10
The equation of the directrix is,
y – 10 = -1/2 (x – 2)
=> 2y + x – 22 = 0
Now, let us assume P (x, y) be any point on the parabola
focus is S (−6, −6).
And the directrix is 2y + x – 22 = 0.
So, first we draw PM perpendicular to 2x + y + 22 = 0.
Then,
SP = PM
SP2 = PM2
(x + 6)2 + (y + 6)2 = 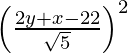
5 (x2 + 12x + 36 + y2 + 12y + 36) = 4y2 + x2 + 484 + 4xy – 88y – 44x
4x2 + y2 – 4xy + 104x + 148y – 124 = 0
=> (2x – y)2 – 4 (26x + 37y – 31) = 0
Hence, the equation of the parabola is (2x – y)2 – 4 (26x + 37y – 31) = 0
(ii) The focus is at (0, −3) and the vertex is at (0, 0)
Solution:
Given that the focus is at (0, −3) and the vertex is at (0, 0)
Let us assume (x1, y1) be the coordinates of the point of intersection of the axis and directrix.
Thus, the slope of the axis of the parabola cannot be defined.
So, the slope of the directrix = 0
Let us assume the directrix intersect the axis at K (r, s).
(r + 0)/2 = 0, (s – 3)/2 = 0
=> r = 0, s = 3
So, the equation of directrix is y = 3
Let us assume P (x, y) be any point on the parabola
With focus is S (0, −3) and the directrix is y = 3.
So, first we draw PM perpendicular to y = 3.
Then,
SP = PM
SP2 = PM2
(x – 0)2 + (y + 3)2 = 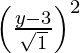
x2 + y2 + 6y + 9 = y2 – 6y + 9
=> x2 = -12y
Hence, the equation of the parabola is x2 = -12y
(iii) Focus is at (0, −3) and the vertex is at (−1, −3)
Solution:
Given that, focus is at (0, −3) and the vertex is at (−1, −3)
Let us assume (x1, y1) be the coordinates of the point of intersection of the axis and directrix.
So, the slope of the axis of the parabola is zero and, the slope of the directrix is
(r + 0)/2 = -1, (s – 3)/2 = – 3
=> r = – 2, s = – 3
The equation of the directrix is x + 2 = 0.
Let us assume P (x, y) be any point on the parabola whose focus is S (0, −3) and the directrix is x + 2 = 0.
So, first we draw PM perpendicular to x + 2 = 0
Then,
SP = PM
SP2 = PM2
(x – 0)2 + (y + 3)2 = 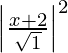
x2 + y2 + 6y + 9 = x2 + 4x + 4
=> y2 + 6y – 4x + 5 = 0
Hence, the equation of the parabola is y2 + 6y – 4x + 5 = 0
(iv) Focus is at (a, 0) and the vertex is at (a’, 0)
Solution:
Given that focus is at (a, 0) and the vertex is at (a’, 0)
Let us assume (x1, y1) be the coordinates of the point of intersection of the axis and directrix.
So, the slope of the axis of the parabola is zero and, the slope of the directrix cannot be defined.
Let us assume the directrix intersect the axis at point K (r, s).
So, (r + a)/2 = a’, (s + 0)/2 = 0
=> r = 2a’ – a, s = 0
The equation of the directrix is x – 2a’ + a = 0
Let us assume P (x, y) be any point on the parabola
with focus is S (a, 0), and the directrix is x – 2a’ + a = 0.
So, first we draw PM perpendicular to x – 2a’ + a = 0
Then,
SP = PM
SP2 = PM2
(x – a)2 + (y – 0)2 = 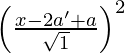
y2 = (x – 2a’ + a)2 – (x – a)2
y2 = x2 + 4a’2 + a2 – 4a’x – 4aa’ + 2ax – x2 – a2 + 2ax
y2 = 4a’2 – 4a’x – 4aa’ + 4ax
=> y2 = -4 (a’ – a) (x – a’)
Hence, the equation of the parabola is y2 = -4 (a’ – a) (x – a’)
(v) Focus is at (0, 0) and vertex is at the intersection of the lines x + y = 1 and x − y = 3.
Solution:
Given that focus is at (0, 0) and vertex is at the intersection of the lines x + y = 1 and x − y = 3.
Let us assume (x1, y1) be the coordinates of the point of intersection of the axis and directrix.
So, the slope of the axis of the parabola =  = -8/-4 = 2
= -8/-4 = 2
And the slope of the directrix = -1/2
Let us assume the directrix intersect the axis at point K (r, s).
so, (r – 6)/2 = -2, (s – 6)/2 = 2
=> r = 2, s = 10
The equation of the directrix is,
y – 10 = -1/2 (x – 2)
=> 2y + x – 22 = 0
Now, let us assume P (x, y) be any point on the parabola
With focus is S (−6, −6) and the directrix is 2y + x – 22 = 0.
So, first we draw PM perpendicular to 2x + y + 22 = 0.
Then,
SP = PM
SP2 = PM2
(x + 6)2 + (y + 6)2 = 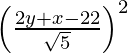
5 (x2 + 12x + 36 + y2 + 12y + 36) = 4y2 + x2 + 484 + 4xy – 88y – 44x
4x2 + y2 – 4xy + 104x + 148y – 124 = 0
=> (2x – y)2 – 4 (26x + 37y – 31) = 0
Hence, the equation of the parabola is (2x – y)2 – 4 (26x + 37y – 31) = 0
Question 4. Find the vertex, focus, axis, directrix, and latus-rectum of the following parabola:
(i) y2 = 8x
Solution:
Given that, y2 = 8x
Now, on comparing the given equation with y2 = 4ax, we get
=> 4a = 8
=> a = 2
So, the vertex = (0, 0)
Focus = (a, 0) = (2, 0)
The equation of the directrix is
x = −a
=> x = −2
Axis = y = 0
Length of the latus rectum = 4a = 4(2) = 8 units
(ii) 4x2 + y = 0
Solution:
Given that,
4x2 + y = 0
=> -y/4 = x2
Now, on comparing the given equation with x2 = -4ay, we get
=> 4a = 1/4
=> a = 1/16
So, the vertex = (0, 0)
Focus = (0, −a) = (0, -1/16)
Equation of the directrix, y = a
=> y = 1/16
Axis = x = 0
Length of the latus rectum = 4a = 4 (1/16) = 1/4 units
(iii) y2 − 4y − 3x + 1 = 0
Solution:
Given that,
y2 − 4y − 3x + 1 = 0
(y – 2)2 – 4 – 3x + 1 = 0
(y – 2)2 = 3 (x + 1)
(y – 2)2 = 3 (x – (-1))
Let us assume Y = y – 2 and X = x + 1.
Then,
Y2 = 3X
Now, on comparing the given equation with Y2 = 4aX, we get
=> 4a = 3
=> a = 3/4
So, the vertex = (X = 0, Y = 0) = (x = -1, y = 2)
Focus = (X = a, Y = 0) = (x + 1 = 3/4, y – 2 = 0) = (x = -1/4, y = 2)
Equation of the directrix: X = −a
i.e. x + 1 = -3/4
=> x = -7/4
Axis = Y = 0
i.e. y – 2 = 0
=> y = 2
Length of the latus rectum = 4a = 4 (3/4) = 3 units
(iv) y2 − 4y + 4x = 0
Solution:
Given that,
y2 − 4y + 4x = 0
(y – 2)2 – 4 + 4x = 0
(y – 2)2 = -4 (x – 1)
Let us assume Y = y – 2 and X = x – 1.
Then,
=> Y2 = – 4X
Now, on comparing the given equation with Y2 = -4aX, we get
=> 4a = 4
=> a = 1
So, the vertex = (X = 0, Y = 0) = (x = 1, y = 2)
Focus = (X = −a, Y = 0) = (x – 1 = – 1, y – 2 = 0) = (x = 0, y = 2)
Equation of the directrix: X = a
i.e. x – 1 = 1
=> x = 2
Axis = Y = 0
i.e. y – 2 = 0
=> y = 2
Length of the latus rectum = 4a = 4 (1) = 4 units
(v) y2 + 4x + 4y − 3 = 0
Solution:
Given that
y2 + 4y + 4x −3 = 0
(y + 2)2 – 4 + 4x – 3 = 0
(y + 2)2 = – 4 (x – 7/4)
Let us assume Y = y + 2 and X = x – 7/4
Then, Y2 = – 4X.
Now, on comparing the given equation with Y2 = -4aX
=> 4a = 4
=> a = 1
So, the Vertex = (X = 0, Y = 0) = (x = 7/4, y = – 2)
Focus = (X = −a, Y = 0) = (x – 7/4 = – 1, y + 2 = 0) = (x = 3/4, y = – 2)
Equation of the directrix: X = a
i.e. x – 7/4 = 1
=> x = 11/4
Axis = Y = 0
i.e. y + 2 = 0
=> y = – 2
Length of the latus rectum = 4a = 4 (1) = 4 units
(vi) y2 = 8x + 8y
Solution:
Given that
y2 = 8x + 8y
(y – 4)2 = 8 (x + 2)
On putting Y = y – 4 and X = x + 2, we get
Y2 = 8X
On comparing the given equation with Y2 = 4aX, we get
=> 4a = 8
=> a = 2
So, the vertex = (X = 0, Y = 0) = (x = – 2, y = 4)
Focus = (X = a, Y = 0) = (x + 2 = 2, y – 4 = 0) = (x = 0, y = 4)
Equation of the directrix: X = −a
i.e. x + 2 = – 2
=> x + 4 = 0
Axis = Y = 0
i.e. y – 4 = 0
=> y = 4
Length of the latus rectum = 4a = 4 (2) = 8 units
(vii) 4 (y − 1)2 = − 7 (x − 3)
Solution:
Given that
4(y − 1)2 = − 7 (x − 3)
(y – 1)2 = -7/4 (x – 3)
Let Y = y – 1 and X = x – 3.
Then,
Y2 = -7/4 X
On comparing the given equation with Y2 = – 4aX, we get
=> 4a = 7/4
=> a = 7/16
So, the vertex = (X = 0, Y = 0) = (x = 3, y = 1)
Focus = (X = −a, Y = 0) = (x – 3 = -7/16, y – 1 = 0) = (x = 41/16, y = 1)
Equation of the directrix: X = a
i.e. x – 3 = 7/16
=> x = 55/16
Axis = Y = 0
i.e. y – 1 = 0
=> y = 1
Length of the latus rectum = 4a = 4 (7/16) = 7/4 units
(viii) y2 = 5x − 4y − 9
Solution:
Given that,
y2 = 5x − 4y − 9
y2 + 4y = 5x – 9
(y + 2)2 = 5x – 5
(y + 2)2 = 5 (x – 1)
On putting Y = y + 2 and X = x – 1, we get
Y2 = 5X
On comparing the given equation with Y2 = 4aX, we get
=> 4a = 5
=> a = 5/4
So the vertex = (X = 0, Y = 0) = (x = 1, y = -2)
Focus = (X = a, Y = 0) = (x – 1 = 5/4, y + 2 =0) = (x = 9/4, y = -2)
Equation of the directrix: X = −a
i.e. x – 1 = -5/4
=> x = -1/4
Axis = Y = 0
i.e. y + 2 = 0
=> y = – 2
Length of the latus rectum = 4a = 4 (5/4) = 5 units
(ix) x2 + y = 6x − 14
Solution:
Given that
x2 = 6x − y − 14
(x – 3)2 = -y – 14 + 9
(x – 3)2 = -y – 5
(x – 3)2 = – (y + 5)
Let us assume Y = y + 5 and X = x – 3.
Then,
X2 = – Y
On comparing the given equation with X2 = – 4aY, we get
=> 4a = 1
=> a = 1/4
So, the vertex = (X = 0, Y = 0) = (x = 3, y = – 5)
Focus = (X = 0, Y = −a) = (x – 3 = 0, y + 5 = -1/4) = (x = 3, y = -21/4)
Equation of the directrix: Y = a
i.e. y + 5 = 1/4
=> y = -19/4
Axis = X = 0
i.e. x – 3 = 0
=> x = 3
Length of the latus rectum = 4a = 4 (1/4) = 1 units
Question 5. For the parabola, y2 = 4px find the extremities of a double ordinate of length 8p. Prove that the lines from the vertex to its extremities are at right angles.
Solution:
Given that the equation of the parabola is y2 = 4px.
Let us assume PQ be the double coordinate of length 8p of the parabola and let A be the vertex of parabola.
y2 = 4px
Then,
PR = RQ = 4p
Let AR = x1
So, the coordinates of P and Q are (x1 , 4p) and (x1, -4p)
Now, P lies on y2 = 4px.
So, (4p)2 = 4p x1
=> x1 = 4p
So, the coordinates of P is (4p, 4p) and Q is (4p, -4p)
The coordinates of A are (0, 0).
So, m1 = Slope of AP = 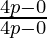 = 4p/4p = 1
= 4p/4p = 1
And, m2 = Slope of AQ = 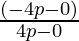 = -4p/4p = -1
= -4p/4p = -1
Now,
m1 m2 = – 1
Thus, AP is perpendicular to AQ.
Hence proved.
Question 6. Find the area of the triangle formed by the lines joining the vertex of the parabola x2 = 12y to the ends of its latus rectum.
Solution:
Given that the equation of the parabola is x2 = 12y.
Now on comparing the given equation with x2 = 4ay, we get
=> 4a = 12
=> a = 3
So, the coordinates of focus are (0, 3).
Now two points lie on the parabola.
=> x2 = 12 (3)
=> x2 = 36
=> x = ±6
Therefore, the points are P (6, 3) and Q (-6, 3).
Distance PQ = 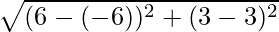
= 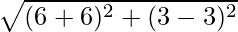
= 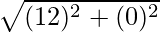
= 12
Area = (PQ) (3) (1/2)
= (12) (3) (1/2)
= 18 sq. units
Therefore, the area of the triangle formed by the lines joining the vertex of the given parabola to the ends of its latus rectum is 18 sq. units.
Question 7. Find the coordinates of the point of intersection of the axis and the directrix of the parabola whose focus is (3, 3) and directrix is 3x − 4y = 2. Find also the length of the latus-rectum.
Solution:
Given that the equation of the directrix is 3x − 4y = 2.
So, the slope of the directrix = -3/-4 = 3/4
Axis is perpendicular to the directrix.
so, the lope of the axis = -4/3
Now, the focus lies on the axis of the parabola.
So, the equation of the axis is
=> y – 3 = (-4/3) (x – 3)
=> 3y – 9 = -4x + 12
=> 3y + 4x – 21 = 0
On solving equations (1) and (2), we get
x = 18/5, y = 11/5
So, the intersection point of the axis and directrix is (18/5, 11/5).
Ad the length of the latus rectum = 2 (Length of the perpendicular from the focus on the directrix)
= 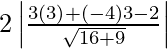
= 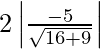
= 2
Question 8. At what point of the parabola x2 = 9y is the abscissa three times that of coordinate?
Solution:
We have,
=> x2 = 9y
Now by putting x = 3y in the given equation of the parabola, we get
=> 9y2 = 9y
=> 9y (y – 1) = 0
=> y = 0, 1
At y = 0, x = 0.
And also at y = 1, x = 3.
Therefore, at (1, 3), the abscissa is three times that of the coordinate.
Question 9. Find the equation of a parabola with vertex at the origin, the axis along the x-axis, and passing through (2, 3).
Solution:
Let us consider the equation of the required parabola be,
=> y2 = 4ax
Since it passes through (2, 3), we get,
=> 9 = 4a (2)
=> 8a = 9
=> a = 9/8
So, the equation is y2 = 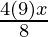
i.e. 2y2 = 9x
Let us assume the equation of the required parabola be y2 = -4ax.
Since the above equation passes through (2, 3), we get
=> 9 = – 4a (2)
=> 8a = -9
=> a = -9/8
Hence, the equation is,
=> y2 = 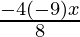
=> 2y2 = 9x
Hence, in either case, the required equation of the parabola is 2y2 = 9x.
Question 10. Find the equation of a parabola with vertex at the origin and the directrix, y = 2.
Solution:
Given that, vertex is (0, 2) and the directrix is y = 2.
Let us assume (x1, y1) be the coordinates of the point of intersection of the axis and directrix.
=> (x1, y1) = (0, 2)
Let us assume the focus be (x2, y2).
Now,
(x2 + 0)/2 = 0 and (y2 + 2)/2 = 0
=> x2 = 0 and y2 = -2
The coordinates of focus are (0, -2).
First we draw PM perpendicular to y = 2.
Then, we have:
SP = PM
SP2 = PM2
(x – 0)2 + (y + 2)2 = 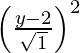
(x – 0)2 + (y + 2)2 = (y – 2)2
x2 + y2 + 4 + 4y = y2 + 4 – 4y
x2 = -4y – 4y
=> x2 = -8y
Hence, the equation of parabola is x2 = -8y.
Share your thoughts in the comments
Please Login to comment...