Frequency Distribution

Frequency Distribution is a tool in statistics that helps us organize the data and also helps us reach meaningful conclusions. Frequency Distribution tells us how often any specific values occur in the dataset. To understand the data easily, we categorize the data into class intervals. The number of items occurring in the specific range or class interval is shown under Frequency against that particular class range to which the item belongs. These distributions allow us to get insights from any data, see the trends, and predict the next values or the direction in which the data will go. Frequency Distribution can be defined for any kind of dataset either grouped or ungrouped. Frequency Distribution is in Class 9 and Class 11 syllabus and hence should be studied by respective students.

In this article, we will learn about all the necessary information which is needed to understand the concept of Frequency Distribution in statistics such as various graphs, Frequency Distribution table, and many more.

What is Frequency Distribution in Statistics?

Frequency distributions tell us how frequencies are distributed over the values. That is how many values lie between different intervals. They give us an idea about the range where most of the values fall and the ranges where values are scarce. 

Frequency Distribution Definition

A frequency distribution is an overview of all values of some variable and the number of times they occur.

Frequency Distribution Graphs

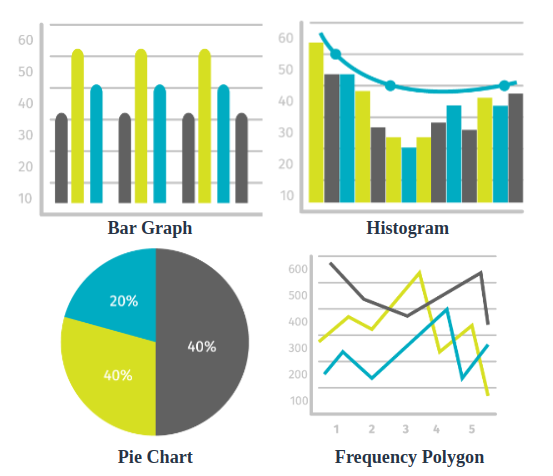
To represent the Frequency Distribution, there are various methods such as Histogram, Bar Graph, Frequency Polygon, and Pie Chart. A brief description of all these graphs is as follows:

Histograms: Histogram is a graphical representation of distribution that represents the frequency of each interval of continuous data generally using bars of equal width. 

Bar Graph: Bar Graph is also a graphical representation of distribution that represents the frequency of each interval using bars of equal width. It can also represent discrete data, unlike a histogram.

Frequency Polygon: A frequency Polygon is a type of graphical representation similar to a histogram but instead of using bars it uses a line to connect the midpoints of the frequencies of the class. It helps us to compare the various different datasets.

Pie Charts: A pie chart is a circular graph that represents the pieces of data in the form of slices of a circle. Each slice represents the proportional size of the data represented by that slice to the complete data set. Pie charts are commonly used to show the relative sizes of different parts of a whole.

Frequency Distribution Table

A frequency distribution table is a way to organize and present data in a tabular form which helps us summarize the large dataset into a concise table. In the frequency distribution table, there are two columns one representing the data either in the form of a range or an individual data set and the other column shows the frequency of each interval or individual. For example, let’s say we have a dataset of students’ test scores in a class.

Test Score	Frequency
0-20	6
20-40	12
40-60	22
60-80	15
80-100	5

How to Make a Frequency Distribution Table?

To make the Frequency Distribution Table, follow these steps:

Step 1: Analyze the ungrouped data given and decide what kind of Frequency Distribution Table is needed – grouped, relative, or cumulative.

Step 2: For a grouped distribution table, decide on the Class Intervals for the observations or, for an ungrouped distribution table, list the unique observations.

Step 3: Count the frequencies of each class or observation.

Step 4: Calculate the relative or cumulative frequency for a grouped distribution table if necessary.

Types of Frequency Distribution Table

Based on the analysis and categorization of the data, there are two types of Frequency Distribution Tables i.e.,

• Grouped Frequency Distribution Table
• Ungrouped Frequency Distribution Table

Let’s learn about these two types in detail.

Grouped Frequency Distribution Table

A grouped frequency distribution table is a table that organizes any given data into intervals or groups, known as class intervals and displays the frequency or number of observations that fall within each interval. 

For example, we can consider the table of the number of cattle owned by families in a town.

Number of Cattle	Number of Families
10 – 20	5
20 – 30	12
30 – 40	8
40 – 50	15
50 – 60	20

In the above table, we can see there are two columns. The first column represents the number of cattle and the second column represents the number of families who own the associate number of cattle. As the first column is grouped with a certain interval length, thus this table is an example of Grouped Frequency Distribution.

Ungrouped Frequency Distribution Table

An ungrouped frequency distribution table is a statistical table that organizes individual data values along with their corresponding frequencies instead of groups or class intervals. For example, consider the number of vowels in any given paragraph.

Vowel	Frequency
a	7
e	10
i	7
o	6
u	3

In the above table, we can the two columns representing a list of vowels and their frequency in any given paragraph. As the first column is a list of some individual elements, thus this table is an example of Ungrouped Frequency Distribution.

Types of Frequency Distribution

There are four types of frequency distributions:

• Grouped Frequency Distribution
• Ungrouped Frequency Distribution
• Relative Frequency Distribution
• Cumulative Frequency Distribution

Grouped Frequency Distribution

In Grouped Frequency Distribution observations are divided between different intervals known as class intervals and then their frequencies are counted for each class interval. This Frequency Distribution is used mostly when the data set is very large.

Example: Make the Frequency Distribution Table for the ungrouped data given as follows:

23, 27, 21, 14, 43, 37, 38, 41, 55, 11, 35, 15, 21, 24, 57, 35, 29, 10, 39, 42, 27, 17, 45, 52, 31, 36, 39, 38, 43, 46, 32, 37, 25

Solution:

As there are observations in between 10 and 57, we can choose class intervals as 10-20, 20-30, 30-40, 40-50, and 50-60. In these class intervals all the observations are covered and for each interval there are different frequency which we can count for each interval. Thus the Frequency Distribution Table for the given data is as follows:

Class Interval	Frequency
10 – 20	5
20 – 30	8
30 – 40	12
40 – 50	6
50 – 60	3

Ungrouped Frequency Distribution

In Ungrouped Frequency Distribution, all distinct observations are mentioned and counted individually. This Frequency Distribution is often used when the given dataset is small.

Example: Make the Frequency Distribution Table for the ungrouped data given as follows:

10, 20, 15, 25, 30, 10, 15, 10, 25, 20, 15, 10, 30, 25

Solution:

As unique observations in the given data are only 10, 15, 20, 25, and 30 with each having a different frequency. Thus the Frequency Distribution Table of the given data is as follows:

Value	Frequency
10	4
15	3
20	2
25	3
30	2

Relative Frequency Distribution

This distribution displays the proportion or percentage of observations in each interval or class. It is useful for comparing different data sets or for analyzing the distribution of data within a set.

and Relative Frequency is given by

Relative Frequency = Frequency of the Event/Total Number of Events

Example: Make the Relative Frequency Distribution Table for the following data:

Score Range	0-20	21-40	41-60	61-80	81-100
Frequency	5	10	20	10	5

Solution:

To Create the Relative Frequency Distribution table, we need to calculate Relative Frequency for each class interval. Thus Relative Frequency Distribution table is given as follows:

Score Range	Frequency	Relative Frequency
0-20	5	5/50 = 0.10
21-40	10	10/50 = 0.20
41-60	20	20/50 = 0.40
61-80	10	10/50 = 0.20
81-100	5	5/50 = 0.10
Total	50	1.00

Cumulative Frequency Distribution

Cumulative frequency is defined as the sum of all the frequencies in the previous values or intervals up to the current one. The frequency distributions which represent the frequency distributions using cumulative frequencies are called cumulative frequency distributions. There are two types of cumulative frequency distributions: 

• Less than type: We sum all the frequencies before the current interval.
• More than type: We sum all the frequencies after the current interval.

Let’s see how to represent a cumulative frequency distribution through an example, 

Example: The table below gives the values of runs scored by Virat Kohli in the last 25 T-20 matches. Represent the data in the form of less-than-type cumulative frequency distribution: 

45	34	50	75	22
56	63	70	49	33
0	8	14	39	86
92	88	70	56	50
57	45	42	12	39

Solution: 

Since there are a lot of distinct values, we’ll express this in the form of grouped distributions with intervals like 0-10, 10-20 and so. First let’s represent the data in the form of grouped frequency distribution. 

Runs	Frequency
0-10	2
10-20	2
20-30	1
30-40	4
40-50	4
50-60	5
60-70	1
70-80	3
80-90	2
90-100	1

Now we will convert this frequency distribution into cumulative frequency distribution by summing up the values of current interval and all the previous intervals. 

Runs scored by Virat Kohli	Cumulative Frequency
Less than 10	2
Less than 20	4
Less than 30	5
Less than 40	9
Less than 50	13
Less than 60	18
Less than 70	19
Less than 80	22
Less than 90	24
Less than 100	25

This table represents the cumulative frequency distribution of less than type. 

Runs scored by Virat Kohli	Cumulative Frequency
More than 0	25
More than 10	23
More than 20	21
More than 30	20
More than 40	16
More than 50	12
More than 60	7
More than 70	6
More than 80	3
More than 90	1

This table represents the cumulative frequency distribution of more than type.

We can plot both the type of cumulative frequency distribution to make the Cumulative Frequency Curve.

Frequency Distribution Curve

A frequency distribution curve, also known as a frequency curve, is a graphical representation of a data set’s frequency distribution. It is used to visualize the distribution and frequency of values or observations within a dataset. Let’s understand it’s different types based on the shape of it, as follows:

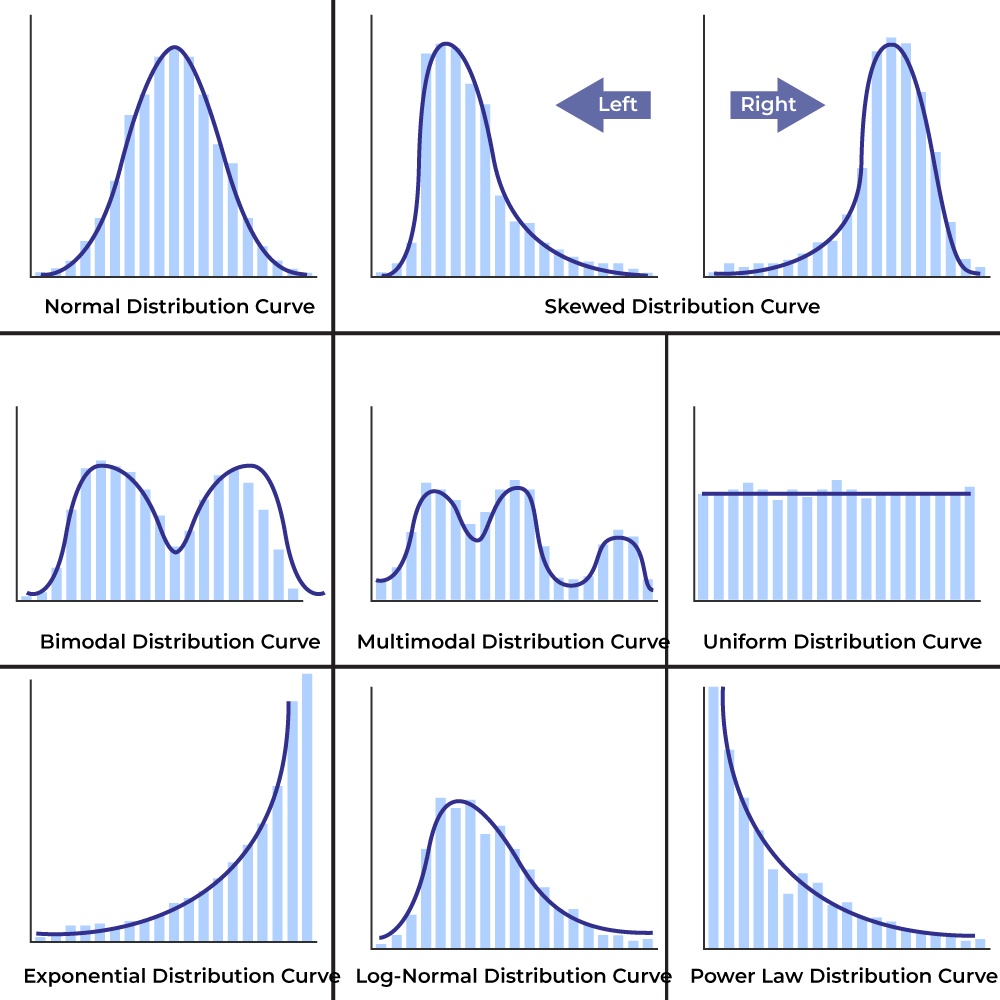
Types of Frequency Distribution Curve

There are various types of Frequency Distribution Curve, some of those are:

Normal Distribution (Gaussian Distribution) Curve: Normal Distribution Curve is the most famous and recognizable curve in all of the Frequency Distribution Curve. It is a symmetric and bell-shaped curve where most of the data is concentrated around the mean and gradually tapers towards the tails.

Skewed Distribution Curve: A distribution is said to be skewed if it is not symmetric. Skewed distributions can be either positively skewed (skewed to the right) or negatively skewed (skewed to the left). In a positively skewed distribution, the tail extends towards higher values, while in a negatively skewed distribution, the tail extends towards lower values.

Bimodal Distribution Curve: A bimodal distribution has two distinct peaks or modes in the frequency distribution. This suggests that the data may arise from two different populations or processes.

Multimodal Distribution Curve: A multimodal distribution has more than two distinct peaks or modes in the frequency distribution.

Uniform Distribution Curve: In a uniform distribution, all values or intervals have roughly the same frequency. This results in a flat, constant distribution across the range of the data.

Exponential Distribution Curve: An exponential distribution is characterized by a rapid drop-off in frequency as values increase just like an exponential function.

Log-Normal Distribution Curve: In a log-normal distribution, the logarithm of the data follows a normal distribution. The resulting distribution is positively skewed and often used to model data that can be multiplicative in nature.

Power Law Distribution Curve: In a power law distribution, the frequency of an event is inversely proportional to its magnitude. This leads to a heavy-tailed distribution where a few extreme events have much higher frequencies than the majority of events.

Frequency Distribution Formula

There are various formulas which can be learned in the context of Frequency Distribution, one such formula is the coefficient of variation. This formula for Frequency Distribution is discussed below in detail.

Coefficient of Variation

We can use mean and standard deviation to describe the dispersion in the values. But sometimes while comparing the two series or frequency distributions becomes a little hard as sometimes both have different units.

For example: Let’s say we have two series, about the heights of students in a class. Now one series measures height in cm and the other one in meters. Ideally, both should have the same dispersion but the out methods of measuring the dispersion are dependent on the units in which we are measuring. This makes such comparisons hard. For dealing with such problems, we define the Coefficient of Variation.

The coefficient of Variation is defined as, 

Where,

• σ represents the standard deviation
•  represents the mean of the observations

Note: The data with greater C.V. is said to be more variable than the other. The series having lesser C.V. is said to be more consistent than the other.

Comparing Two Frequency Distributions with the Same Mean

We have two frequency distributions. Let’s say  are the standard deviation and mean of the first series and  are the standard deviation and mean of the second series. The Coefficeint of Variation(CV) is calculated as follows

C.V of first series = 

C.V of second series = 

We are given that both series have the same mean, i.e.,

So, now C.V. for both series are, 

C.V. of the first series = 

C.V. of the second series = 

Notice that now both series can be compared with the value of standard deviation only. Therefore, we can say that for two series with the same mean, the series with a larger deviation can be considered more variable than the other one.

Frequency Distribution Calculator

The Frequency Distribution Calculator is the calculator, which gives a curve and distribution table as output when entered with ungrouped data. Let’s consider an example of it, how to convert the ungrouped data into a Frequency Distribution Table and Frequency Distribution Curve.

Example: Make a Frequency Distribution Table as well as the curve for the data:

{45, 22, 37, 18, 56, 33, 42, 29, 51, 27, 39, 14, 61, 19, 44, 25, 58, 36, 48, 30, 53, 41, 28, 35, 47, 21, 32, 49, 16, 52, 26, 38, 57, 31, 59, 20, 43, 24, 55, 17, 50, 23, 34, 60, 46, 13, 40, 54, 15, 62}

Answer:

To create the frequency distribution table for given data, let’s arrenge the data in ascending order as follows:

{13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62}

Now, we can count the observations for intervals: 10-20, 20-30, 30-40, 40-50, 50-60 and 60-70.

Interval	Frequency
10 – 20	7
20 – 30	10
30 – 40	10
40 – 50	10
50 – 60	10
60 – 70	3

From this data, we can plot the Frequency Distribution Curve as follows:

Read More,

• Data Handling
• Probability Distribution
• Variance and Standard Deviation

Sample Problems on Frequency Distribution

Problem 1: Suppose we have a series, with a mean of 20 and a variance is 100. Find out the Coefficient of Variation. 

Solution: 

We know the formula for Coefficient of Variation, 

Given mean  = 20 and variance  = 100. 

Substituting the values in the formula, 

Problem 2: Given two series with Coefficients of Variation 70 and 80. The means are 20 and 30. Find the values of standard deviation for both series. 

Solution: 

In this question we need to apply the formula for CV and substitute the given values. 

Standard Deviation of first series. 

Thus, the standard deviation of first series = 14. 

Standard Deviation of second series. 

Thus, the standard deviation of first series = 24. 

Problem 3: Draw the frequency distribution table for the following data: 

2, 3, 1, 4, 2, 2, 3, 1, 4, 4, 4, 2, 2, 2

Solution: 

Since there are only very few distinct values in the series, we will plot the ungrouped frequency distribution. 

Value	Frequency
1	2
2	6
3	2
4	4
Total	14

Problem 4: The table below gives the values of temperature recorded in Hyderabad for 25 days in summer. Represent the data in the form of less-than-type cumulative frequency distribution: 

37	34	36	27	22
25	25	24	26	28
30	31	29	28	30
32	31	28	27	30
30	32	35	34	29

Solution: 

Since there are so many distinct values here, we will use grouped frequency distribution. Let’s say the intervals are 20-25, 25-30, 30-35. Frequency distribution table can be made by counting the number of values lying in these intervals. 

Temperature	Number of Days
20-25	2
25-30	10
30-35	13

This is the grouped frequency distribution table. It can be converted into cumulative frequency distribution by adding the previous values. 

Temperature	Number of Days
Less than 25	2
Less than 30	12
Less than 35	25

FAQs on Frequency Distribution

1. Define Frequency Distribution in Statistics.

A frequency distribution is a table or graph that displays the frequency of various outcomes or values in a sample or population. It shows the number of times each value occurs in the data set.

2. What is the Purpose of a Frequency Distribution?

The purpose of frequency distribution is to organize and summarize the data by showing the frequency of the observations. This helps us identify the patterns in any given set of data.

3. What are the Different Types of Frequency Distributions?

There are four types of frequency distributions that are as follows:

• Grouped Frequency Distribution
• Ungrouped Frequency Distribution
• Relative Frequency Distribution
• Cumulative Frequency Distribution

4. What is an Ungrouped Frequency Distribution?

An ungrouped frequency distribution is a distribution that shows the frequency of each individual value in a data set.

5.  What is a Grouped Frequency Distribution?

A grouped frequency distribution is a distribution that shows the frequency of values within specified intervals or classes.

6.  What is a Relative Frequency Distribution?

A relative frequency distribution is a distribution that shows the proportion or percentage of values within each interval or class.

7. What is a Cumulative Frequency Distribution?

A cumulative frequency distribution is a distribution that shows the number or proportion of values that fall below a certain value or interval.