Use Trigonometric Substitution and Trigonometric Identity to determine the Circumference of a Circle of Radius 3.

When any two-dimensional or three-dimensional plane is being intersected and cut then there are curves obtained, which are known as conic sections. In the case of a cone, there are two identical conical shapes, which are also known as capes. The shape of these conical shapes in the cone depends upon the angle that is opting in as a result of the cut between the plane and the cone. Various shapes can be obtained depending upon the difference in the curve sizes which are circle, hyperbola, ellipse, and parabola we can study these shapes in detail, wherein 

• The ellipse is one of the conic sections, which is formed as a result of the intersection of a plane with the cone at an angle. 
• The circle is considered to be a conic section where the intersection happens parallel to the cone base and it can be considered to be a special type of ellipse. 
• Also, hyperbola formation occurs when the plane is parallel to the cone axis and the intersection happens with both the names of the double cone. 
• Lastly, we obtain a parabola when the intersecting plane cuts the surface of the cone at an angle. 

The following diagram represents the various types of conic sections that are available depending on the difference in the cuts between the intersecting surface and the cone and its necks.

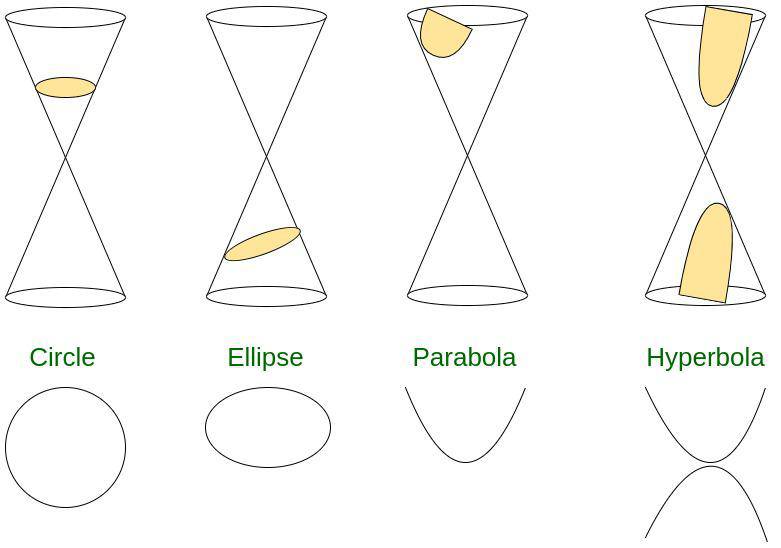
Conic Sections

In this article, we will focus on the conical section of the circle. First, the circle has the following properties,

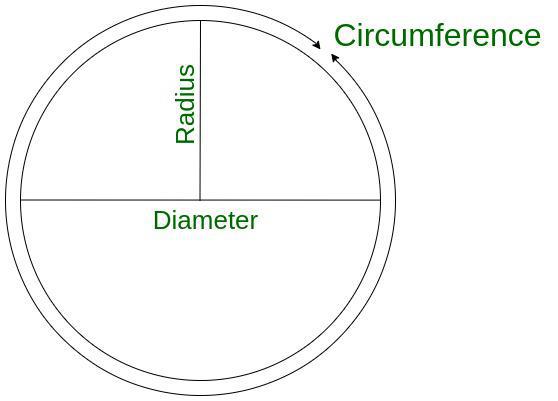
Radius of the Circle

We consider origin to be the centre of the circle. Now, when we start a line segment from this origin and take it to the boundary or edge of the circular object or circular diagram then it is considered to be a Radius. Radius is an important attribute of almost all the geometrical figures that are obtained around us it is also an important concept in the case of spheres, cones with circular bases, cylindrical circular cylindrical bases, etc, therefore, a large number of cylindrical circular figures always tend to be denoted by radius. In other words, if we define the circle as a locus of a point moving in a plane then the distance from the fixed point to the boundary is known as a radius and this distance is always constant in nature that is, the radius in any angle from the origin to the boundary always remains the same. The fixed point of the circle can also be known as the centre of the circle which is an again important attribute of the circle and this point on the line segment together forms the radius therefore, the radius of the circle has two endpoints, one of which is always the origin of the circle. 

Circumference of the Circle

The circle is donated by a complete boundary. If we calculate the length of this boundary, then it gives us the circumference of the circle. The length of the boundary can be calculated by cutting the length at one point and then stretching it so that it becomes a straight line. A large number of infinite points can be arranged on the boundary of the circle and all of these points will be equally distant from the origin. This point which is known as the centre of the circle always holds a constant distance toward any point on the radius of the circle.

Formula

To express the formula for the circumference of the circle we can use the radius(r) and the symbol π.

Circumference of a circle formula = 2πr

Circumference of circle

Diameter of the Circle

The radius of the circle. When multiplied by two gives us a diameter therefore, the diameter of any circle is also constant in nature because the radius is constant in nature and two multiplication of two constants always gives us a constant. Also, the diameter has two endpoints both of which lie on the circumference of the circle and it is also considered to be the maximum distance that can be obtained between any two points on the circumference of the circle. We have 

D = 2R

where,

‘D’ is the diameter and 

‘R’ is the radius of the circle respectively.

Circular Conic Section 

The circle can be extended as a special case of an ellipse, the cutting plane here is parallel to the cone base. This center of the circle is the focus and the radius of the circles is also constant. The value of eccentricity of a circle is always zero that is

e = 0

Now, if we assume that the center of the circle is situated in the Cartesian plane and is marked with the coordinates (h, k) where ‘h’ is the x-coordinate and ‘k’ is the y-coordinate, respectively then the general form of the equation of the circle can be expressed in the following manner. 

(x − h)² + (y − k)² = r²

Here ‘h’ and ‘k’ are the coordinates of the origin, ‘r’ is the radius of the circle which is always constantly nature, and x and y are the coordinates of any other point on the circle.

Use trigonometric substitution and trigonometric identity to determine the circumference of a circle of radius 3.

Solution:

Here,

Radius of the circle (r) = 3

Since, we know, equation of the circle is represented by,

x² + y² = r²

Now, Substituting the values in the above equation,

x² + y² = 3²

y = 

Further differentiating the above equation with respect to x,

Now,

The equation of the circumference of the circle is,

Thus, substituting the values

Further, 

Substitute

x = 3sinθ

dx = 3cosθdθ

Thus at x = 3

Integrating the above equation we will get

Therefore after interacting we get the circumference of the circle with a radius of 3, 

C = 6π

FAQs on Trigonometric Substitution

Question 1: What is trigonometric substitution?

Answer:

Trigonometric functions are substituted in order to compute results for other expressions. This is known as a trigonometric substitution. It is used for the evaluation of regular functions and integrals can also be simplified using substitution methods when the expressions are formed using radicals. Also, the antiderivative can be easily solved before applying the boundaries of integration, and therefore, the process is amplified using trigonometric substitution. 

Question 2: What is a conic section in real life?

Answer:

There are a large number of conic section examples in real life for example, if we consider the Sun as the focus point, then the path or the trajectory of the planets rotating around the sun forms an ellipse. And the other example is the case of parabolic mirrors, which capture the light beam at the focus of a parabola. 

Question 3: What is the formula for the trigonometric equation of a circle?

Answer:

To find the formula for the trigonometric equation of the circle.

We have to,

Assume,

x = acosθ,

y = asinθ

x² + y² = a²cos²θ + a²sin²θ

x² + y² = a²( cos²θ + sin²θ)

x² + y² = a² (by using cos²θ + sin²θ=1)

x² + y² = a²

Question 4: What are trigonometric identities?

Answer:

The trigonometric identities are the expressions that you make use of the trigonometric functions. These trigonometric identities can be considered as the laws in mathematics and therefore, these values of identities hold true for all sets of values provided in them. For instance, trigonometric identities are considered to be appropriate for a right-angled triangle wherein there are six trigonometric ratios that are used to characterize any right-angle triangle. Therefore, irrespective of the side lengths of the right angle triangle, the trigonometric ratio ratios as well as identities are satisfied by all of them. An important feature of the trigonometric identity is that it is made up of using the side length as well as the angles between the sides and then computed.

Question 5: Calculate tan 45º from the unit circle by using the values of sin and cos.

Answer:

Here we have to find the value of tan 45º

As we know that 

tanθ = sinθ/cosθ

So according to the problem

tan 45° = sin 45°/cos 45°

As we know that

sin 45° = 1/√2

cos 45° = 1/√2

Thus,

tan 45° = sin 45°/cos 45°

= {1/√2}/1/√2}

= 1 

Therefore,

tan 45° =  1