Conjugate of Complex Numbers
Last Updated :
25 Apr, 2024
Conjugate of Complex Number is a complex number obtained by changing the sign of the imaginary part. In the world of mathematics, complex numbers are one of the most important discoveries by mathematicians as it helps us solve many real-life problems in various fields such as the study of electromagnetic waves, engineering, and physics.
Complex Numbers are defined as a pair of real numbers and represented as a+ib, where a and b are the real numbers, and i = √(-1) is called iota (an imaginary unit). Some Examples of Complex Numbers include (5 + 3 i), (0 + 7 i), (-4 + 9 i), (1 + 0 i), (0 – i), etc. Now, let’s discuss the conjugate of complex numbers or complex conjugates in detail.
Conjugate of Complex Number Definition
Conjugate of a Complex Number is another complex number whose real parts Re(z) are equal and imaginary parts Im(z) are equal in magnitude but opposite in sign. Conjugate of a complex number z is represented by [Tex]{\overline{z}} [/Tex] while (z & [Tex]{\overline{z}} [/Tex]) together known as complex-conjugate pair because z and [Tex]{\overline{z}} [/Tex] are conjugate to each other.
If z = x + iy is a complex number then the conjugate of z is defined as
[Tex]\bold{\bar{z}= x – iy} [/Tex] = x – iy
From the relation between z and [Tex]{\overline{z}} [/Tex], we can say the conjugate of a complex is obtained by replacing “i” with (-i).
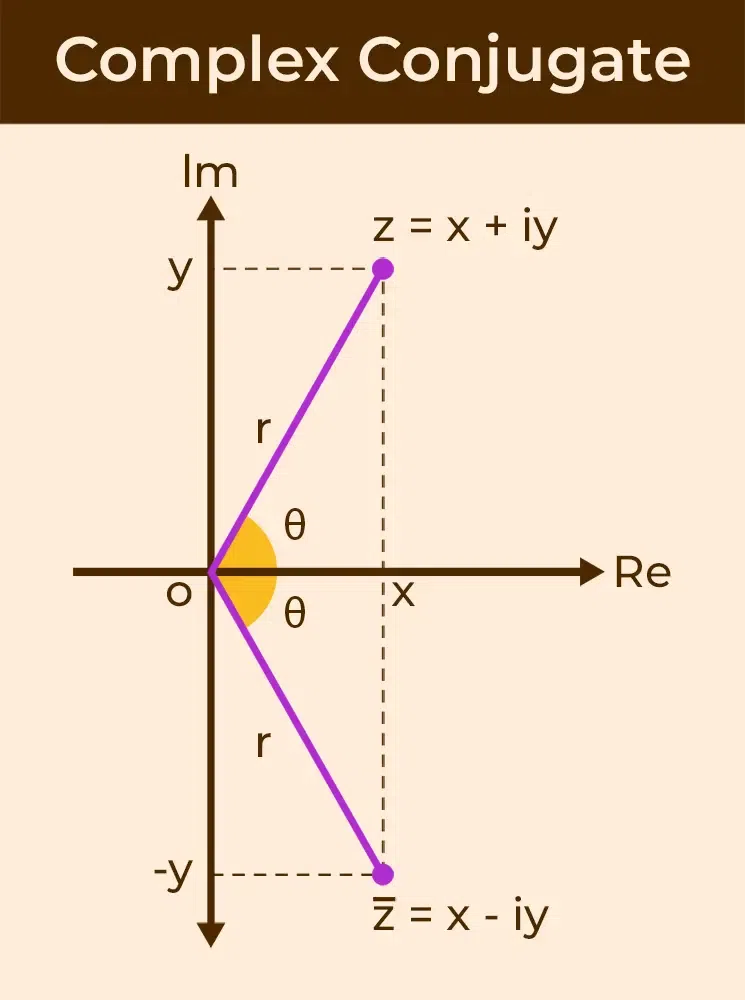
Geometric Interpretation of Complex Conjugate
The geometrical meaning of conjugate of a complex number [Tex]{\overline{z}} [/Tex] is the reflection or mirror image of the complex number z about the real axis (x-axis) in the complex plane or argand plane, which is shown in the following figure:
Complex Conjugate of a Matrix
To calculate the complex conjugate of a matrix, we just need to calculate the complex conjugate of each individual element of the matrix.
For example, [Tex] A = \begin{bmatrix} c&x+iy\\ p-iq&a+ib\end{bmatrix} [/Tex]
Then conjugate of matrix A is given as
[Tex]\overline{A} = \begin{bmatrix} c&x-iy\\ p+iq&a-ib\end{bmatrix}[/Tex]
Properties of Conjugate
If z, z1, and z2 are complex numbers then they will have the following conjugate properties.
- Conjugate of a purely real complex number is the number itself (z = [Tex]{\overline{z}} [/Tex]) i.e., conjugate of (7 + 0 i) = (7 – 0 i) = 7
- Conjugate of a purely imaginary complex number is negative of that number (z + [Tex]{\overline{z}} [/Tex] = 0) i.e. conjugate of (0 -7 i) = (0 + 7 i) = 7 i
- [Tex]{\overline{({\overline{z}})}} [/Tex] = z
- z + [Tex]{\overline{z}} [/Tex] = 2 Re(z)
- z – [Tex]{\overline{z}} [/Tex] = 2 i . Im(z)
- z [Tex]{\overline{z}} [/Tex] = {Re(z)}2 + {Im(z)}2
- [Tex]{\overline{(z_1 + z_2)}} [/Tex] = [Tex]{\overline{z_1} + {\overline{z_2}}}[/Tex]
- [Tex]{\overline{(z_1 – z_2)}} [/Tex] = [Tex]{\overline{z_1} – {\overline{z_2}}}[/Tex]
- [Tex]{\overline{z_1.z_2}} [/Tex] = [Tex]{\overline{z_1} \times {\overline{z_2}}}[/Tex]
- z = (z1 / z2) then [Tex]{\overline{z}} [/Tex] = [Tex]{\overline{z₁}} [/Tex] / [Tex]{\overline{z₂}} [/Tex]; z2 ≠ 0
Note: In order to find out the conjugate of a complex number that complex number must be in its standard form that is Z = (x + i y). If the complex number is not in its standard form then it has to be converted into its standard form before finding its complex conjugate.
Multiplication of Complex Conjugate
The multiplication of complex conjugate is given below:
Let a+ib be a complex number then its conjugate will be a – ib.
Hence, the product of the complex conjugate pair is given as (a + ib)(a – ib) = a2 – i2b2 = a2 + b2
Complex Conjugate Root Theorem
According to Complex Conjugate Root Theorem, if p(x) is a polynomial in which coefficients are real numbers and its root is a + ib then the conjugate of the root a – ib will also be the root of the polynomial.
Read More,
Solved Examples on Conjugates of Complex Numbers
Example 1: If z = (5 + 7 i) is a complex number then its conjugate is given by.
Solution:
The conjugate of the complex number is obtained by changing the sign of the imaginary part.
Thus, [Tex]{\overline{z}}[/Tex] = (5 – 7 i).
Example 2: Find the conjugate of the complex number 3 + 4i.
Solution:
The conjugate of the complex number 3 + 4i is the complex number obtained by changing the sign of the imaginary part, i.e., (3 – 4i).
Therefore, the conjugate of 3 + 4i is 3 – 4i.
Example 3: If z = 1 / (4 + 3 i) is a complex number then its conjugate is given by
Solution:
First z has to be converted into its standard form by multiplying the numerator and
denominator with the conjugate of (4 + 3 i)
z = (1 / (4 + 3 i)) × ((4 – 3 i) / (4 – 3 i))
z = (4 – 3 i) / (16 + 9)
z = (4 / 25) – (3 / 25) i
The conjugate of z is [Tex]{\overline{z}}[/Tex] = (4 / 25) + (3 / 25) i
Example 4: If (a + ib) is a complex number which is the complex conjugate of (8 – 3i) then values of a and b are given by
Solution:
Let z = a + i b
[Tex]{\overline{(8 – 3 i)}} [/Tex] = (8 + 3 i)
z = [Tex]{\overline{(8 – 3 i)}}[/Tex]
z = (8 + 3 i)
Two complex numbers are equal only when their corresponding real & imaginary parts are equal
Equating the real and imaginary parts of z & (8 + 3 i)
Re(z) = a = 8
Im(z) = b = 3
Hence 8 & 3 are the respective values of a and b.
Example 5: Find the product of the complex numbers (2 – 3i) and its conjugate.
Solution:
The conjugate of the complex number (2 – 3i) is (2 + 3i).
Required number is (2 – 3i)(2 + 3i) = 4 -6i + 6i -9i2 = 4 + 9 = 13
Therefore, the product of the complex numbers (2 – 3i) and their conjugate is 13.
FAQs on Conjugate of Complex Numbers
What is a Complex Number?
A Number of Form a+ib, where a and b are real numbers are called complex numbers.
What is a Complex Conjugate?
For a complex number z = a + ib, its complex conjugate is given as a – ib.
How do you find the Conjugate of a Complex Number?
The complex conjugate of a complex number is formed by changing the sign of its imaginary part. For a complex number a + bi, the complex conjugate is a – bi.
How do you graph the Conjugate of a Complex number?
To graph the conjugate of a complex number we just need to reflect the complex number with respect to real axis (x-axis).
What is the Relationship between the Conjugate of a Complex Number and its Inverse?
The relation between the conjugate of a complex number and its inverse as follows:
[Tex]\bold{z^{-1} = \frac{\overline{z}}{|z|}}[/Tex]
Where,|z| is the modulus of complex number.
What is a Complex Conjugate Pair?
Complex number z and its complex conjugate [Tex]\bar{z}[/Tex] are together called complex conjugate pair.
Share your thoughts in the comments
Please Login to comment...