Question 1: How many different words, each containing 2 vowels and 3 consonants can be formed with 5 vowels and 17 consonants.
Solution:
Given, word contains 2 vowels and 3 consonants.
So, we need to choose 2 vowels out of 5 vowels and 3 consonants out of 17 consonants.
This can be done in 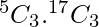 ways.
ways.
Also, we need number of different words, we can arrange 5 letter word in 5! ways.
Therefore, Total number of ways = 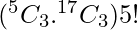
⇒ 6800 × 120 = 816000
Question 2: There are 10 persons named P1,P2,P3….P10 out of 10 persons, 5 persons are to be arranged in a line such that in each arrangement P1 must occur whereas P4 and P5 do not occur. Find the number of such possible arrangements.
Solution:
Given, we need to arrange 5 persons out of 10 persons such that in each arrangements P1 must occur whereas P4 and P5 do not occur.
Here, we Should choose P1 every time, so now, we choose 4 persons out of 9 persons.
From that 9 persons, we don’t need to choose P4 and P5, so This can be done in  ways.
ways.
Therefore, number of selections = 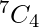
And, 5 persons can be arranged in 5! ways. so,
Total number of ways = 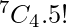
⇒ 4200.
Therefore, number of such possible arrangements is 4200.
Question 3: How many words, with or without meaning can be formed from the letters of the word “MONDAY” assuming that no letter is repeated. if
(i) 4 letters are used at a time.
Solution:
Given, six letter word “MONDAY”.
4 letters are used at a time out of 6 letters. this can be done in 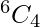 ways.
ways.
These four letters can be arranged in 4! ways.
Therefore, total number of ways = 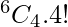
⇒ 360.
(ii) All letters are used at a time.
Solution:
Given, six letter word “MONDAY”.
6 letters are used at a time out of 6 letters. this can be done in 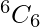 ways.
ways.
These 6 letters can be arranged in 6! ways.
Therefore, Total number of ways = 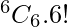
⇒ 1 × 720 = 720
(iii) All letters are used but first letter is a vowel.
Solution:
Given, six letter word “MONDAY”.
All letters are used at a time but first letter is Vowel,
number of vowels in word “MONDAY” is 2. So first we choose one vowel from these two in 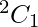 ways.
ways.
The remaining 5 letters out of 5 letters. This can be done in 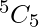 ways.
ways.
Number of arrangements can be done for these 5 letters are 5!.
Therefore, total number of ways = 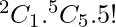
⇒ 2\times1\times120=240.
Question 4: Find the number of permutations of n distinct things taken r together, in which 3 particular things must occur together.
Solution:
Given, Number of permutations of n distinct things taking r together and 3 particular things are already selected.
So, now number of ways of choosing (r – 3) things from remaining (n – 3) things is,
This can be done in 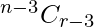 ways.
ways.
We need to find the number of permutations, there are total (r – 2) things considering 3 particular things as single thing.
These can be arranged in (r – 2)! ways.
Internally, 3 particular things can be arranged in 3! ways.
Therefore, Total number of permutations = 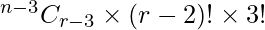
Question 5: How many words of each 3 vowels and 2 consonants can be formed from the letters of the word INVOLUTE?
Solution:
Given word is “INVOLUTE”.
Number of vowels and consonants in the word are 4 and 4 respectively.
Number of ways in choosing 3 vowels out of 4 and 2 consonants out of 4 is 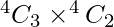
These five letters can be arranged in 5! ways.
Therefore, Total number of words formed = 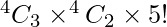
⇒ 4 × 6 × 120 = 2880
Question 6: Find the number of permutations of n different things taken r at a time such that two specified things occur together?
Solution:
Given, number of permutations of n different things taken r at a time and two specified things occur together.
So, we now choose (r – 2) things from the remaining (n – 2) things.
This can be done in 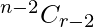 ways.
ways.
We need to find the number of permutations, there are total (r – 1) things considering 2 specific things as single thing.
These can be arranged in (r – 1)! ways.
Internally, 2 particular things can be arranged in 2! ways.
Therefore, Total number of permutations = 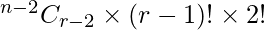
⇒ 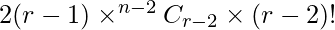
⇒ 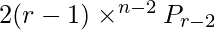
Question 7: Find the number of ways in which: (a) a selection (b) an arrangement, of four letters can be made from the letters of the word ‘PROPORTION’.
Solution:
Given word is ‘PROPORTION’
there are 10 letters in this word and mainly ‘OOO’, ‘PP’, ‘RR’, ‘I’, ‘T’, ‘N’.
(a) Here we need to select 4 letters out of 10 letters. but we need to consider some cases.
- 3 alike letters and 1 distinct letter
- 2 alike letters and 2 distinct letters
- 2 alike letters of I kind and 2 alike letters of other kind.
- all distinct letters.
lets consider,
case-1: 3 alike and 1 distinct
here we find that only one 3 alike letter in the word (‘OOO’).
So, choosing 1 distinct letter from remaining 5 distinct letters is 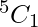
⇒ 5 ways.
case-2: 2 alike letters and 2 distinct letters.
Here, we find that 3 chars have 2 alike letters , number of ways in choosing 1 letters out of 3 is 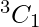
And number of ways of choosing 2 distinct letters from remaining 5 letters is 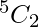
⇒ 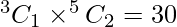 ways.
ways.
case-3 : 2 alike letters of I kind and 2 alike letters of other kind.
Here, we find 3 chars have 2 alike letters, number of ways in choosing 2 letters out of 3 is 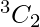
⇒ 3 ways
Case-4: all distinct letters.
Here, we have 6 different letters, number of ways in choosing 4 letters out of 6 is 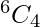
⇒ 15 ways.
Therefore, Total number of ways is sum of number of ways in all cases.
⇒ 5+30+3+15=53 ways.
(b) Here we need to arrange 4 letters out of 10 letters, here cases will be same as selection, but we arrange the given letters in every case.
case-1: Number of ways of selecting 3 alike and 1 distinct letters is 5.
Number of ways in arranging is similar to arranging the n people in n places where r places are same = 
similarly, arrangement of 4 letters where 3 are alike is 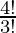
total number of ways are 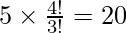
case-2: Number of ways of selecting 2 alike letters and 2 distinct letters is 30 ways.
number ways of arranging them is 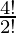
Total number of ways are 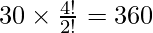
case-3: Number of ways of selecting 2 letters alike and 2 letters alike is 3 ways.
Number of ways in arranging them is 
Total number of ways are 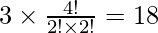
Case-4: Number of ways of selecting 4 distinct letters is 15 ways.
number of ways of arranging them is 4!
Total number of ways are 15 × 4! = 360
considering all cases, Total number of ways are sum of all number of ways of all cases
⇒ 20+360+18+360 = 758 ways.
Question 8: How many words can be formed by taking 4 letters at a time from the letters of word ‘MORADABAD’?
Solution:
Given word is ‘MORADABAD’
There are 10 letters in this word and mainly ‘AAA’, ‘DD’, ‘M’, ‘R’, ‘B’, ‘O’.
(a) Here we need to select 4 letters out of 10 letters. but we need to consider some cases.
- 3 alike letters and 1 distinct letter
- 2 alike letters and 2 distinct letters
- 2 alike letters of I kind and 2 alike letters of other kind.
- all distinct letters.
lets consider,
case-1: 3 alike and 1 distinct
here we find that only one 3 alike letter in the word (‘AAA’).
So, choosing 1 distinct letter from remaining 5 distinct letters is 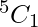
Number of ways of arranging them is 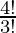
⇒ 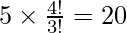 ways.
ways.
case-2: 2 alike letters and 2 distinct letters.
Here, we find that 2 chars have 2 alike letters , number of ways in choosing 1 letters out of 2 is 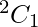
And number of ways of choosing 2 distinct letters from remaining 5 letters is 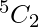
Number of ways of arranging them is 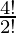
⇒ 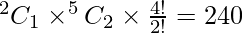 ways.
ways.
case-3 : 2 alike letters of I kind and 2 alike letters of other kind.
Here, we find 2 chars have 2 alike letters, number of ways in choosing 2 letters out of 2 is 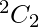
Number of ways of arranging them is 
⇒  ways
ways
Case-4: all distinct letters.
Here, we have 6 different letters, number of ways in choosing 4 letters out of 6 is 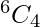
Number of ways of arranging them is 4!
⇒ 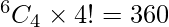 ways.
ways.
Therefore, Total number of ways is sum of number of ways in all cases.
⇒ 20+240+6+360 = 626 ways.
Question 9: A businessman hosts a dinner to 21 guests. He is having 2 round tables which can accommodate 15 and 6 persons each. In how many ways can he arrange the guests?
Solution:
Given, A business man hosts dinners to 21 guests, where 2 round tables accommodate 16 and 6 persons.
So, choosing 15 guests out of 21 to accommodate in one table in 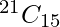 ways.
ways.
Those 15 guests can be arranged in themselves in (15 – 1)! ways. because it is a round table.
So, we need to keep a guest fixed and arrange remaining 14 guests = (15 – 1)! = 14!.
After accommodating 15 guests in one table, accommodating remaining 6 guests out of 6 in another table in 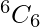 ways.
ways.
Those 6 guests can be arranged themselves in (6 – 1)! = 5! ways.
Total number of ways = 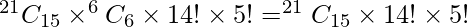
Question 10: Find the number of combinations and permutations of 4 letters taken from the word ‘EXAMINATION’.
Solution:
Given word is ‘EXAMINATION’
There are 10 letters in this word and mainly ‘AA’, ‘NN’, ‘II’, ‘E’, ‘X’, ‘O’,’M’,’T’.
(a) Here we need to select 4 letters out of 10 letters. but we need to consider some cases.
- 2 alike letters and 2 distinct letters
- 2 alike letters of I kind and 2 alike letters of other kind.
- all distinct letters.
lets consider,
case-1: 2 alike letters and 2 distinct letters.
Here, we find that 3 chars have 2 alike letters, number of ways in choosing 1 letters out of 3 is 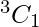
And number of ways of choosing 2 distinct letters from remaining 7 letters is 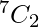
Number of ways of arranging them is 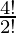
⇒ 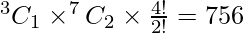 ways.
ways.
case-2 : 2 alike letters of I kind and 2 alike letters of other kind.
Here, we find 3 chars have 2 alike letters, number of ways in choosing 2 letters out of 3 is 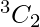
Number of ways of arranging them is 
⇒ 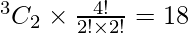 ways
ways
Case-3: all distinct letters.
Here, we have 6 different letters, number of ways in choosing 4 letters out of 8 is 
Number of ways of arranging them is 4!
⇒ 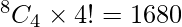 ways.
ways.
Therefore, Total number of ways is sum of number of ways in all cases.
⇒ 756+18+1680 = 2454 ways.
Question 11: A tea party is arranged for 16 persons along two sides of a long table with 8 chairs on each side. Four persons wish to sit on one particular side and two on another side. In how many ways can they be seated?
Solution:
Given, A tea party is arranged 16 persons along two sides of long table with 8 chairs on each side.
Let two sides be side A, side B.
Also, 4 persons wish to sit on side A, and 2 persons on side B.
Remaining seats in side A and side B are 4, 6 respectively.
Now, let we choose 4 persons outs of remaining 10 on side A.
This can be done in 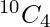 ways.
ways.
Also, choosing 6 persons out of remaining 6 on side B.
This can be done in 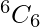 ways.
ways.
Now, 8 persons on each side can be arranged in 8! ways.
Therefore, total number of ways = 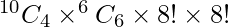
⇒ 
Share your thoughts in the comments
Please Login to comment...