The word “sequence” in English means a collection of some numbers or objects in such a way that it has a first member, a second member, and so on. Sequences can be of anything, for example. – January, February, …. is the sequence of months in a year. Sequences come into use in actual real lives of people every day. Days of a week can also be considered as a sequence. Thus, it becomes essential to study the sequences and find patterns in them so that we can predict the next terms of the sequence and extract information out of them.
Sequences
Let’s consider a sequence: 2,4,6,8 and so on. The various numbers occurring in it are called its terms. They are denoted by a1, a2, a3 … an. The subscripts denote the nth term. The nth term of the sequence is also called the general term of the sequence because we can derive every other term from it by putting different values of n. Here in this case,
a1 = 2, a2 = 4, a3 = 6 and so on…
A sequence with a finite number of terms is called a finite sequence and similarly, a sequence with an infinite number of terms is called an infinite sequence.
A sequence can be regarded as a function whose domain is the set of natural numbers or some subset of it. Sometimes, we use the functional notation a(n) for an.
Series
For a given sequence a1, a2, a3 … an. The expression given below is called a series. A series can be infinite or finite depending upon the number of terms its sequence has. ∑ is the common notation used to denote the series. This indicates the summation involved.
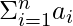 = a1 + a2+ a3 +… an
= a1 + a2+ a3 +… an
These concepts give rise to the sequences known as arithmetic progression and geometric progression.
Arithmetic Progression (A.P)
Consider a sequence 1, 3, 5, 7, ….. Notice that in this sequence, the difference between successive terms is constant. This means that at each step a constant value is being added to each term of this sequence. A sequence a1, a2, a3 … an can be called an arithmetic progression if an+1 = an + d where n is any natural number. In such a series, a1 is called the first term, and the constant term d is called the common difference of A.P. So, an AP looks like,
a, a + d, a + 2d, a + 3d ….. and so on.
The nth for AP can be defined as,
an = a1 + (n-1)d
Sum of n terms of an AP is given by,
Sn = ![Rendered by QuickLaTeX.com \frac{n}{2}[a + (n-1)d]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-25b2961577dffd737f678a8af7763467_l3.png)
or
Sn = ![Rendered by QuickLaTeX.com \frac{n}{2}[a + l]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-607c225c7add019fcc9d92b765a200a1_l3.png)
Geometric Progression (G.P)
Consider the following sequence, 2, 4, 8, 16 ….. It is clear here, that each term is being multiplied by 2 in this sequence. Such sequences where successive terms are multiplied by a constant number are called geometric progressions. In a more general way, a sequence a1, a2, a3 … an can be called a geometric progression if an+1 = an. r where n is any natural number. In such a series, a1 is called the first term, and the constant term r is called the common ratio of G.P. So, a GP looks like,
a, ar, ar2, arn….. and so on.
The nth for GP can be defined as,
an = a1rn-1
In general, GP can be finite and infinite but in the case of infinite GP, the common ratio must be between 0 and 1, or else the values of GP go up to infinity. Sum of GP consists of two cases:
Let’s denote the Sn are a + ar + ar2 + ….. arn
Case 1: If r = 1, the series collapses to
a, a, a, a … and so on.
Sn = na
Case 2: If r≠1, the series stays the same,
a + ar + ar2 + ….. arn
Sn = 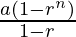
Let’s look at some word problems related to these concepts
Sample Problems
Question 1: A bitcoin stock started at $5. After that, every day it rises by $2. Find the stock price at the end of 16th day.
Answer:
In the above question, each time a constant number is added to the previous term to make a new term. This is an AP.
5, 7, 9, … and so on.
Using the formula for nth term of AP.
an = a1 + (n-1)d
Here a1 denotes the first term and d denotes the common difference. In this case ,
a1 = 5, d = 2 and n = 16
a10 = a1 + (16-1)d
⇒ a10 = 5 + (15)2
⇒ a10 = 5 + 30
⇒ a10 = 35
Thus, the stock prices are at $35.
Question 2: A person planted 3 trees at his son’s birth. After that, on subsequent birthdays he planted 5 more trees every year. Find the number of trees in his backyard when his son is 10years old.
Answer:
In the above question, each time a constant number is added to the previous term to make a new term. This is an AP.
3, 8, 13, … and so on.
Using the formula for nth term of AP.
an = a1 + (n-1)d
Here a1 denotes the first term and d denotes the common difference. In this case,
a1 = 3, d = 5 and n = 10
a10 = a1 + (10-1)d
⇒ a10 = a1 + (9)d
⇒ a10 = 3 + 9(5)
⇒ a10 = 3 + 45
⇒ a10 = 48
Thus, there are 48 trees in his backyard now.
Question 3: English rock band the1975 released a new album in summer, and they opened with 100,000 copies sold within one day. Now the album is topping charts and everyday they sell 20,000 copies more than the previous day. Find the total album sales in a week.
Answer:
In the above question, each time a constant number is added to the previous term to make a new term. This is an AP.
100,000; 120,000; 140,000; … and so on.
Goal is to calculate the sum of the sequence at the end of 10th day.
Using the formula for sum till nth term of AP.
Sn = ![Rendered by QuickLaTeX.com \frac{n}{2}[a + (n-1)d]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-25b2961577dffd737f678a8af7763467_l3.png)
Here a denotes the first term and d denotes the common difference. In this case,
a = 100,000, d = 20,000 and n = 7
Sn = ![Rendered by QuickLaTeX.com \frac{n}{2}[a + (n-1)d]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-25b2961577dffd737f678a8af7763467_l3.png)
⇒S7 = ![Rendered by QuickLaTeX.com \frac{7}{2}[100000 + (7-1)(20000)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e069108ceb2482f1fb7bf6bcc3d2a5b9_l3.png)
⇒S7 = ![Rendered by QuickLaTeX.com \frac{7}{2}[100000 + (6)(20000)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6265ecd00f09f2c9698b2a8eb9dc3064_l3.png)
⇒S7 = ![Rendered by QuickLaTeX.com \frac{7}{2}[100000 + (120000)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-40c9391d735ce9c0af2079e7fbddbb9b_l3.png)
⇒S7 = ![Rendered by QuickLaTeX.com \frac{7}{2}[220000]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-aefa2385b4677af68d7dc4200fb010eb_l3.png)
⇒S7 = 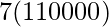
⇒S7 = 770000
Thus, the total album sale is 770,000.
Question 4: The deer population is increasing in Corbett National Park. In year 2015 it was 1000, since then it has been increasing, and it becomes 2 times every year. Find the population in 2021.
Solution.
Here, every year the population becomes 2 times. A constant number is being multiplied to the previous term to get the new term. This is a geometric progression.
1000, 2000 … and so on.
Here a = 1000 and r= 2
Using the formula for nth term of the GP
an = a1rn-1
In 2021, n = 7. Plugging in the values in the formula
an = a1rn-1
⇒an = (1000)(2)(7-1)
⇒an = (1000)(2)6
⇒an = (1000)(64)
⇒an = 64000
There must be 64,000 deer in Corbett National Park now.
Question 5: A person has 2 parents, 4 grandparents, 8 great-grandparents, and so on. Find the number of ancestors in last 10 generations of this family.
Solution.
Here, every year the number becomes 2 times. A constant number is being multiplied to the previous term to get the new term. This is a geometric progression.
2,4 … and so on.
Here a = 2 and r= 2
Using the formula for nth term of the GP
an = a1rn-1
In 2021, n = 10. Plugging in the values in the formula
an = a1rn-1
⇒an = (2)(2)(10-1)
⇒an = (2)(2)9
⇒an = (2)10
⇒an = 64000
There must be 64,000 deer in Corbett National Park now.
Question 6: Insert two numbers between 4 and 256 such that the resulting sequence becomes a GP.
Answer:
Let’s say those two numbers are x and y. The resulting sequence then becomes,
4, x, y, 256
This sequence has four terms and is a GP. Here,
a = 4 and r = ?
Formula for nth term of GP is
an = a1rn-1
4th term is 256,
256 = 4r(4 – 1)
64 = r3
This means that, r = 4
Thus,
x = ar
⇒ x = (4)(4)
⇒ x= 16
y = ar2
⇒ y = 4(4)2
⇒ y = 64
So, the two numbers to be inserted are 16 and 64
Question 7: Number of bacteria in a dish are 100, and they are increasing by double the previous value every hour. Find the number of bacteria in the dish after 6 hours.
Answer:
Here, every year the number becomes 2 times. A constant number is being multiplied to the previous term to get the new term. This is a geometric progression.
100,200, 400 … and so on.
Here a = 100 and r= 2
Using the formula for sum till nth term of the GP
Sn = 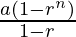
n = 6. Plugging in the values in the formula
Sn = 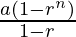
⇒Sn = 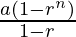
⇒ S6 = 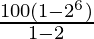
⇒ S6 = 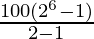
⇒ S6 = 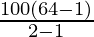
⇒ S6 = 6300
There must be 63,00 bacteria in the dish now.
Share your thoughts in the comments
Please Login to comment...