Trigonometric Functions, often simply called trig functions, are mathematical functions that relate the angles of a right triangle to the ratios of the lengths of its sides. These Trigonometric functions are fundamental in mathematics for units like Calculus and Geometry and have wide-ranging applications in science, engineering, and various other fields.
In this article, we will in detail about trigonometric functions, their domain and range, and other related facts.
What are Trigonometric Functions?
Trigonometric functions are the basic functions used in trigonometry and they are used for solving various types of problems in physics, Astronomy, Probability, and other branches of science. There are six basic trigonometric functions used in Trigonometry which are:
These trigonometric functions are used to represent the relation between the angles and the sides of the triangle and plotting the graph of these functions result in some interesting curves that are used for scientific purposes and represent various real-life incidents.
Trigonometry Functions Definition
Trigonometric functions, often referred to as trig functions, are mathematical functions that establish relationships between the angles and sides of a right triangle. The primary trigonometric functions include sine (sin), cosine (cos), and tangent (tan), but there are also their reciprocal functions: cosecant (csc), secant (sec), and cotangent (cot). Trigonometry formulas are composed of various trigonometric functions.
Six Trigonometric Functions
The Six Trigonometric Functions are listed below.
- Sine Function (sin x)
- Cosine Function (cos x)
- Tangent Function (tan x)
- Cosecant Function (cosec x)
- Secant Function (sec x)
- Cotangent Function (cot x)
Out of these six trigonometric functions, three (sin x, cos x, and tan x) are important functions and the other three (cosec x, sec x, and cot x) are respectively the reciprocal functions of the above function. In this article, we will cover a range of topics like what are trigonometric functions, their formulas, and all 6 trigonometric functions – Sin, Cos, Tan, Cot, Sec, and Cosec in Trigonometry.
The image added below shows a right angle triangle PQR.
-(1).png)
Sine Function
Sine function of an angle is the ratio of perpendicular and the hypotenuse in the right angle triangle. Form the image added above,
- sin θ = Perpendicular/Hypotenuse = PQ/PR
Cos Function
Cos function of an angle is the ratio of base and the hypotenuse in the right angle triangle. Form the image added above,
- cos θ = Base/Hypotenuse = QR/PR
Tan Function
Tan function of an angle is the ratio of perpendicular and the base in the right angle triangle. Form the image added above,
- tan θ = Perpendicular/Base = PQ/QR
Secant, Cosecant, and Cotangent Functions
Secant(sec), Cosecant(cosec), and Cotangent(cot) functions are the reciprocal function of cos, sine, and tan function and there values is calculated as, (from the right-angled triangle PQR added above)
- sec θ = Hypotenuse/Base = PR/PQ
- cosec θ = Hypotenuse/Perpendicular = PR/QR
- cot θ = Base/Perpendicular = QR/PQ
Formula for various trigonometric functions is given with the help of a right angle triangle. Suppose we have a right angle triangle ABC right angled at B then the side opposite to the angle A is called the perpendicular and the side opposite to angle B is called the Base of the triangle and the side opposite to the right angle is the hypotenuse(which is also the largest side of the triangle).
Then the basic trigonometric functions formulas for this right angle triangle is,
- sin θ = Perpendicular/Hypotenuse
- cos θ = Base/Hypotenuse
- tan θ = Perpendicular/Base
- sec θ = Hypotenuse/Base
- cosec θ = Hypotenuse/Perpendicular
- cot θ = Base/Perpendicular
Observing the above formula it is evident that sec θ, cosec θ, and cot θ are simply the reciprocal values of sin θ, cos θ, and tan θ respectively.
Trigonometric Functions Values
Value of trigonometric functions can easily be given using the trigonometry table. These values of the trigonometric functions are very useful in solving the various trigonometric problems. The required trigonometry table is added below:
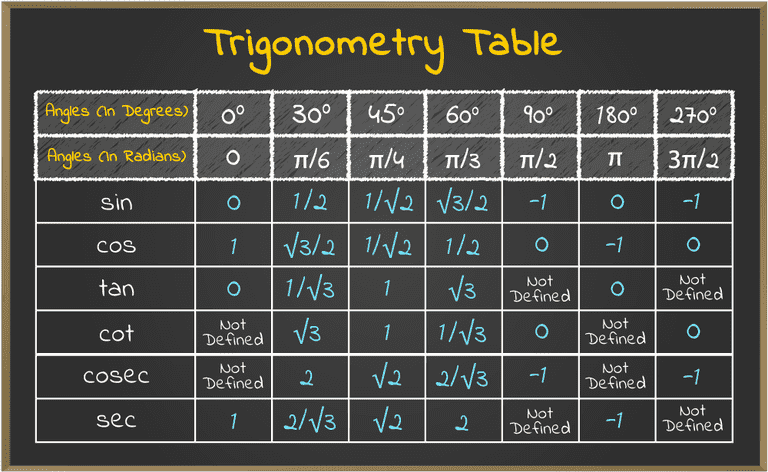
The table added below shows all the values of the important angles from 0 to 180 degrees for all the trigonometric functions.
Trigonometric Functions in Four(4) Quadrants
The trigonometric functions are the periodic functions and their value repeat after a certain interval. Also, not all the trigonometric functions are positive in all the quadrants.
We divide the cartesian space into four quadrants namely, I, II, III and IV quadrants, and the value of the trigonometric functions whether they are positive or negative in each quadrant is given as,
- I Quadrant: All Positive
- II Quadrant: sin θ and cosec θ Positive
- III Quadrant: tan θ and cot θ Positive
- IV Quadrant: cos θ and sec θ Positive
Image explaining the same is added below:
.png)
Graphs of Trigonometric Functions
Trigonometric functions graphs plots the value of the trigonometric functions for different values of the angle(θ). For some the trigonometric functions are bounded as,
- Trigonometric functions sin θ and cos θ are bounded between – 1 and 1 and to their graphs oscillates between -1 and 1 on the y-axis.
- Graph of the trigonometric function tan θ, and cot θ has a range from negative infinity to positive infinity.
- Graph of the trigonometric function sec θ, and cosec θ has a range from negative infinity to positive infinity excluding (-1, 1).
Trigonometric Functions Identities
There are various identities that are related to the trigonometric function these identities link different trigonometric function with each other and are very useful in solving various trigonometric problems. Various trigonometry identities used by us are,
Reciprocal Identities
Reciprocal Identities of the trigonometric functions include,
- cosec θ = 1/sin θ
- sec θ = 1/cos θ
- cot θ = 1/tan θ
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
Pythagorean Identities
Pythagorean Identities of the trigonometric functions include,
- sin2θ + cos2θ = 1
- 1 + tan2θ = sec2θ
- 1 + cot2θ = cosec2θ
Complementary Angles Identities
Complementary Angles Identities of the trigonometric functions include,
- sin (90° – θ) = cos θ
- cos (90° – θ) = sin θ
- tan (90° – θ) = cot θ
- cot ( 90° – θ) = tan θ
- sec (90° – θ) = cosec θ
- cosec (90° – θ) = sec θ
Supplementary Angles Identities
Supplementary Angles Identities of the trigonometric functions include,
- sin (180°- θ) = sinθ
- cos (180°- θ) = -cos θ
- cosec (180°- θ) = cosec θ
- sec (180°- θ)= -sec θ
- tan (180°- θ) = -tan θ
- cot (180°- θ) = -cot θ
Even and Odd Trigonometric Functions
Among the six trigonometric functions Cos and Sec functions are even functions and the rest four function Sin, Tan, Cosec, and Cot are odd function, i.e.
- sin(-x) = -sin x
- cos(-x) = cos x
- tan(-x) = – tan x
- cot(-x) = -cot x
- csc(-x) = -csc x
- sec(-x) = sec x
Periodic Trigonometric Functions
Trigonometric Functions are periodic functions and the period of trigonometric function are added below,
- sin(x+2nπ) = sin x
- cos(x+2nπ) = cos x
- tan(x+nπ) = tan x
- cot(x+nπ) = cot x
- csc(x+2nπ) = csc x
- sec(x+2nπ) = sec x
Domain and Range of Trigonometric Functions
Trigonometric functions are compared to normal functions so the domain and range of the trigonometric functions are comparable to normal function. Suppose we have a trigonometric function f(x) = sin x, then the domain of the function f(x) is all the values of x that the function f(x) can take, and the domain is all possible outcome of the f(x). The domain and range of all the six trigonometric functions are added below,
Trigonometric Function – Domain and Range
Domain and range of the trigonometric function is shown in the table added below,
|
Trigonometric Function
|
Domain
|
Range
|
| sin x |
R |
[-1, +1] |
| cos x |
R |
[-1, +1] |
| tan x |
R – (2n + 1)π/2 |
R |
| cot x |
R – nπ |
R |
| sec x |
R – (2n + 1)π/2 |
(-∞, -1] U [+1, +∞) |
| cosec x |
R – nπ |
(-∞, -1] U [+1, +∞) |
Derivative of Trigonometric Functions
Differentiation of trigonometric function can be easily found and which the slope of that curve for that specific value of the trigonometric functions. The differentiation of all six trigonometric functions are added below:
- d/dx (sin x) = cos x
- d/dx (cos x) = -sin x
- d/dx (tan x) = sec2x
- d/dx (cot x) = -cosec2x
- d/dx (sec x) = sec x tan x
- d/dx (cosec x) = -cosec x cot x
Integration of Trigonometric Functions
As integration of any curve gives the area under the curve, the integration of trigonometric function also give the area under the trigonometric function. The integration of various trigonometric functions are added below.
- ∫ cos x dx = sin x + C
- ∫ sin x dx = -cos x + C
- ∫ tan x dx = log|sec x| + C
- ∫ cot x dx = log|sin x| + C
- ∫ sec x dx = log|sec x + tan x| + C
- ∫ cosec x dx = log|cosec x – cot x| + C
- ∫ sec2x dx = tan x + C
- ∫ cosec2x dx = -cot x + C
- ∫ sec x tan x dx = sec x + C
- ∫ cosec x cot x dx = -cosec x + C
Inverse Trigonometric Functions
Inverse Trigonometric Functions are the inverse of the trigonometric function. Suppose we have a trigonometric function f(x) = sin x, such that sin x = a then f-1 (x) is the inverse of f(x) and is called the inverse trigonometric function and is defined as,
y = sin x
⇒ x = sin-1(y)
Arbitrary values of trigonometric functions are,
- sin-1(-x) = -sin-1x
- cos-1(-x) = π – cos-1x
- tan-1(-x) = -tan-1x
- cosec-1(-x) = -cosec-1x
- sec-1(-x) = π – sec-1x
- cot-1(-x) = π – cot-1x
Inverse Trigonometric Reciprocal Functions
Inverse trigonometric reciprocal functions are added below:
- sin-1x = cosec-11/x
- cos-1x = sec-11/x
- tan-1x = cot-11/x
Inverse Trigonometric Complementary Functions
Inverse trigonometric complementary functions are are the functions that adds up to π/2 and they are,
- sin-1x + cos-1x = π/2
- tan-1x + cot-1x = π/2
- sec-1x + cosec-1x = π/2
Examples on Trigonometric Functions
Example 1: Simplify (cosec2θ – 1) tan²θ
Solution:
= (cosec²θ – 1) tan2θ
= (1 + cot2θ – 1) tan2θ {using cosec²θ – cot2θ = 1}
= cot2θ . tan2θ
= (1/tan2θ) . tan2θ
= 1
Example 2: Simplify (1 – sin2θ) sec2θ = 1
Solution:
= (1 – sin2θ) sec2θ
= cos2θ . sec2θ {using sin²θ + cos2θ = 1}
= cos2θ . (1/cos2θ)
= 1
Example 3: Find the value of cos 75°.
Solution:
= cos 75°
= cos (30° + 45°) {using cos(x+y) = cos(x)cos(y) – sin(x)sin(y)}
= cos30°.cos45° – sin30°.sin45°
= (√3/2) (1/√2) + (1/2) (1/√2)
= √3/2√2 – 1/2√2
= (√3 – 1)/2√2
Example 4: Find the values of cos 45°, sin 60° and tan 30° using trigonometry table.
Solution:
Using Trigonometric Table added above,
- cos 45° = 1/√2
- sin 60° = √3/2
- tan 30° = 1/√3
Practice Problems on Trigonometric Functions
1. Find the value of sin(30 degrees) without using a calculator.
2. Calculate cos(45 degrees) without using a calculator.
3. Determine the exact value of tan(60 degrees) without a calculator.
4. If sin(θ) = 0.6, find the value of θ in degrees, where 0° ≤ θ ≤ 90°.
5. Calculate the value of cos(120 degrees) without a calculator.
6. Find the value of tan(π/4) without using a calculator.
7. Given that cos(θ) = -0.8, find the value of θ in degrees, where 0° ≤ θ ≤ 360°.
Trigonometric Functions-FAQs
What are Trigonometric Functions in Maths?
Trigonometric Functions are the function used in trigonometry these functions gives the relation between, the angles and the sides of the triangle.
What are Six Basic Trigonometric Functions?
The six trigonometric functions are,
- sin x
- cos x
- tan x
- cosec x
- sec x
- cot x
What are Pythagorean Identities of Trigonometric Function?
Pythagorean Identities of Trigonometric Function are,
- sin2θ + cos2θ = 1
- 1 + tan2θ = sec2θ
- 1 + cot2θ = cosec2θ
What are Inverse Trigonometric Functions?
Inverse Trigonometry Functions as the name suggest are the inverse of the trigonometric functions. We can explain this as suppose,
sin x = a
Then inverse of sin function is sin-1 and its value is defined as,
sin-1(a) = x
Similarly, inverse function of all the trigonometric functions can be easily calculated.
What are Applications of Trigonometric Functions?
Trigonometric functions are very useful and they are used in various branches of mathematics, and physics for various purposes. They are used in Coordinate Geometry, Complex Analysis, etc. They are also used in Astronomy, Wave Physics, etc.
What is Domain and Range of Trigonometric Functions?
The Domain of a trigonometric function is the value of θ for which the function has a real value.
Range of a trigonometric Function is the interval in which the value of the trigonometric function exists.
Is it Important to study Trigonometric Functions for Class 11?
Yes, Trigonometric Functions is very important for Class 10 as well as Class 11 Students. As it forms a base to study other units including Calculus and Geometry.
What are 3 Basic Trig Function?
The three basic trig functions are,
- Sine Function (sin x)
- Cosine Function (cos x)
- Tangent Function (tan x)
Share your thoughts in the comments
Please Login to comment...