‘Product‘ mathematically signifies the result obtained when two or more values are multiplied together. For example, 45 is the product of 9 and 5. One must be familiar with the basic operations on sets like Union and Intersection, which are performed on 2 or more sets. Cartesian Product is also one such operation that is performed on two sets, which returns a set of ordered pairs.
In this article, we have covered, ordered pair definition, cartesian product of sets, and others in detail.
What is an Ordered Pair?
An ordered pair has two parts. The first part is called the first component. The second part is called the second component. We write an ordered pair like this: (a, b). The letter ‘a’ is the first component. The letter ‘b’ is the second component. An ordered pair has two things. One thing comes first. The other thing comes second.
Example:
(5, 7) is an ordered pair of integers.
Note: (5, 7) ≠ (7, 5), an ordered pair (a, b) is equal to (x, y) only if a = x and b = y.
Cartesian Product of Sets
When two sets have items in them, A and B, their Cartesian product is all the pairs you can make. One part of the pair comes from set A. The other part comes from set B. We make every possible pair this way. The result is a new set of all these pairs. We write this new set as A×B.
A × B = {(a, b) : a ∈ A and b ∈ B}
Example:
Let A = {1, 2} and B = {4, 5, 6}
A × B = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6)}
Here the first component of every ordered pair is from set A the second component is from set B.
Cartesian Product of two sets can be easily represented in the form of a matrix where both sets are on either axis, as shown in the image below. Cartesian Product of A = {1, 2} and B = {x, y, z}
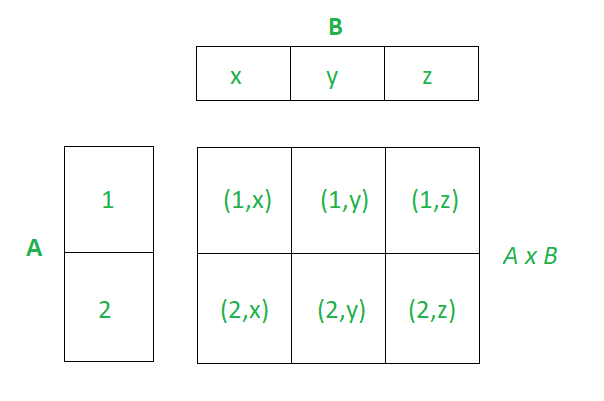
Properties of Cartesian Product
Various properties of cartesian product includes,
1. Cartesian Product is non-commutative: A × B ≠ B × A
Example:
A = {1, 2} , B = {a, b}
A × B = {(1, a), (1, b), (2, a), (2, b)}
B × A = {(a, 1), (b, 1), (b, 1), (b, 2)}
Therefore as A ≠ B we have A × B ≠ B × A
2. A × B = B × A, only if A = B
Proof:
Let A × B = B × A then we have
A ⊆ B and B ⊆ A, it follows that A = B
3. Cardinality of Cartesian Product is defined as number of elements in A × B and is equal to the product of cardinality of both sets i.e.,
|A × B| = |A| × |B|
Proof:
Let a ∈ A then the number of ordered pair (a, b) such that b ∈ B is |B|
Therefore we have |B| choices for b for each a where a ∈ A therefore the number of element in A × B is |A| × |B|
4. A × B = ∅, if either A = ∅ or B = ∅
Proof:
We know |{∅}| = 1
Now we have |A × B| = |{∅}| = 1
As |A × B| = |A| × |B|, we get |A| × |B| = 1
Thus, at least one of |A| or |B| should be equal to 1
Hence, either A = {∅} or B = {∅}
Read More,
Problems on Cartesian Product of Sets
Problem 1: Find the value of x and y given (2x – y, 25) = (15, 2x + y)?
Solution:
As we know from the property of ordered pairs, 2x – y = 15 and 25 = 2x + y.
Solving the linear equations we have x = 10 and y = 5.
Problem 2. Given A = {2, 3, 4 , 5} and B = {4 , 16 , 23}, a ∈ A, b ∈ B, find the set of ordered pairs such that a2 < b?
Solution:
As 22 < 16 and 23, 32 < 16 and 23, 42 < 23
We have the set of ordered pairs such that a2 < b is {(2, 16), (2, 23), (3, 16), (2, 23), (4, 23)}
Problem 3. If A = {9, 10} and B = {3, 4, 6}, find A × B and |A × B|?
Solution:
A × B = {(9, 3), (9, 4), (9, 6), (10, 3), (10, 4), (10, 6)}
|A × B| = |A| * |B| = 2 * 3 = 6
Problem 4. If A × B = {(a, x), (a, y ), (b, x ), (b, y)}, find A and B?
Solution:
We know A is the set of all first components in ordered pairs of A × B and
B is the set of the second component in the ordered pair of A × B.
Therefore A = {a, b} and B = {x, y}
Problem 5. Given A × B has 15 ordered pairs and A has 5 elements, find the number of elements in B?
Solution:
We know |A × B| = |A| * |B|, 15 = 5 * |B|
Therefore B has 15 / 5 = 3 elements.
Practice Problems on Cartesian Product of Sets
Problem 1: Let A = {a, b, c} and B = {1, 2}. Find A × B.
Problem 2: Let A = {} and B = {x, y}. Find A × B.
Problem 3: Let A = {apple, banana} and B = {red, yellow}. Find A × B.
Problem 4: Let A = {1, 2, 3} and B = {3, 4, 5}. Find A × B.
Problem 5: Let A = {cat} and B = {dog}. Find A × B.
FAQs on Cartesian Product of Sets
What is cartesian product of two sets i.e., A×B?
Cartesian product of sets A and B, denoted A×B, is the set of all possible ordered pairs where the first element is from A and the second from B.
Define ordered pair.
An ordered pair is a pair of elements (a, b) in which the order of the elements is significant. This means (a, b) is distinct from (b, a) if a is not equal to b.
What is cartesian product of 3 sets?
Cartesian product of three sets A, B, and C is the set of all possible ordered triples where first element is from A, second from B, and third from C.
Write formula for cartesian product of sets.
Cartesian product of two sets A and B is defined as:
A × B = {(a, b) | a ∈ A and b ∈ B}
For three sets A, B, and C:
A × B × C = {(a, b, c) | a ∈ A, b ∈ B, and c ∈ C}
What is cartesian product of a set and a null set?
Cartesian product of a set A and a null set (∅) is always an empty set (∅), as there are no elements in the null set to form pairs with elements from set A.
Share your thoughts in the comments
Please Login to comment...