Class 11 RD Sharma Solutions- Chapter 22 Brief Review of Cartesian System of Rectangular Coordinates- Exercise 22.1
Last Updated :
10 May, 2021
Question 1. If the line segment joining the points P(x1,y1) and Q(x2,y2) subtends an angle ∅ at the origin O, prove that OP.OQ cos∅ = x1x2 + y1y2.
Solution:
Since, O is the origin, we can get, OP2 = x12 + y12 and OQ2 = x22 + y22
Also, by the distance formula we know distance between two points P and Q is:
PQ2 = (x2 – x1)2 + (y2 – y1)2
Using the cosine formula, in triangle OPQ, we have
PQ2 = OP2 + OQ2 – 2 (OP). (OQ) cos∅
⇒ (x2 – x1)2 + (y2 – y1)2 = x12 + y12 + x22 + y22 – 2 (OP). (OQ) cos∅
⇒ x22 + x12 – 2 x2x1 + y22 + y12 – 2y2y1 = x12 + y12 + x22 + y22 – 2 (OP). (OQ) cos∅
⇒ – 2 (x1x2 + y1y2) = – 2 (OP). (OQ) cos∅
⇒ OP.OQ cos∅ = x1x2 + y1y2
Question 2. The vertices of a triangle ABC are A(0,0), B (2,-1) and C (9,0). Find cos B.
Solution:
Using the cosine formula, we know
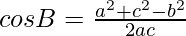
Now, lets assume, a = BC, b = CA and c = AB are the sides of the triangle ABC.
Therefore, the distance between two consecutive points can be calculated as:
a = BC = 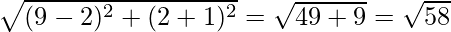
b = CA = 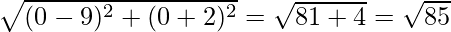
and c = AB = 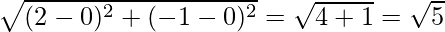
Using the cosine formula,
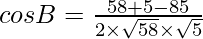
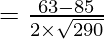
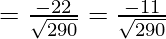
Hence, 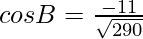
Question. 3 Four points A(6,3), B(-3,5), C(4,-2) and D(x,3x) are given in such a way that 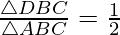 , find x.
, find x.
Solution:
We know the formula that,
area of a triangle = ![Rendered by QuickLaTeX.com \frac{1}{2}[x_1(y_2-y_1) + x_2(y_3-y_2) + x_3(y_3-y_1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-caa3e10ffa442eb1df8a8df78e2a4e0e_l3.png) , so
, so
area of triangle ABC = ![Rendered by QuickLaTeX.com \frac{1}{2}[-3(-2-3x) + 4(3x-5) + x(5+2)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-86cef0271fa667c227853bfb1552c861_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{2}[6+ 9x+ 12x -20 + 5x +2x]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-abff5bb9bc159421d5275d9a1d0ba828_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{2}[28x -14] = 14x - 7](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3a6db441287d56dbdb7d494d4ef7a7dd_l3.png)
Similarly, area of triangle DBC = ![Rendered by QuickLaTeX.com \frac{1}{2}[6(5+2) - 3(-2-3) + 4(3-5)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-45f446ceadf0ac7c0852c7aa4ed0f32d_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{2}[42+15-8]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-77ed13901ad3b990edfde2df4e013a0a_l3.png)
= 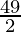
Now, we are given that
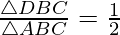
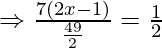
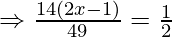
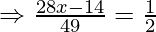

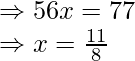
Question. 4 The points A(2,0), B(9,1), C(11,6) and D (4,4) are the vertices of a quadrilateral ABCD. Determine whether ABCD is a rhombus or not.
Solution:
We know the property of a rhombus that the diagonals bisect each other at the right angles. Thus, both the diagonals must have a common mid-point.
Now mid-point of line AC = 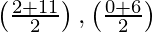 = (13/2, 3)
= (13/2, 3)
and mid-point of line BD = 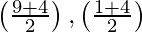 =
= 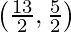
Since, both the lines have different mid-points, we can conclude that the quadrilateral ABCD is not a rhombus.
Question 5. Find the coordinates of the centre of the circle inscribed in a triangle whose vertices are (-36,7), (20,7), and (0,-8).
Solution:
Since, the circle is inscribed in a triangle, the centre of the circle is known as incentre. We know that incentre of a circle (O) inscribed in a triangle is given by the formula:
O = 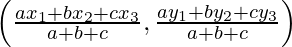 , where a, b, c are length opposite to ∠A, ∠B and ∠C respectively.
, where a, b, c are length opposite to ∠A, ∠B and ∠C respectively.
Therefore, lets say a = BC = 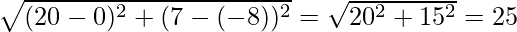
similarly, b = AC = 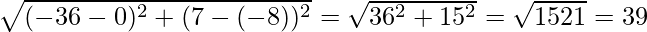
and c = AB = 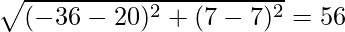
Therefore, the coordinates of the incentre will be:
O = 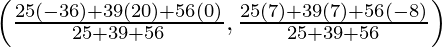
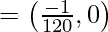
= (-1,0)
Hence, the coordinate of the centre of the circle is (-1,0)
Question 6. The base of an equilateral triangle with side 2a lies along the y-axis such that the mid-point of the base is at the origin. Find the vertices of the triangle.
Solution:
Since, ABC is an equilateral triangle it will have each sides equal, i.e, AB = BC = CA = 2a
Also, area of an equilateral triangle = 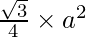 , where a is the side of the triangle.
, where a is the side of the triangle.
Therefore, area of given triangle = 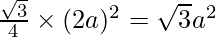
Also, area of a triangle = 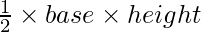
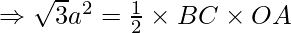
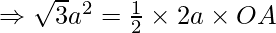
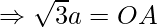
Thus, the coordinates of point A is 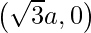
similarly, the coordinates of point B is (0,-a) and the coordinates of point C is (0,a)
Hence, the vertices of a triangle are (0,a), (0,-a) and 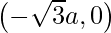 or (0,a), (0.-a) and
or (0,a), (0.-a) and 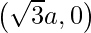
Question 7. Find the distance between P(x1,y1) and Q(x2,y2) when (i) PQ is parallel to the y-axis, (ii) PQ is parallel to the x-axis.
Solution:
We are given two points P(x1,y1) and Q(x2,y2),
(i) when line PQ is parallel to the y-axis, then we can conclude that the x-coordinate will be constant ⇒ x2 = x1
Thus, by using distance formula:
PQ = 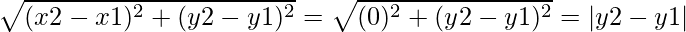
(ii) when line PQ is parallel to the x-axis, then we can conclude that the y-coordinate will be constant ⇒ y2 = y1
Thus, by using distance formula:
PQ = 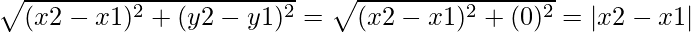
Question 8. Find a point on the x-axis, which is equidistant from the point (7,6) and (3,4).
Solution:
As given in the question, let the arbitrary point C that lies on the x-axis has coordinate (x,0). Now, this point is equidistant from both the coordinates (7,6) and (3,4), therefore by using distance formula, we get
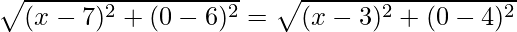
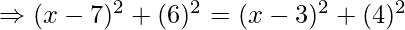
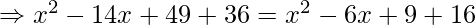
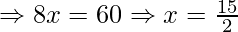
Therefore, coordinate of the point on the x-axis is 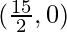
Share your thoughts in the comments
Please Login to comment...