Skip to content
Related Articles
Open in App
Not now

Related Articles

Class 11 RD Sharma Solutions – Chapter 29 Limits – Exercise 29.8 | Set 1

Improve Article
Save Article
  • Last Updated : 08 May, 2021
Improve Article
Save Article

Question 1. limx→π/2[π/2 – x].tanx

Solution:

We have,

limx→π/2[π/2 – x].tanx

Let us considered, y = [π/2 – x]

Here, x→π/2, y→0

= limy→0[y.tan(π/2 – y)]

= limy→0[y.{sin(π/2 – y)/cos(π/2 – y)]

= limy→0[y.{cosy/siny}]

= limy→0[y/siny].cosy

= limy→0[cosy]      [Since, limy→0[siny/y] = 1]

= 1

Question 2. limx→π/2[sin2x/cosx]

Solution:

We have,

limx→π/2[sin2x/cosx]

= limx→π/2[2sinx.cosx/cosx]

= 2Limx→π/2[sinx]

= 2

Question 3. limx→π/2[cos2x/(1 – sinx)]

Solution:

We have,

limx→π/2[cos2x/(1 – sinx)]

= limx→π/2[(1 – sin2x)/(1 – sinx)]

= limx→π/2[(1 – sinx)(1 + sinx)/(1 – sinx)]

= limx→π/2[(1 + sinx)]

= 1 + 1

= 2

Question 4. limx→π/2[(1 – sinx)/cos2x]

Solution:

We have,

limx→π/2[(1 – sinx)/cos2x]

= limx→π/2[(1 – sinx)/(1 – sin2x)]

= limx→π/2[(1 – sinx)/(1 – sinx)(1 + sinx)]

= limx→π/2[1/(1 + sinx)]

= 1/(1 + 1)

= 1/2

Question 5. limx→a[(cosx – cosa)/(x – a)]

Solution:

We have,

limx→a[(cosx – cosa)/(x – a)]

= \lim_{x\to a}[\frac{-2sin(\frac{x+a}{2})sin(\frac{x-a}{2})}{x-a}]

=-2\lim_{x\to a}[sin\frac{(x+a)}{2}]\lim_{x\to a}[\frac{sin\frac{(x-a)}{2}}{\frac{(x-a)}{2}×2}]

= -2sin[(a + a)/2] × 1 × (1/2)

= -sina

Question 6. limx→π/4[(1 – tanx)/(x – π/4)]

Solution:

We have,

limx→π/4[(1 – tanx)/(x – π/4)]

Let us considered, y = [x – π/4]

Here, x→π/4, y→0

= \lim_{y\to0}[\frac{1-tan(y+\frac{π}{4})}{y}]

= \lim_{y\to0}[\frac{1-\frac{(tany+tan\frac{π}{4})}{(1-tany.tan\frac{π}{4}}}{y}]

= \lim_{y\to0}[\frac{(1-tany-1-tany)}{y(1-tany)}]

= \lim_{y\to0}[\frac{-2tany}{y(1-tany)}]

= -2\lim_{y\to0}[\frac{tany}{y}]×\lim_{y\to0}[\frac{1}{(1-tany)}]

= -2 × 1 × [1/(1 – 0)]

= -2

Question 7. limx→π/2[(1 – sinx)/(π/4 – x)2]

Solution:

We have,

limx→π/2[(1 – sinx)/(π/4 – x)2]

Let us considered, y = [π/2 – x]

Here, x→π/2, y→0

= \lim_{y\to0}[\frac{1-sin(\frac{π}{2}-y)}{y^2}]

= limy→0[(1 – cosy)/y2]

= \lim_{y\to0}[\frac{2sin^2\frac{y}{2}}{(\frac{y}{2})^2×4}]

= 2 × 1 × (1/4)

= (1/2)

Question 8. limx→π/3[(√3 – tanx)/(π – 3x)]

Solution:

We have,

limx→π/3[(√3 – tanx)/(π – 3x)]

Let us considered, y = [π/3 – x]

When, x→π/3, y→0

= \lim_{y\to0}[\frac{\sqrt3-tan(\frac{π}{3}-y)}{3y}]

= \lim_{y\to0}[\frac{\sqrt3-\frac{(tan\frac{π}{3}-tany)}{(1+tany.tan\frac{π}{3}}}{3y}]

= \lim_{y\to0}[\frac{\sqrt3-\frac{(\sqrt{3}-tany)}{(1+\sqrt{3}.tany)}}{3y}]

= \lim_{y\to0}[\frac{4tany}{3y(1+\sqrt{3}tany)}]

= \frac{4}{3}\lim_{y\to0}[\frac{tany}{y}]×\lim_{y\to0}[\frac{1}{(1+\sqrt3tany)}]

= (4/3) × 1 × [1/(1 + 0)]

= (4/3)

Question 9. limx→a[(asinx – xsina)/(ax2 – xa2)]

Solution:

We have,

limx→a[(asinx – xsina)/(ax2 – xa2)]

= limx→a[(asinx – xsina)/{ax(x – a)}]

Let us considered, y = [x – a]

When, x→a, y→0

= limy→0[{asin(y + a) – (y + a)sina)}/{a(y + a)y}]

= limy→0[(a.siny.cosa + asina.cosy – ysina – asina)/{a(y + a)y}]

= limy→0[{a.siny.cosa + a.sina.(cosy – 1) – y.sina}/{a(y + a)y}]

= limy→0[{a.siny.cosa + a.sina.2sin2(y/2) – t.sina}/{a(y + a)y}]

= limy→0[a.siny.cosa/a(y + a)y] – limy→0[2.a.sina.sin2(y/2)/a(y + a)y] + limy→0[y.sina/a(a + y)y]

= [(a.cosa)/a2] – [(sina)/a2] + 0

= [(a.cosa – sina)/a2]

Question 10. limx→π/2[{√2 – √(1 + sinx)}/cos2x]

Solution:

We have,

limx→π/2[{√2 – √(1 + sinx)}/cos2x]

On rationalizing the numerator, we get

= limx→π/2[{2 – (1 + sinx)}/cos2x{√2 + √(1 + sinx)}]

= limx→π/2[(1 – sinx)/(1 – sin2x){√2 + √(1 + sinx)}]

= limx→π/2[(1 – sinx)/(1 – sinx)(1 + sinx){√2 + √(1 + sinx)}]

= limx→π/2[1/(1 + sinx){√2 + √(1 + sinx)}]

= 1/{(1 + 1)(√2 + √2)}

= 1/4√2

Question 11. limx→π/2[{√(2 – sinx) – 1}/(π/2 – x)2]

Solution:

We have,

limx→π/2[{√(2 – sinx) – 1}/(π/2 – x)2]

Let us considered, y = [π/2 – x]

Here, x→π/2, y→0

=\lim_{y\to0}[\frac{\sqrt{2-sin(\frac{π}{2}-y)}-1}{y^2}]

= limy→0[{√(2 – cosy) – 1}/y2]

On rationalizing the numerator, we get

= limy→0[{(2 – cosy) – 1}/y2{√(2 – cosy) – 1}]

= limy→0[{1 – cosy}/y2{√(2 – cosy) – 1}]

= \lim_{y\to0}[\frac{2sin^2\frac{y}{2}}{y^2(\sqrt{2-cosx}+1)}]

= \lim_{y\to0}[\frac{2sin^2\frac{y}{2}}{(\frac{y}{2})^2(\sqrt{2-cosx}+1)×4}]

= 2/4(1 + 1)

= 1/4

Question 12. limx→π/4[(√2 – cosx – sinx)/(π/4 – x)2]

Solution:

We have,

limx→π/4[(√2 – cosx – sinx)/(π/4 – x)2]

= \lim_{x\to \frac{π}{2}}\frac{\sqrt2[1-(\frac{1}{\sqrt2}.cosx+\frac{1}{\sqrt2}.sinx)]}{(\frac{π}{4}-x)^2}

= \lim_{x\to \frac{π}{2}}\frac{\sqrt{2}[1-cos(\frac{π}{4}-x)]}{(\frac{π}{4}-x)^2}

= \lim_{x\to \frac{π}{2}}\frac{[2\sqrt{2}sin^2\frac{(\frac{π}{4}-x)}{2}]}{(\frac{π}{4}-x)^2}

= 2\sqrt{2}\lim_{x\to \frac{π}{2}}\frac{[sin^2\frac{(\frac{π}{4}-x)}{2}]}{\frac{(\frac{π}{4}-x)}{4}^2×4}

= 2√2/4

= (1/√2)

Question 13. limx→π/8[(cot4x – cos4x)/(π – 8x)3]

Solution:

We have,

limx→π/8[(cot4x – cos4x)/(π – 8x)3]

= limx→π/8[(cot4x – cos4x)/83(π/8 – x)3]

Let us considered, (π/8 – x) = y

When x→π/8, y→0

=\lim_{x\to0}[\frac{cot(\frac{π}{2}-4x)-cos(\frac{π}{2}-4x)}{(π-8x)^3}]

= limx→0[(tan4x-sin4x)/83(π/8-x)3]

= limx→0[(sin4x/cos4x-sin4x)/83(π/8-x)3]

=\lim_{y\to0}[\frac{sin4y-sin4y.cos4y}{cos4y.8^3.y^3}]

=\lim_{y\to0}[\frac{sin4y(1-cos4y)}{cos4y.8^3.y^3}]

=\lim_{y\to0}[\frac{sin4y(2sin^22y)}{cos4y.8^3.y^3}]

=\frac{2}{8^3}\lim_{y\to0}\frac{sin4y}{y}×\lim_{y\to0}×\frac{sin^22y}{y^2}\lim_{y\to0}\frac{1}{cos4y}

=\frac{2}{8^3}\lim_{y\to0}\frac{sin4y}{4y}×4×\lim_{y\to0}×\frac{sin^22y}{(2y)^2}×4×\lim_{y\to0}\frac{1}{cos4y}

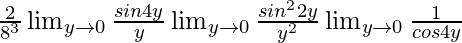
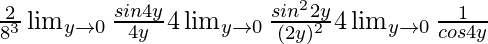
= (2 × 4 × 1 × 4 × 1)/(83)

= 1/16

Question 14. limx→a[(cosx – cosa)/(√x – √a)]

Solution:

We have,

limx→a[(cosx – cosa)/(√x – √a)]

= \lim_{x\to a}[\frac{-2sin(\frac{x+a}{2})sin(\frac{x-a}{2})}{\sqrt{x}-\sqrt{a}}]

On rationalizing the denominator, we get

= \lim_{x\to a}[\frac{-2sin(\frac{x+a}{2})sin(\frac{x-a}{2})(\sqrt{x}+\sqrt{a})}{x-a}]

= -2\lim_{x\to a}[sin\frac{(x+a)}{2}]\lim_{x\to a}[\frac{sin\frac{(x-a)}{2}}{\frac{(x-a)}{2}×2}]×\lim_{x\to a}(\sqrt{x}+\sqrt{a})

= -2 × sina × 1 × (1/2) × 2√a

= -2√a.sina

Question 15. limx→π[{√(5 + cosx) – 2}/(π – x)2]

Solution:

We have,

limx→π[{√(5 + cosx) – 2}/(π – x)2]

Let us considered, y = [π – x]

When, x→π, y→0

= \lim_{y\to0}[\frac{\sqrt{5+cos(π-y)}-2}{y^2}]

= limy→0[{√(5 – cosy) – 2}/y2]

On rationalizing the numerator, we get

= \lim_{y\to0}[\frac{5-cosy-4}{y^2(\sqrt{5-cosy}-2)}]

= limy→0[{1 – cosy}/y2{√(5 – cosy)-2}]

= \lim_{y\to0}[\frac{2sin^2\frac{y}{2}}{y^2(\sqrt{5-cosx}+2)}]

= \lim_{y\to0}[\frac{2sin^2\frac{y}{2}}{(\frac{y}{2})^2(\sqrt{5-cosx}+2)×4}]

= 2 × (1/4) × {1/(2 + 2)}

= (1/8)

Question 16. limx→a[(cos√x – cos√a)/(x – a)]

Solution:

We have,

limx→a[(cos√x – cos√a)/(x – a)]

= \lim_{x\to a}[\frac{-2sin(\frac{\sqrt{x}+\sqrt{a}}{2})sin(\frac{\sqrt{x}-\sqrt{a}}{2})}{(\sqrt{x}-\sqrt{a})(\sqrt{x}+\sqrt{a})}]

= -2\lim_{x\to a}[sin\frac{(\sqrt{x}+\sqrt{a})}{2}]\lim_{x\to a}[\frac{sin\frac{(\sqrt{x}-\sqrt{a})}{2}}{\frac{(\sqrt{x}-\sqrt{a})}{2}×2}]×\lim_{x\to a}\frac{1}{(\sqrt{x}+\sqrt{a})}

= -2sin√a × 1 × (1/2√a) × (1/2)

= -(sin√a/2√a)

Question 17. limx→a[(sin√x – sin√a)/(x – a)]

Solution:

We have,

limx→a[(sin√x – sin√a)/(x – a)]

= \lim_{x\to a}[\frac{2cos(\frac{\sqrt{x}+\sqrt{a}}{2})sin(\frac{\sqrt{x}-\sqrt{a}}{2})}{(\sqrt{x}-\sqrt{a})(\sqrt{x}+\sqrt{a})}]

= 2\lim_{x\to a}[cos\frac{(\sqrt{x}+\sqrt{a})}{2}]\lim_{x\to a}[\frac{sin\frac{(\sqrt{x}-\sqrt{a})}{2}}{\frac{(\sqrt{x}-\sqrt{a})}{2}×2}]×\lim_{x\to a}\frac{1}{(\sqrt{x}+\sqrt{a})}

= 2cos√a × 1 × (1/2√a) × (1/2)

= (cos√a/2√a)

Question 18. limx→1[(1 – x2)/sin2πx]

Solution:

We have,

limx→1[(1 – x2)/sin2πx]

When, x→1, h→0

= limh→0[{1-(1-h)2}/sin2π(1-h)]

= limh→0[(2h-h2)/-sin2πh]

= limh→0[{h(2-h)}/sin2πh]

=-\lim_{h\to0}[\frac{(2-h)}{\frac{sin2πh}{h}}]

= -\lim_{h\to0}[\frac{(2-h)}{(\frac{sin2πh}{2πh})×2π}]

= -2/2π

= -1/π

Question 19. limx→π/4[{f(x) – f(π/4)}/{x – π/4}]

Solution:

We have,

limx→π/4[{f(x) – f(π/4)}/{x – π/4}]

When, x→π/4, h→0

= limh→0[{f(π/4 + h) – f(π/4)}/{π/4 + h – π/4}]

It is given that f(x) = sin2x

= limh→0[{sin(π/2 + 2h) – sin(π/2)}/h]

= limh→0[(cos2h – 1)/h]

= limh→0[{-2sin2h}/h]

= -2Limh→0[(sinh/h)2] × h

= -2 × 1 × 0

= 0


My Personal Notes arrow_drop_up
Related Articles
1. Class 11 RD Sharma Solutions - Chapter 29 Limits - Exercise 29.10 | Set 2
2. Class 11 RD Sharma Solutions - Chapter 29 Limits - Exercise 29.5 | Set 1
3. Class 11 RD Sharma Solutions - Chapter 29 Limits - Exercise 29.5 | Set 2
4. Class 11 RD Sharma Solutions - Chapter 29 Limits - Exercise 29.10 | Set 3
5. Class 11 RD Sharma Solutions - Chapter 29 Limits - Exercise 29.4 | Set 1
6. Class 11 RD Sharma Solutions - Chapter 29 Limits - Exercise 29.4 | Set 2
7. Class 11 RD Sharma Solutions - Chapter 29 Limits - Exercise 29.6 | Set 1
8. Class 11 RD Sharma Solutions - Chapter 29 Limits - Exercise 29.6 | Set 2
9. Class 11 RD Sharma solutions - Chapter 29 Limits - Exercise 29.7 | Set 1
10. Class 11 RD Sharma solutions - Chapter 29 Limits - Exercise 29.7 | Set 2
Previous
Class 11 RD Sharma solutions - Chapter 29 Limits - Exercise 29.7 | Set 2
Next
Class 11 RD Sharma Solutions - Chapter 29 Limits - Exercise 29.8 | Set 2
Article Contributed By :
https://media.geeksforgeeks.org/auth/avatar.png
vivekray59
@vivekray59
Vote for difficulty
Article Tags :
Report Issue
We use cookies to ensure you have the best browsing experience on our website. By using our site, you acknowledge that you have read and understood our Cookie Policy & Privacy Policy
Lightbox

Start Your Coding Journey Now!