Question 16: In △ABC, prove the following:
a2 (cos2 B – cos2 C) + b(cos2 C – cos2 A) + c(cos2 A – cos2 B) = 0
Solution:
According to the sine rule

Considering LHS, we have
= a2 (cos2 B – cos2 C) + b(cos2 C – cos2 A) + c(cos2 A – cos2 B)
By using trigonometric formula,
cos2 a = 1 – sin2 a
= λ2 sin2 A(1-sin2 B – (1-sin2 C)) + λ2 sin2 B(1-sin2 C – (1-sin2 A)) + λ2 sin2 C(1-sin2 A – (1-sin2 B))
= λ2 sin2 A(1-sin2 B – 1+ sin2 C) + λ2 sin2 B(1-sin2 C – 1 + sin2 A) + λ2 sin2 C(1-sin2 A – 1+sin2 B)
= λ2 sin2 A(sin2 C – sin2 B) + λ2 sin2 B(sin2 A – sin2 C) + λ2 sin2 C(sin2 B – sin2 A)
= λ2 (sin2 A sin2 C – sin2 A sin2 B + sin2 B sin2 A – sin2 B sin2 C + sin2 C sin2 B – sin2 C sin2 A)
= λ2 (0)
=0
As LHS = RHS
Hence, proved!!
Question 17: In △ABC, prove the following:
b cos B + c cos C = a cos (B-C)
Solution:
According to the sine rule

Considering LHS, we have
= b cos B + c cos C
= λ sin B cos B + λ sin C cos C
= λ (sin B cos B + sin C cos C)
=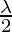 (2 sin B cos B + 2 sin C cos C)
(2 sin B cos B + 2 sin C cos C)
By using trigonometric formula,
2 sin a cos a = sin 2a
=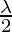 (sin 2B + sin 2C) ………………………..(1)
(sin 2B + sin 2C) ………………………..(1)
Now considering RHS, we have
= a cos (B-C)
= λ sin A cos (B-C)
=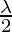 (2 sin A cos (B-C))
(2 sin A cos (B-C))
By using trigonometric formula,
2 sin a cos b = sin (a+b) + sin(a-b)
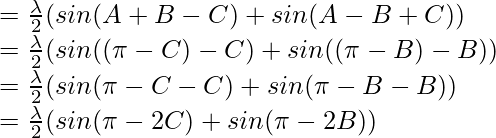
=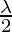 (sin 2C + sin2B) ……………………….(2)
(sin 2C + sin2B) ……………………….(2)
As LHS = RHS
Hence, proved!!
Question 18: In △ABC, prove the following:
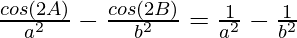
Solution:
According to the sine rule

Considering LHS, we have
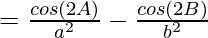
By using trigonometric formula,
cos 2a = 1-2sin2a
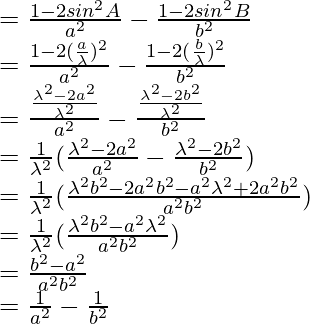
As LHS = RHS
Hence, proved!!
Question 19: In △ABC, prove the following:
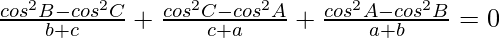
Solution:
According to the sine rule

Considering LHS, we have
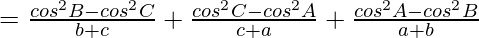
Now taking,
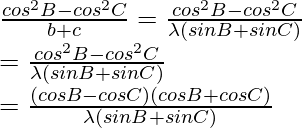
By using trigonometric formula,
cos a + cos b = 2 cos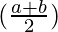 cos
cos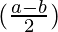
cos a – cos b = -2 sin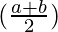 sin
sin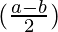
sin a + sin b = 2 sin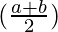 cos
cos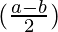
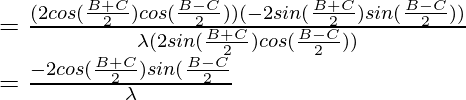
By using trigonometric formula,
2 cos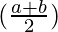 sin
sin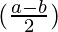 = sin a – sin b
= sin a – sin b
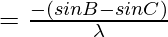
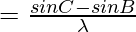 ………………(1)
………………(1)
Similarly, we can prove,
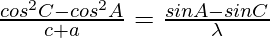 ……………….(2)
……………….(2)
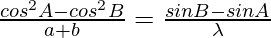 ………………..(3)
………………..(3)
Adding (1), (2) and (3), we get
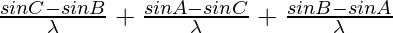
= 0
As LHS = RHS
Hence, proved!!
Question 20: In △ABC, prove the following:
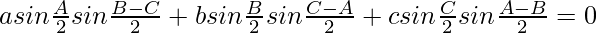
Solution:
According to the sine rule

Considering LHS, we have
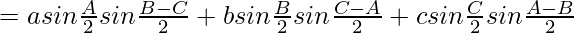
Now taking,
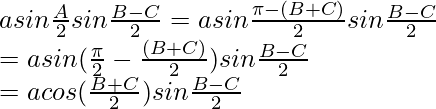
=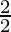 a cos
a cos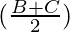 sin
sin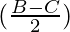
=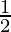 (sin B – sin C)
(sin B – sin C)
=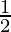 (a sin B – a sin C)
(a sin B – a sin C)
=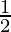 (a sin B – a sin C)
(a sin B – a sin C)
=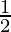 (b sin A – a sin C) ………………..(1)
(b sin A – a sin C) ………………..(1)
Similarly, we can prove,
b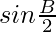 sin
sin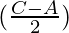 =
=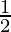 (b sin C – b sin A) ……………….(2)
(b sin C – b sin A) ……………….(2)
c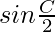 sin
sin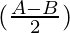 =
=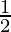 (a sin C – b sin C) ………………..(3)
(a sin C – b sin C) ………………..(3)
Adding (1), (2) and (3), we get
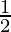 (b sin A – a sin C) +
(b sin A – a sin C) +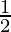 (b sin C – b sin A) +
(b sin C – b sin A) +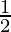 (a sin C – b sin C)
(a sin C – b sin C)
=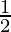 (b sin A – a sin C + b sin C – b sin A + a sin C – b sin C)
(b sin A – a sin C + b sin C – b sin A + a sin C – b sin C)
= 0
As LHS = RHS
Hence, proved!!
Question 21: In △ABC, prove the following:
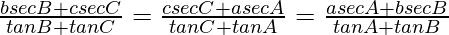
Solution:
According to the sine rule

Considering equation, we have
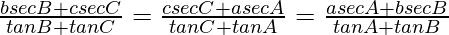
Now taking,
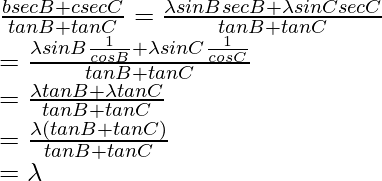
Similarly, we can prove,
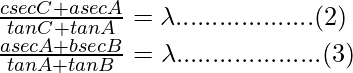
From, (1), (2) and (3), we get
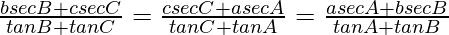
Hence, proved!!
Question 22: In △ABC, prove the following:
a cos A + b cos B + c cos C = 2b sin A sin C = 2c sin A sin B
Solution:
According to the sine rule

Considering LHS equation, we have
a cos A + b cos B + c cos C = λ sin A cos A + λ sin B cos B + λ sin C cos C
= λ (sin A cos A + sin B cos B + sin C cos C)
=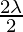 (sin A cos A + sin B cos B + sin C cos C)
(sin A cos A + sin B cos B + sin C cos C)
=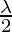 (2 sin A cos A + 2 sin B cos B + 2 sin C cos C)
(2 sin A cos A + 2 sin B cos B + 2 sin C cos C)
By using trigonometric formula,
2 sin a cos a = sin 2a
=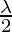 (sin 2A + sin 2B + 2 sin C cos C)
(sin 2A + sin 2B + 2 sin C cos C)
By using trigonometric formula,
sin a + sin b = 2 sin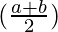 cos
cos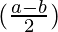
=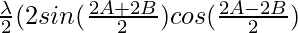 + 2 sin C cos C)
+ 2 sin C cos C)
=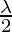 (2 sin (A+B) cos(A-B) + 2 sin C cos C)
(2 sin (A+B) cos(A-B) + 2 sin C cos C)
=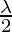 (2 sin (π-C) cos(A-B) + 2 sin C cos C)
(2 sin (π-C) cos(A-B) + 2 sin C cos C)
=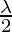 (2 sin C cos(A-B) + 2 sin C cos C)
(2 sin C cos(A-B) + 2 sin C cos C)
=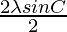 (cos(A-B) + cos C)
(cos(A-B) + cos C)
= λ sin C (cos(A-B) + cos (π-(A+B)))
= λ sin C (cos(A-B) + (-cos (A+B)))
= λ sin C (cos(A-B) – cos (A+B))
= λ sin C (2 sin A sin B)
= 2 λ sin A sin B sin C
Now putting λ sin C = c and λ sin B = b, we get
2 c sin A sin B and 2 b sin A sin C
Hence, proved!!
Question 23: In △ABC, prove the following:
a (cos B cos C + cos A) = b (cos C cos A + cos B) = c (cos C cos A + cos C)
Solution:
According to the sine rule

Considering equation, we have
a (cos B cos C + cos A) = λ sin A (cos B cos C + cos A)
= λ (sin A cos B cos C + sin A cos A)
= λ (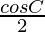 (2 sin A cos B) + sin A cos A)
(2 sin A cos B) + sin A cos A)
= λ (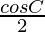 (sin (A+B) + sin (A-B)) + sin A cos A)
(sin (A+B) + sin (A-B)) + sin A cos A)
= λ (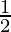 (cos C sin (A+B) + cos C sin (A-B)) + sin A cos A)
(cos C sin (A+B) + cos C sin (A-B)) + sin A cos A)
= λ (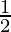 (\frac{1}{2} (2 cos C sin (A+B) + 2 cos C sin (A-B))) + sin A cos A)
(\frac{1}{2} (2 cos C sin (A+B) + 2 cos C sin (A-B))) + sin A cos A)
= λ (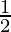 (2 cos C sin (A+B) + 2 cos C sin (A-B)) + sin A cos A)
(2 cos C sin (A+B) + 2 cos C sin (A-B)) + sin A cos A)
By using trigonometric formula,
2 sin a cos b = sin (a+b) + sin (a-b)
= λ (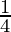 (sin (A+B+C) + sin (A+B-C) + sin (A-B+C) + sin (A-B-C)) + sin A cos A)
(sin (A+B+C) + sin (A+B-C) + sin (A-B+C) + sin (A-B-C)) + sin A cos A)
= λ (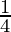 (sin (π) + sin ((π-C)-C) + sin ((π-B)-B) + sin (A-(B+C)) +
(sin (π) + sin ((π-C)-C) + sin ((π-B)-B) + sin (A-(B+C)) +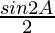 )
)
= λ (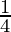 (0 + sin (π-2C) + sin (π-2B) + sin (2A-π) +
(0 + sin (π-2C) + sin (π-2B) + sin (2A-π) +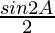 )
)
= λ (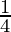 (sin 2C + sin 2B – sin 2A +
(sin 2C + sin 2B – sin 2A +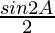 )
)
=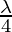 (sin 2C + sin 2B + sin 2A)
(sin 2C + sin 2B + sin 2A)
Similarly,
b (cos C cos A + cos B) =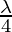 (sin 2C + sin 2B + sin 2A)
(sin 2C + sin 2B + sin 2A)
c (cos C cos A + cos C) =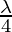 (sin 2C + sin 2B + sin 2A)
(sin 2C + sin 2B + sin 2A)
Hence, proved!!
Question 24: In △ABC, prove the following:
a (cos C – cos B) = 2 (b-c)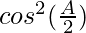
Solution:
According to the sine rule

Considering equation, we have
a (cos C – cos B) = λ sin A (cos C – cos B)
= λ (sin A cos C – sin A cos B)
=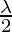 (2 sin A cos C – 2 sin A cos B)
(2 sin A cos C – 2 sin A cos B)
By using trigonometric formula,
2 sin a cos b = sin (a+b) + sin (a-b)
=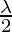 (sin (A+C) + sin (A-C) – (sin (A+B) + sin (A-B)))
(sin (A+C) + sin (A-C) – (sin (A+B) + sin (A-B)))
=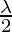 (sin (A+C) + sin (A-C) – sin (A+B) – sin (A-B))
(sin (A+C) + sin (A-C) – sin (A+B) – sin (A-B))
=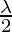 (sin (π-B) + sin (A-C) – sin (π-C) – sin (A-B))
(sin (π-B) + sin (A-C) – sin (π-C) – sin (A-B))
=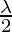 (sin B – sin C + sin (A-C) – sin (A-B))
(sin B – sin C + sin (A-C) – sin (A-B))
By using trigonometric formula,
sin a – sin b = 2 sin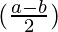 cos
cos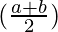
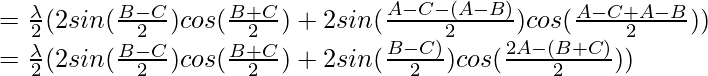
= λ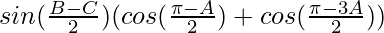
= λ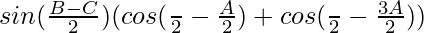
= λ sin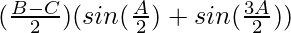
By using trigonometric formula,
sin a + sin b = 2 sin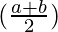 cos
cos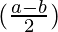
= λ sin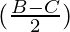
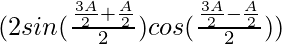
= λ sin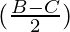
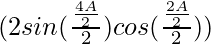
= λ sin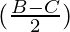 (2 sin A cos
(2 sin A cos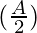 )
)
= 2 λ sin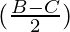 (2 sin
(2 sin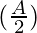 cos
cos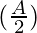 ) cos
) cos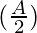
= 4 λ sin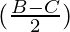 sin
sin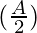 [Tex]cos^2(\frac{A}{2})[/Tex]
[Tex]cos^2(\frac{A}{2})[/Tex]
= 4 λ sin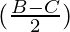 cos
cos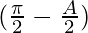 [Tex]cos^2(\frac{A}{2})[/Tex]
[Tex]cos^2(\frac{A}{2})[/Tex]
= 4 λ sin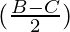 cos
cos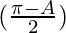 [Tex]cos^2(\frac{A}{2})[/Tex]
[Tex]cos^2(\frac{A}{2})[/Tex]
= 4 λ sin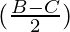 cos
cos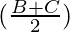 [Tex]cos^2(\frac{A}{2})[/Tex]
[Tex]cos^2(\frac{A}{2})[/Tex]
= 2 λ (2 sin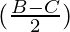 cos
cos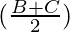 )
)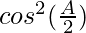
By using trigonometric formula,
2 cos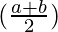 sin
sin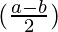 = sin a – sin b
= sin a – sin b
= 2 λ (sin B – sin A)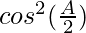
= 2 (λ sin B – λ sin A)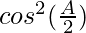
= 2 (b – a)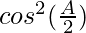
As LHS = RHS
Hence, proved!!
Question 25: In △ABC, prove the following:
b cos θ = c cos(A-θ)+a cos(C+θ)
Solution:
According to the sine rule

Considering RHS, equation, we have
c cos(A-θ)+a cos(C+θ) = λ sin C cos(A-θ) + λ sin A cos(C+θ)
= λ (sin C cos(A-θ) + sin A cos(C+θ))
=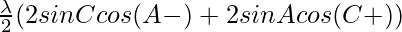
By using trigonometric formula,
2 sin a cos b = sin (a+b) + sin (a-b)
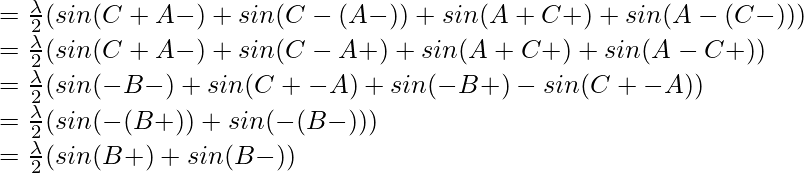
By using trigonometric formula,
sin (a+b) + sin (a-b) = 2 sin a cos b
=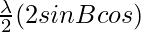
= λ sin B cos θ
= b cos θ
As LHS = RHS
Hence, proved!!
Question 26: In △ABC, if sin2A + sin2B = sin2C. Show that the triangle is right-angled.
Solution:
According to the sine rule

Considering equation, we have
sin2 A + sin2 B = sin2 C
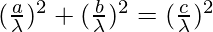
a2 + b2 = c2
Hence, proved, the triangle is right-angled as c as hypotenuse.
Question 27: In △ABC, if a2, b2, and c2 are in AP. Prove that cot A, cot B, and cot C are also in AP.
Solution:
We have a2, b2 and c2 in AP
2a2, 2b2 and 2c2 are also in AP
(a2+b2+c2)-2a2, (a2+b2+c2)-2b2 and (a2+b2+c2)-2c2 are also in AP
b2+c2-a2, a2+c2-b2 and a2+b2-c2 are also in AP
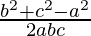 ,
,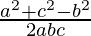 and
and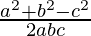 are also in AP
are also in AP
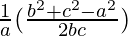 ,
,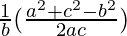 and
and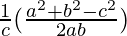 are also in AP
are also in AP
According to the cosine rule
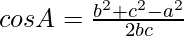
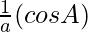 ,
,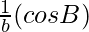 and
and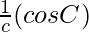 are also in AP
are also in AP
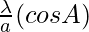 ,
,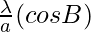 and
and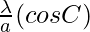 are also in AP
are also in AP
According to the sine rule

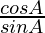 ,
,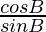 and
and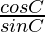 are also in AP
are also in AP
cot A, cot B and cot C are also in AP
Hence, proved !!
Question 28: The upper part of a tree broken by the wind makes an angle of 30° with the ground and the distance from the root to the point where the top of the tree touches the ground is 15 m. Using sine rule, find the height of the tree.
Solution:
Suppose BD be the tree and the upper part of the tree is broken over by the wind at point A.

The total height of the tree is x+y.
In △ABC, ∠C = 30° and ∠B = 90°
∠A = 60° (Triangle angle sum property)
According to the sine rule
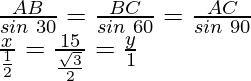
2x =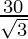 = y
= y
Hence, x =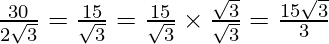 = 5√3
= 5√3
and y =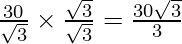 = 10√3
= 10√3
So, the height of tree x+y = 5√3+10√3
= 15√3 m
Question 29: At the foot of a mountain, the elevation of it summit is 45°, after ascending 1000m towards the mountain up a slope of 30° inclination, the elevation is found to be 60°. Find the height of the mountain.
Solution:
Suppose, AB is a mountain of height t+x.
c = 1000m

In △DFC,
sin 30° =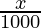
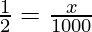
x =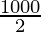 = 500 m
= 500 m
And, tan 30° =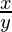
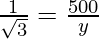
y = 500√3 m
Now, In △ABC
tan 45° =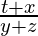
1 =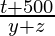
500√3+z = t+500
500(√3-1)+z = t …………………..(1)
Now, In △ADE
tan 60° =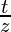
√3 =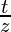
t = √3z ………………….(2)
From (1) and (2), we get
z = 500 m
t = 500√3 m
So, the height of the mountain = t+x = 500√3 + 500 = 500(√3+1)m
Question 30: A person observes the angle of elevation of the peak of a hill from a station to be α. He walks c metres along a slope inclined at an angle β and finds the angle of elevation of the peak of the hill to be γ. Show that the height of the peak above the ground is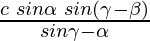
Solution:
Suppose, AB is a peak whose height above the ground is t+x,

In △DFC,
sin β =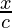
x = c sin β ………………………..(1)
And, tan β =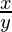
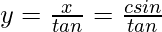 = c cos β ………………………..(2)
= c cos β ………………………..(2)
Now, In △ADE
tan γ =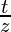
z = t cot γ ………………………(3)
Now, In △ABC
tan α=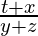
t +x = tan α (y+z)
From (1), (2) and (3), we get
t + c sin β = tan α (c cos β+t cot γ)
t + c sin β = c tan α cos β + t tan α cot γ
t – t tan α cot γ = c tan α cos β – c sin β
t(1 – tan α cot γ) = c (tan α cos β – sin β)
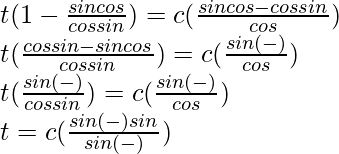
Now,

Hence proved !!
Question 31: If the sides a, b and c of △ABC are in H.P. Prove that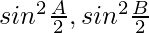 and
and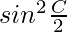 are in H.P
are in H.P
Solution:
If the sides a, b and c of △ABC are in H.P
Then,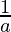 ,
,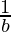 and
and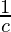 are in AP
are in AP
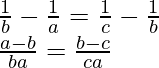
According to the sine rule

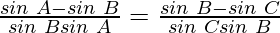
By using trigonometric formula,
sin a – sin b = 2 sin cos
cos
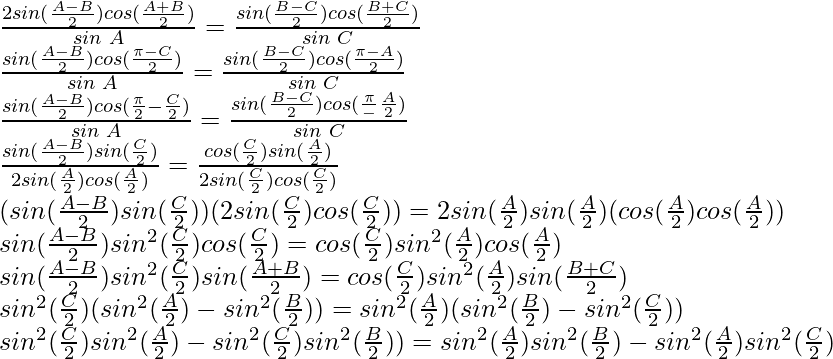
Divide by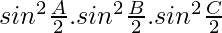 , we get
, we get
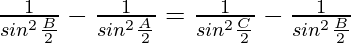
Hence,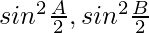 and
and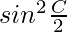 are in H.P
are in H.P
Share your thoughts in the comments
Please Login to comment...