Question 1. Express each of the following as the product of sines and cosines:
(i) sin 12θ + sin 4θ
Solution:
We know, sin A + sin B = 2 sin (A+B)/2 cos (A–B)/2
sin 12θ + sin 4θ = 2 sin (12θ + 4θ)/2 cos (12θ – 4θ)/2
= 2 sin 16θ/2 cos 8θ/2
= 2 sin 8θ cos 4θ
(ii) sin 5θ – sin θ
Solution:
We know, sin A – sin B = 2 cos (A+B)/2 sin (A–B)/2
sin 5θ – sin θ = 2 cos (5θ + θ)/2 sin (5θ – θ)/2
= 2 cos 6θ/2 sin 4θ/2
= 2 cos 3θ sin 2θ
(iii) cos 12θ + cos 8θ
Solution:
We know, cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2
cos 12θ + cos 8θ = 2 cos (12θ + 8θ)/2 cos (12θ – 8θ)/2
= 2 cos 20θ/2 cos 4θ/2
= 2 cos 10θ cos 2θ
(iv) cos 12θ – cos 4θ
Solution:
We know, cos A – cos B = –2 sin (A+B)/2 sin (A–B)/2
cos 12θ – cos 4θ = –2 sin (12θ + 4θ)/2 sin (12θ – 4θ)/2
= –2 sin 16θ/2 sin 8θ/2
= –2 sin 8θ sin 4θ
(v) sin 2θ + cos 4θ
Solution:
sin 2θ + cos 4θ = sin 2θ + sin (90o – 4θ)
We know, sin A + sin B = 2 sin (A+B)/2 cos (A–B)/2
sin 2θ + sin (90o – 4θ) = 2 sin (2x + 90o – 4θ)/2 cos (2θ – 90o + 4θ)/2
= 2 sin (90o – 2θ)/2 cos (6θ – 90o)/2
= 2 sin (45o – θ) cos (3θ – 45o)
= 2 sin (45o – θ) cos [–(45o – 3θ)]
= 2 sin (45o – θ) cos (45o – 3θ)
= 2 sin (π/4 – θ) cos (π/4 – 3θ)
Question 2. Prove that :
(i) sin 38° + sin 22° = sin 82°
Solution:
Given, L.H.S. = sin 38° + sin 22°.
We know, sin A + sin B = 2 sin (A+B)/2 cos (A–B)/2
sin 38° + sin 22° = 2 sin (38o + 22o)/2 cos (38o – 22o)/2
= 2 sin 60o/2 cos 16o/2
= 2 sin 30o cos 8o
= 2 × (1/2) × cos 8o
= cos 8o
= cos (90° – 82°)
= sin 82°
= R.H.S.
Hence proved.
(ii) cos 100° + cos 20° = cos 40°
Solution:
Given, L.H.S. = cos 100° + cos 20°.
We know, cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2
cos 100° + cos 20° = 2 cos (100o + 20o)/2 cos (100o – 20o)/2
= 2 cos 120o/2 cos 80o/2
= 2 cos 60o cos 40o
= 2 × (1/2) × cos 40o
= cos 40o
= R.H.S.
Hence Proved.
(iii) sin 50° + sin 10° = cos 20°
Solution:
Given, L.H.S. = sin 50° + sin 10°.
We know, sin A + sin B = 2 sin (A+B)/2 cos (A–B)/2.
sin 50° + sin 10° = 2 sin (50o + 10o)/2 cos (50o – 10o)/2
= 2 sin 60o/2 cos 40o/2
= 2 sin 30o cos 20o
= 2 × (1/2) × cos 20o
= cos 20o
= R.H.S
Hence Proved.
(iv) sin 23° + sin 37° = cos 7°
Solution:
Given L.H.S. = sin 23° + sin 37°.
We know sin A + sin B = 2 sin (A+B)/2 cos (A–B)/2
sin 23° + sin 37° = 2 sin (23o + 37o)/2 cos (23o – 37o)/2
= 2 sin 60o/2 cos (–14o/2)
= 2 sin 30o cos (–7o)
= 2 × (1/2) × cos 7o
= cos 7o
= R.H.S.
Hence Proved.
(v) sin 105° + cos 105° = cos 45°
Solution:
Given, L.H.S. = sin 105° + cos 105°
sin 105° + cos 105° = sin 105o + sin (90o – 105o)
= sin 105o + sin (–15o)
= sin 105o – sin 15o
We know, sin A – sin B = 2 cos (A+B)/2 sin (A–B)/2
sin 105o – sin 15o = 2 cos (105o + 15o)/2 sin (105o – 15o)/2
= 2 cos 120o/2 sin 90o/2
= 2 cos 60o sin 45o
= 2 × (1/2) × (1/√2)
= 1/√2
= cos 45o
= R.H.S.
Hence Proved.
(vi) sin 40° + sin 20° = cos 10°
Solution:
Given, L.H.S. = sin 40° + sin 20°.
We know, sin A + sin B = 2 sin (A+B)/2 cos (A–B)/2
sin 40° + sin 20° = 2 sin (40o + 20o)/2 cos (40o – 20o)/2
= 2 sin 60o/2 cos 20o/2
= 2 sin 30o cos 10o
= 2 × (1/2) × cos 10o
= cos 10o
= R.H.S.
Hence Proved.
Question 3. Prove that:
(i) cos 55° + cos 65° + cos 175° = 0
Solution:
Given, L.H.S. = cos 55° + cos 65° + cos 175°.
We know, cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2
cos 55° + cos 65° + cos 175° = 2 cos (55o + 65o)/2 cos (55o – 65o) + cos (180o – 5o)
= 2 cos 120o/2 cos (–10o)/2 – cos 5o
= 2 cos 60° cos (–5°) – cos 5°
= 2 × (1/2) × cos 5o – cos 5o
= cos 5o – cos 5o
= 0
= R.H.S.
Hence Proved.
(ii) sin 50° – sin 70° + sin 10° = 0
Solution:
Given, L.H.S. = sin 50° – sin 70° + sin 10°.
We know, sin A – sin B = 2 cos (A+B)/2 sin (A–B)/2
sin 50° – sin 70° + sin 10° = 2 cos (50o + 70o)/2 sin (50o – 70o) + sin 10o
= 2 cos 120o/2 sin (–20o)/2 + sin 10o
= 2 cos 60o (–sin 10o) + sin 10o
= 2 × (1/2) × (–sin 10o) + sin 10o
= 0
= R.H.S.
Hence Proved.
(iii) cos 80° + cos 40° – cos 20° = 0
Solution:
Given L.H.S. = cos 80° + cos 40° – cos 20°.
We know, cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2
cos 80° + cos 40° – cos 20° = 2 cos (80o + 40o)/2 cos (80o – 40o) – cos 20o
= 2 cos 120o/2 cos 40o/2 – cos 20o
= 2 cos 60° cos 20o – cos 20°
= 2 × (1/2) × cos 20o – cos 20o
= 0
= R.H.S.
Hence Proved.
(iv) cos 20° + cos 100° + cos 140° = 0
Solution:
Given, L.H.S. = cos 20° + cos 100° + cos 140°.
We know, cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2.
cos 20° + cos 100° + cos 140° = 2 cos (20o + 100o)/2 cos (20o – 100o) + cos (80o – 40o)
= 2 cos 120o/2 cos (–80o)/2 – cos 40o
= 2 cos 60° cos (–40°) – cos 40°
= 2 × (1/2) × cos 40o – cos 40o
= 0
= R.H.S.
Hence Proved.
(v) sin 5π/18 – cos 4π/9 = √3 sin π/9
Solution:
Given, L.H.S. = sin 5π/18 – cos 4π/9
= sin 5π/18 – sin (π/2 – 4π/9)
= sin 5π/18 – sin (9π – 8π)/18
= sin 5π/18 – sin π/18
We know, sin A – sin B = 2 cos (A+B)/2 sin (A– B)/2
= 2 cos (6π/36) sin (4π/36)
= 2 cos π/6 sin π/9
= 2 cos 30o sin π/9
= 2 × (√3/2) × sin π/9
= √3 sin π/9
= R.H.S.
Hence Proved.
(vi) cos π/12 – sin π/12 = 1/√2
Solution:
Given, cos π/12 – sin π/12 = sin (π/2 – π/12) – sin π/12
= sin (6π – 5π)/12 – sin π/12
= sin 5π/12 – sin π/12
We know, sin A – sin B = 2 cos (A+B)/2 sin (A–B)/2
= 2 cos (6π/24) sin (4π/24)
= 2 cos π/4 sin π/6
= 2 cos 45o sin 30o
= 2 × (1/√2) × (1/2)
= 1/√2
= R.H.S.
Hence Proved.
(vii) sin 80° – cos 70° = cos 50°
Solution:
We have, sin 80° = cos 50° + cos 70o
Here, R.H.S. = cos 50° + cos 70o
We know,
cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2
cos 50° + cos 70o = 2 cos (50o + 70o)/2 cos (50o – 70o)/2
= 2 cos 120o/2 cos (–20o)/2
= 2 cos 60o cos (–10o)
= 2 × (1/2) × cos 10o
= cos 10o
= cos (90° – 80°)
= sin 80°
= L.H.S.
Hence Proved.
(viii) sin 51° + cos 81° = cos 21°
Solution:
Given, L.H.S. = sin 51° + cos 81°
= sin 51o + sin (90o – 81o)
= sin 51o + sin 9o
We know, sin A + sin B = 2 sin (A+B)/2 cos (A–B)/2
sin 51o + sin 9o = 2 sin (51o + 9o)/2 cos (51o – 9o)/2
= 2 sin 60o/2 cos 42o/2
= 2 sin 30o cos 21o
= 2 × (1/2) × cos 21o
= cos 21o
= R.H.S.
Hence Proved.
Question 4. Prove that:
(i) cos (3π/4 + x) – cos (3π/4 – x) = –√2 sin x
Solution:
Given, L.H.S. = cos (3π/4 + x) – cos (3π/4 – x)
We know, cos A – cos B = –2 sin (A+B)/2 sin (A–B)/2
cos (3π/4 + x) – cos (3π/4 – x) = –2 sin (3π/4 + x + 3π/4 – x)/2 sin (3π/4 + x – 3π/4 + x)/2
= –2 sin (6π/4)/2 sin 2x/2
= –2 sin 6π/8 sin x
= –2 sin 3π/4 sin x
= –2 sin (π – π/4) sin x
= –2 sin π/4 sin x
= –2 × (1/√2) × sin x
= –√2 sin x
= R.H.S.
Hence proved.
(ii) cos (π/4 + x) + cos (π/4 – x) = √2 cos x
Solution:
Given, L.H.S. = cos (π/4 + x) + cos (π/4 – x)
We know, cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2
cos (π/4 + x) + cos (π/4 – x) = 2 cos (π/4 + x + π/4 – x)/2 cos (π/4 + x – π/4 + x)/2
= 2 cos (2π/4)/2 cos 2x/2
= 2 cos 2π/8 cos x
= 2 sin π/4 cos x
= 2 × (1/√2) × cos x
= √2 cos x
= R.H.S.
Hence proved.
Question 5. Prove that:
(i) sin 65o + cos 65o = √2 cos 20o
Solution:
Given L.H.S. = sin 65o + cos 65o
= sin 65o + sin (90o – 65o)
= sin 65o + sin 25o
We know, sin A + sin B = 2 sin (A+B)/2 cos (A–B)/2
sin 65o + sin 25o = 2 sin (65o + 25o)/2 cos (65o – 25o)/2
= 2 sin 90o/2 cos 40o/2
= 2 sin 45o cos 20o
= 2 × (1/√2) × cos 20o
= √2 cos 20o
= R.H.S.
Hence proved.
(ii) sin 47o + cos 77o = cos 17o
Solution:
Given, L.H.S. = sin 47o + cos 77o
= sin 47o + sin (90o – 77o)
= sin 47o + sin 13o
We know, sin A + sin B = 2 sin (A+B)/2 cos (A–B)/2
sin 47o + sin 13o = 2 sin (47o + 13o)/2 cos (47o – 13o)/2
= 2 sin 60o/2 cos 34o/2
= 2 sin 30o cos 17o
= 2 × (1/2) × cos 17o
= cos 17o
= R.H.S.
Hence proved.
Question 6. Prove that:
(i) cos 3A + cos 5A + cos 7A + cos 15A = 4 cos 4A cos 5A cos 6A
Solution:
Given, L.H.S. = cos 3A + cos 5A + cos 7A + cos 15A
= (cos 5A + cos 3A) + (cos 15A + cos 7A)
We know, cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2
= (cos 5A + cos 3A) + (cos 15A + cos 7A)
= [2 cos (5A+3A)/2 cos (5A–3A)/2] + [2 cos (15A+7A)/2 cos (15A–7A)/2]
= [2 cos 8A/2 cos 2A/2] + [2 cos 22A/2 cos 8A/2]
= [2 cos 4A cos A] + [2 cos 11A cos 4A]
= 2 cos 4A (cos 11A + cos A)
= 2 cos 4A [2 cos (11A+A)/2 cos (11A-A)/2]
= 2 cos 4A [2 cos 12A/2 cos 10A/2]
= 2 cos 4A [2 cos 6A cos 5A]
= 4 cos 4A cos 5A cos 6A
= R.H.S.
Hence proved.
(ii) cos A + cos 3A + cos 5A + cos 7A = 4 cos A cos 2A cos 4A
Solution:
Given L.H.S. = cos A + cos 3A + cos 5A + cos 7A
= (cos 3A + cos A) + (cos 7A + cos 5A)
We know, cos A + cos B = 2 cos (A+B)/2 cos (A–B)/2
= (cos 3A + cos A) + (cos 7A + cos 5A)
= [2 cos (3A+A)/2 cos (3A–A)/2] + [2 cos (7A+5A)/2 cos (7A–5A)/2]
= [2 cos 4A/2 cos 2A/2] + [2 cos 12A/2 cos 2A/2]
= [2 cos 2A cos A] + [2 cos 6A cos A]
= 2 cos A (cos 6A + cos 2A)
= 2 cos A [2 cos (6A+2A)/2 cos (6A–2A)/2]
= 2 cos A [2 cos 8A/2 cos 4A/2]
= 2 cos A [2 cos 4A cos 2A]
= 4 cos A cos 2A cos 4A
= R.H.S.
Hence proved.
(iii) sin A + sin 2A + sin 4A + sin 5A = 4 cos A/2 cos 3A/2 sin 3A
Solution:
Given, L.H.S. = sin A + sin 2A + sin 4A + sin 5A
= (sin 2A + sin A) + (sin 5A + sin 4A)
We know, sin A + sin B = 2 sin (A+B)/2 cos (A–B)/2
= (sin 2A + sin A) + (sin 5A + sin 4A)
= [2 sin (2A+A)/2 cos (2A–A)/2] + [2 sin (5A+4A)/2 cos (5A–4A)/2]
= [2 sin 3A/2 cos A/2] + [2 sin 9A/2 cos A/2]
= 2 cos A/2 (sin 9A/2 + sin 3A/2)
= 2 cos A/2 [2 sin (9A/2 + 3A/2)/2 cos (9A/2 – 3A/2)/2]
= 2 cos A/2 [2 sin ((9A+3A)/2)/2 cos ((9A–3A)/2)/2]
= 2 cos A/2 [2 sin 12A/4 cos 6A/4]
= 2 cos A/2 [2 sin 3A cos 3A/2]
= 4 cos A/2 cos 3A/2 sin 3A
= R.H.S.
Hence proved.
(iv) sin 3A + sin 2A – sin A = 4 sin A cos A/2 cos 3A/2
Solution:
Given, L.H.S. = sin 3A + sin 2A – sin A
= (sin 3A – sin A) + sin 2A
We know, sin A – sin B = 2 cos (A+B)/2 sin (A–B)/2
= (sin 3A – sin A) + sin 2A
= 2 cos (3A + A)/2 sin (3A – A)/2 + sin 2A
= 2 cos 4A/2 sin 2A/2 + sin 2A
= 2 cos 2A sin A + 2 sin A cos A
= 2 sin A (cos 2A + cos A)
= 2 sin A [2 cos (2A+A)/2 cos (2A-A)/2]
= 2 sin A [2 cos 3A/2 cos A/2]
= 4 sin A cos A/2 cos 3A/2
= R.H.S.
Hence proved.
(v) cos 20o cos 100o + cos 100o cos 140o – cos 140o cos 200o = – 3/4
Solution:
Given L.H.S. = cos 20o cos 100o + cos 100o cos 140o – cos 140o cos 200o
= 1/2 [2 cos 100o cos 20o + 2 cos 140o cos 100o – 2 cos 200o cos 140o]
We know that, 2 cos A cos B = cos (A+B) + cos (A–B)
= 1/2 [cos (100o + 20o) + cos (100o – 20o) + cos (140o + 100o) + cos (140o – 100o) – cos (200o + 140o) – cos (200o – 140o)]]
= 1/2 [cos 120o + cos 80o + cos 240o + cos 40o – cos 340o – cos 60o]
= 1/2 [cos (90o + 30o) + cos 80o + cos (180o + 60o) + cos 40o – cos (360o – 20o) – cos 60o]
= 1/2 [–sin 30o + cos 80o – cos 60o + cos 40o – cos 20o – cos 60o]
= 1/2 [–sin 30o + cos 80o + cos 40o – cos 20o – 2 cos 60o]
= 1/2 [–sin 30o + 2 cos (80o+40o)/2 cos (80o–40o)/2 – cos 20o – 2 × 1/2]
= 1/2 [–sin 30o + 2 cos 120o/2 cos 40o/2 – cos 20o – 1]
= 1/2 [–sin 30o + 2 cos 60o cos 20o – cos 20o – 1]
= 1/2 [–1/2 + 2×(1/2)×cos 20o – cos 20o – 1]
= 1/2 [–1/2 + cos 20o – cos 20o – 1]
= 1/2 [–1/2 –1]
= 1/2 [–3/2]
= –3/4
= R.H.S.
Hence proved.
(vi) sin x/2 sin 7x/2 + sin 3x/2 sin 11x/2 = sin 2x sin 5x
Solution:
Given L.H.S. = sin x/2 sin 7x/2 + sin 3x/2 sin 11x/2
= 1/2 [2 sin 7x/2 sin x/2 + 2 sin 11x/2 sin 3x/2]
We know, 2 sin A sin B = cos (A–B) – cos (A+B)
= 1/2 [cos (7x/2 – x/2) – cos (7x/2 + x/2) + cos (11x/2 – 3x/2) – cos (11x/2 + 3x/2)]
= 1/2 [cos (7x–x)/2 – cos (7x+x)/2 + cos (11x–3x)/2 – cos (11x+3x)/2]
= 1/2 [cos 6x/2 – cos 8x/2 + cos 8x/2 – cos 14x/2]
= 1/2 [cos 3x – cos 7x]
= –1/2 [cos 7x – cos 3x]
= –1/2 [–2 sin (7x+3x)/2 sin (7x–3x)/2]
= –1/2 [–2 sin 10x/2 sin 4x/2]
= –1/2 [–2 sin 5x sin 2x]
= –2/–2 sin 5x sin 2x
= sin 2x sin 5x
= R.H.S.
Hence proved.
(vii) cos x cos x/2 – cos 3x cos 9x/2 = sin 4x sin 7x/2
Solution:
Given L.H.S. = cos x cos x/2 – cos 3x cos 9x/2
= 1/2 [2 cos x cos x/2 – 2 cos 9x/2 cos 3x]
We know, 2 cos A cos B = cos (A+B) + cos (A–B)
= 1/2 [cos (x + x/2) + cos (x – x/2) – cos (9x/2 + 3x) – cos (9x/2 – 3x)]
= 1/2 [cos (2x+x)/2 + cos (2x–x)/2 – cos (9x+6x)/2 – cos (9x–6x)/2]
= 1/2 [cos 3x/2 + cos x/2 – cos 15x/2 – cos 3x/2]
= 1/2 [cos x/2 – cos 15x/2]
= – 1/2 [cos 15x/2 – cos x/2]
= – 1/2 [–2 sin (15x/2 + x/2)/2 sin (15x/2 – x/2)/2]
= -1/2 [–2 sin (16x/2)/2 sin (14x/2)/2]
= -1/2 [–2 sin 16x/4 sin 7x/2]
= – 1/2 [–2 sin 4x sin 7x/2]
= –2/–2 [sin 4x sin 7x/2]
= sin 4x sin 7x/2
= R.H.S.
Hence proved.
Question 7. Prove that:
(i) 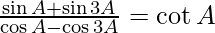
Solution:
We have,
L.H.S. = 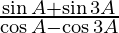
= 
= 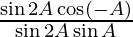
= 
= cot A
= R.H.S.
Hence proved.
(ii) 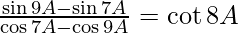
Solution:
We have,
L.H.S. = 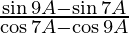
= 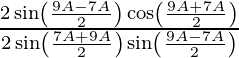
= 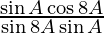
= cot 8A
= R.H.S.
Hence proved.
(iii)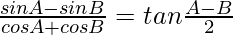
Solution:
We have,
L.H.S. =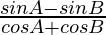
=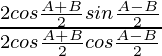
=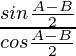
=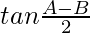
= R.H.S.
Hence proved.
(iv)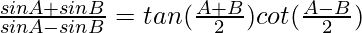
Solution:
We have,
L.H.S. =
=
=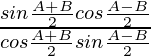
=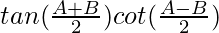
= R.H.S.
Hence proved.
(iv)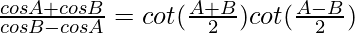
Solution:
We have,
L.H.S. =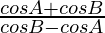
=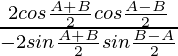
=
=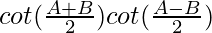
= R.H.S.
Hence proved.
Question 8. Prove that:
(i) 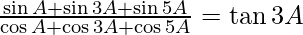
Solution:
We have,
L.H.S. = 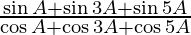
= 
= 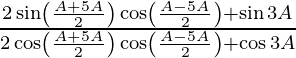
= 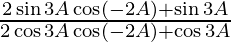
= 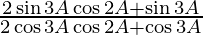
= ![Rendered by QuickLaTeX.com \frac{\sin 3A \left[ 2\cos 2A + 1 \right]}{\cos 3A \left[ 2\cos 2A + 1 \right]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3e67af36fea372c23535555a7f6fe227_l3.png)
= tan 3A
= R.H.S.
Hence proved.
(ii)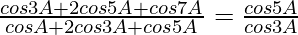
Solution:
We have,
L.H.S. =
=
=
=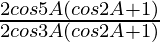
=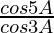
= R.H.S.
Hence proved.
(iii) 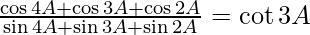
Solution:
We have,
L.H.S. = 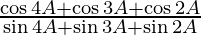
= 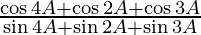
= 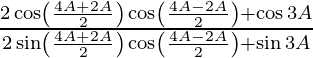
= 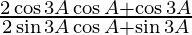
= ![Rendered by QuickLaTeX.com \frac{\cos 3A\left[ 2\cos A + 1 \right]}{\sin 3A\left[ 2\cos A + 1 \right]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5795888605b11505bd78ae763cc1ae4f_l3.png)
= cot 3A
= R.H.S.
Hence proved.
(iv) 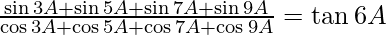
Solution:
We have,
L.H.S. = 
= 
= 
= 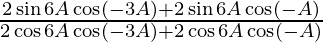
= 
= ![Rendered by QuickLaTeX.com \frac{2\sin 6A\left[ \cos 3A + \cos A \right]}{2\cos 6A\left[ \cos 3A + \cos A \right]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cd2bb6d10c47154d6a0edcc602a124a4_l3.png)
= tan 6A
= R.H.S.
Hence proved.
(v) 
Solution:
We have,
L.H.S. = 
= 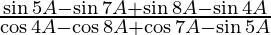
= 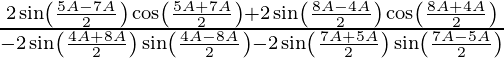
= 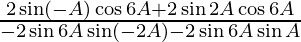
= 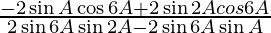
= ![Rendered by QuickLaTeX.com \frac{2\cos 6A\left[ \sin 2A - \sin A \right]}{2\sin 6A\left[ \sin 2A - \sin A \right]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0a4a99a60fcd4dbc55354a51141cda3a_l3.png)
= cot 6A
= R.H.S.
Hence proved.
(vi) 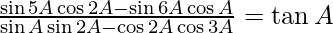
Solution:
We have,
L.H.S. = 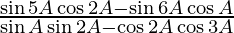
Multiplying numerator and denominator by 2, we get
= 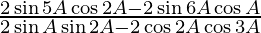
= 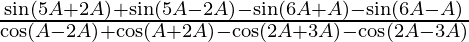
= 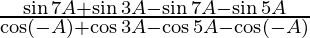
= 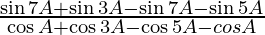
= 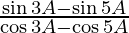
= 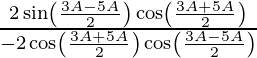
= 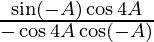
= 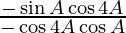
= 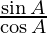
= tan A
= R.H.S.
Hence proved.
(vii)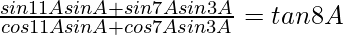
Solution:
We have,
L.H.S. =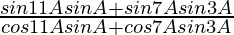
=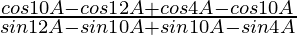
=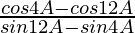
=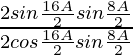
=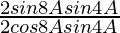
= tan 8A
= R.H.S.
Hence proved.
(viii) 
Solution:
We have,
L.H.S. = 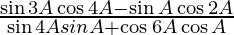
On multiplying numerator and denominator by 2, we get
= 
= 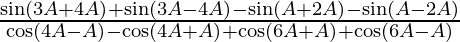
= 
= 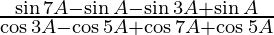
= 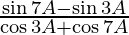
= 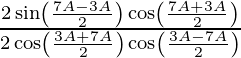
= 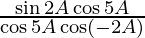
= 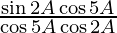
= tan 2A
= R.H.S.
Hence proved.
(ix) 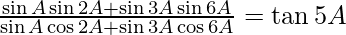
Solution:
We have,
L.H.S. = 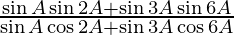
On multiplying numerator and denominator by 2, we get
= 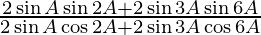
= 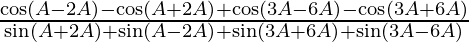
= 
= 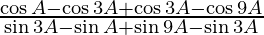
= 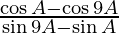
= 
= 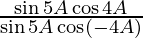
= tan 5A
= R.H.S.
Hence proved.
(x) 
Solution:
We have,
L.H.S. = 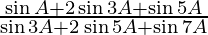
= 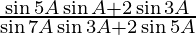
= 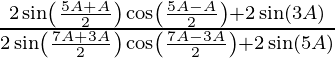
= 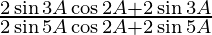
= 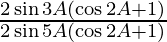
= sin3A/sin5A
= R.H.S.
Hence proved.
(xi)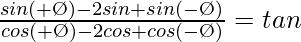
Solution:
We have,
L.H.S. =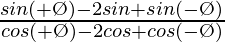
=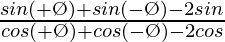
=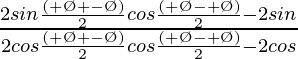
=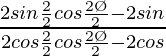
=
=
=
= tan θ
= R.H.S.
Hence proved.
Question 9. Prove that:
(i) sin α + sin β + sin γ – sin (α + β + γ) = 4 sin (α + β)/2 sin (β + γ)/2 sin (α + γ)/2
Solution:
We have,
L.H.S. = sin α + sin β + sin γ – sin (α + β + γ)
=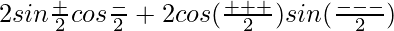
=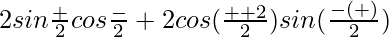
=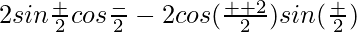
=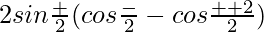
=
=
= 4 sin (α + β)/2 sin (β + γ)/2 sin (α + γ)/2
= R.H.S.
Hence proved.
(ii) cos (A + B + C) + cos (A – B + C) + cos (A + B – C) + cos (–A + B + C) = 4 cos A cos B cos C
Solution:
We have,
L.H.S. = cos (A + B + C) + cos (A – B + C) + cos (A + B – C) + cos (–A + B + C)
=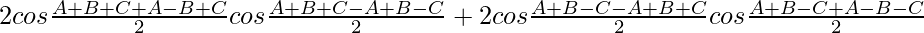
=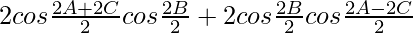
= 2 cos (A + C) cos B + 2 cos B cos (A − C)
= 2 cos B [cos (A + C) + cos (A − C)]
= 2 cos B![Rendered by QuickLaTeX.com \left[2cos\frac{A+C+A-C}{2}cos\frac{A+C-A+C}{2}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bff760f20b207904762e627b0b53ecd6_l3.png)
= 2 cos B [2 cos A cos C]
= 4 cos A cos B cos C
= R.H.S.
Hence proved.
Question 10. If cos A + cos B = 1/2 and sin A + sin B = 1/4, prove that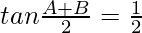 .
.
Solution:
We have,
cos A + cos B = 1/2
sin A + sin B = 1/4
=>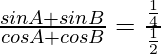
=>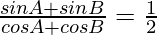
=>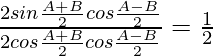
=>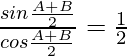
=>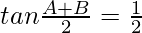
Hence proved.
Share your thoughts in the comments
Please Login to comment...