Question 1. What does the equation (x – a)2 + (y – b)2 = r2 become when the axes are transferred to parallel axes through the point (a–c, b)?
Solution:
We are given,
(x – a)2 + (y – b)2 = r2
Putting x = X + a – c and y = Y + b, we get,
=> ((X + a – c) – a)2 + ((Y + b ) – b)2 = r2
=> (X – c)2 + Y2 = r2
=> X2 + c2 – 2cX + Y2 = r2
=> X2 + Y2 – 2cX = r2 – c2
Therefore the required equation is X2 + Y2 – 2cX = r2 – c2.
Question 2. What does the equation (a – b) (x2 + y2) – 2abx = 0 become if the origin is shifted to the point (ab/(a–b), 0) without rotation?
Solution:
We are given,
(a – b) (x2 + y2) – 2abx = 0
Putting x = X + [ab/(a–b)] and y = Y, we get,
=> ![Rendered by QuickLaTeX.com (a - b)\left[\left(X+\frac{ab}{a+b}\right)^2 + Y^2\right] - 2ab\left(X+\frac{ab}{a+b}\right) = 0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-14139dd548f93aea8ab54f063a1db932_l3.png)
=> ![Rendered by QuickLaTeX.com (a-b)\left[X^2+\left(\frac{ab}{a+b}\right)^2+2\frac{Xab}{a+b}+Y^2\right]-2abX-2\frac{(ab)^2}{a-b} = 0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2c22502de2cdb8646620ce45a445824d_l3.png)
=> ![Rendered by QuickLaTeX.com (a-b)\left[\frac{X^2(a-b)^2+(ab)^2+2Xab(a-b)+Y^2(a-b)^2}{(a-b)^2}\right]-\frac{2abX(a-b)+2(ab)^2}{a-b}= 0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c9b9f3beca64881d83fd8622e9b8f62f_l3.png)
=> 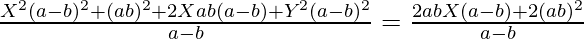
=> X2 (a–b)2 + (ab)2 + 2abX (a–b)+Y2 (a–b)2 = 2abX (a–b)+2(ab)2
=> (a – b)2 (X2 + Y2) = a2b2
Therefore the required equation is (a – b)2 (X2 + Y2) = a2b2.
Question 3. Find what the following equations become when the origin is shifted to the point (1, 1)?
(i) x2 + xy – 3x – y + 2 = 0
Solution:
We are given,
x2 + xy – 3x – y + 2 = 0
Putting x = X + 1 and y = Y + 1, we get,
=> (X + 1)2 + (X + 1) (Y + 1) – 3(X + 1) – (Y + 1) + 2 = 0
=> X2 + 1 + 2X + XY + X + Y + 1 – 3X – 3 – Y – 1 + 2 = 0
Therefore the required equation is X2 + XY = 0.
(ii) x2 – y2 – 2x + 2y = 0
Solution:
We are given,
x2 – y2 – 2x + 2y = 0
Putting x = X + 1 and y = Y + 1, we get,
=> (X + 1)2 – (Y + 1)2 – 2(X + 1) + 2(Y + 1) = 0
=> X2 + 1 + 2X – Y2 – 1 – 2Y – 2X – 2 + 2Y + 2 = 0
=> X2 – Y2 = 0
Therefore the required equation is X2 – Y2 = 0.
(iii) xy – x – y + 1 = 0
Solution:
We are given,
xy – x – y + 1 = 0
Putting x = X + 1 and y = Y + 1, we get,
=> (X + 1) (Y + 1) – (X + 1) – (Y + 1) + 1 = 0
=> XY + X + Y + 1 – X – 1 – Y – 1 + 1 = 0
=> XY = 0
Therefore the required equation is XY = 0.
(iv) xy – y2 – x + y = 0
Solution:
We are given,
xy – y2 – x + y = 0
Putting x = X + 1 and y = Y + 1, we get,
=> (X + 1) (Y + 1) – (Y + 1)2 – (X + 1) + (Y + 1) = 0
=> XY + X + Y + 1 – Y2 – 1 – 2Y – X – 1 + Y + 1 = 0
=> XY – Y2 = 0
Therefore, the required equation is XY – Y2 = 0.
Question 4. At what point the origin be shifted so that the equation x2 + xy – 3x – y + 2 = 0 does not contain any first degree term and constant term?
Solution:
We are given,
x2 + xy – 3x – y + 2 = 0
Suppose (a, b) is the point where the origin has been shifted from (0, 0). Putting x = X + a and y = Y + b, we get the transformed equation,
=> (X + a)2 + (X + a)(Y + b) – 3(X + a) – (Y + b) + 2 = 0
=> X2 + a2 + 2aX + XY + aY + bX + ab – 3X – 3a – Y – b + 2 = 0
=> X2 + XY + X(2a + b – 3) + Y(a – 1) + a2 + ab – 3a – b + 2 = 0
As our transformed equation has no first-degree term, we have,
2a + b – 3 = 0 and a – 1 = 0
By solving these equations we have a = 1 and b = 1.
Therefore, the origin has been shifted to (1,1) from (0,0).
Question 5. Verify that the area of the triangle with vertices (2, 3), (5, 7), and (–3, –1) remains invariant under the translation of axes when the origin is shifted to the point (–1, 3).
Solution:
Here, L.H.S. = A1 = Area of the triangle with vertices (2, 3), (5, 7) and (–3, –1)
= 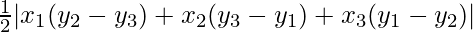
= 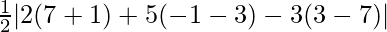
= 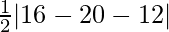
= 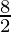
= 4 sq. units
As the origin shifted to point (–1, 3), the new coordinates of the triangle are:
(X1, Y1) = (2–1, 3+3) = (1, 6)
(X2, Y2) = (5–1, 7+3) = (4, 10)
(X3, Y3) = (–3–1, –1+3) = (–4, 2)
Now, R.H.S. = A2 = Area of the triangle with vertices (1, 6), (4, 10) and (–4, 2)
= 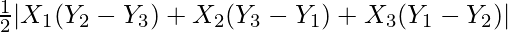
= 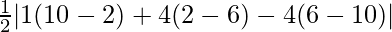
= 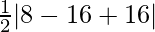
= 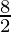
= 4 sq. units
Therefore, A1 = A2.
Hence, proved.
Question 6. Find what the following equations become when the origin is shifted to the point (1, 1)?
(i) x2 + xy – 3y2 – y + 2 = 0
Solution:
We are given,
x2 + xy – 3y2 – y + 2 = 0
Putting x = X + 1 and y = Y + 1, we get,
=> (X + 1)2 + (X + 1) (Y + 1) – 3(Y + 1)2 – (Y + 1) + 2 = 0
=> X2 + 1 + 2X + XY + X + Y + 1 – 3Y2 – 3 – 6Y – Y – 1 + 2 = 0
=> X2 – 3Y2 + XY + 3X – 6Y = 0
Therefore, the required equation is X2 – 3Y2 + XY + 3X – 6Y = 0.
(ii) xy – y2 – x + y = 0
Solution:
We are given,
xy – y2 – x + y = 0
Putting x = X + 1 and y = Y + 1, we get,
=> (X + 1) (Y + 1) – (Y + 1)2 – (X + 1)+ Y + 1 = 0
=> XY + X + Y + 1 – Y2 – 1 – 2Y – X – 1 + Y + 1 = 0
=> XY – Y2 = 0
Therefore, the required equation is XY – Y2 = 0.
(iii) xy – x – y + 1 = 0
Solution:
We are given,
xy – x – y + 1 = 0
Putting x = X + 1 and y = Y + 1, we get,
=> (X + 1) (Y + 1) – (Y + 1) – (X + 1) + 1 = 0
=> XY + X + Y + 1 – Y – 1 – X – 1 + 1 = 0
=> XY = 0
Therefore, the required equation is XY = 0.
(iv) x2 – y2 – 2x + 2y = 0
Solution:
We are given,
x2 – y2 – 2x + 2y = 0
Putting x = X + 1 and y = Y + 1, we get,
=> (X + 1)2 – (Y + 1)2 – 2(X + 1) + 2(Y + 1) = 0
=> X2 + 1 + 2X – Y2 – 1 – 2Y – 2X – 2 + 2Y + 2 = 0
=> X2 – Y2 = 0
Therefore, the required equation is X2 – Y2 = 0.
Question 7. Find the point to which the origin should be shifted after the translation of axes so that the following equations will have no first degree terms.
(i) x2 + y2 – 4x – 8y + 3 = 0
Solution:
We are given,
x2 + y2 – 4x – 8y + 3 = 0
Suppose (a, b) is the point where the origin has been shifted from (0, 0). Putting x = X + a and y = Y + b, we get the transformed equation,
=> (X + a)2 + (Y + b)2 – 4(X + a) – 8(Y + b) + 3 = 0
=> X2 + a2 + 2aX + Y2 + b2 + 2bY – 4X – 4a – 8Y – 8b + 3 = 0
=> X2 + Y2 + (2a – 4)X + (2b – 8)Y + (a2 + b2 – 4a – 8b +3) = 0
As our transformed equation has no first-degree term, we have,
2a – 4 = 0 and 2b – 8 = 0
By solving these equations we have a = 2 and b = 4.
Therefore, the origin has been shifted to (2,4) from (0,0).
(ii) x2 + y2 – 5x + 2y – 5 = 0
Solution:
We are given,
x2 + y2 – 5x + 2y – 5 = 0
Suppose (a, b) is the point where the origin has been shifted from (0, 0). Putting x = X + a and y = Y + b, we get the transformed equation,
=> (X + a)2 + (Y + b)2 – 5(X + a) + 2(Y + b) – 5 = 0
=> X2 + a2 + 2aX + Y2 + b2 + 2bY – 5X – 5a + 2Y + 2b – 5 = 0
=> X2 + Y2 + (2a – 5)X + (2b + 2)Y + (a2 + b2 – 5a + 2b – 5) = 0
As our transformed equation has no first-degree term, we have,
2a – 5 = 0 and 2b + 2 = 0
By solving these equations we have a = 5/2 and b = –1.
Therefore, the origin has been shifted to (5/2, –1) from (0,0).
(iii) x2 – 12x + 4 = 0
Solution:
We are given,
x2 – 12x + 4 = 0
Suppose (a, b) is the point where the origin has been shifted from (0, 0). Putting x = X + a and y = Y + b, we get the transformed equation,
=> (X + a)2 – 12(X + a) + 4 = 0
=> X2 + a2 + 2aX – 12X – 12a + 4 = 0
=> X2 + (2a – 12)X + (a2 – 12a + 4) = 0
As our transformed equation has no first-degree term, we have,
=> 2a – 12 = 0
=> a = 6
Therefore, the origin has been shifted to (6,b) from (0,0) where b is any arbitrary value.
Question 8. Verify that the area of the triangle with vertices (4, 6), (7, 10), and (1, –2) remains invariant under the translation of axes when the origin is shifted to the point (–2, 1).
Solution:
Here, L.H.S. = A1 = Area of the triangle with vertices (4, 6), (7, 10) and (1, –2)
= 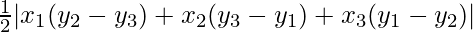
= 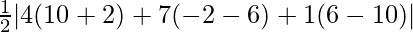
= 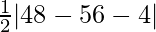
= 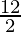
= 6 sq. units
As the origin shifted to point (–2, 1), the new coordinates of the triangle are:
(X1, Y1) = (4–2, 6+1) = (2, 7)
(X2, Y2) = (7–2, 10+1) = (5, 11)
(X3, Y3) = (1–2, –2+1) = (–1, –1)
Now, R.H.S. = A2 = Area of the triangle with vertices (2, 7), (5, 11), (–1, –1)
= 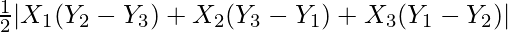
= 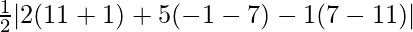
= 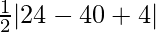
= 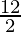
= 6 sq. units
Therefore, A1 = A2.
Hence, proved.
Share your thoughts in the comments
Please Login to comment...