Estimating Limits from Tables
Last Updated :
09 Sep, 2022
Limits tell us a lot about function behavior. They help mathematicians and engineers reason about the function their behavior and their properties. They form the basis for almost every important concept in calculus. Limits help us estimate the values function seems to be taking at a particular point. Often these limits are simple and can be calculated easily, but sometimes these limits evaluate to some indeterminable form, for solving them there are a lot of techniques and tricks. Solving limits using tables is one of the methods which works for almost every type of limit.
Limit
Limits are the values that the function apparently takes at a particular point. For a particular function f(x) defined on real numbers, the limit of the function at any point x = c is denoted as 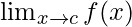 . Keep that in mind, limits are not the value of the function at a particular point, limit represents the value which function seems to be taking when one approaches the point. Usually, limits are approached from both the left-hand side and right-hand side of the point.
. Keep that in mind, limits are not the value of the function at a particular point, limit represents the value which function seems to be taking when one approaches the point. Usually, limits are approached from both the left-hand side and right-hand side of the point.
Often limits can be computed by a simple substitution, but sometimes some limits take some forms which are not defined. These forms are called indeterminable forms. Examples of indeterminable forms are 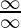 ,
, 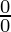 , 0 x ∞ etc.
, 0 x ∞ etc.
Using tables all these problems and forms can be avoided. Let’s look at that in detail.
Approximating Limits using Tables
Tables are a good tool that can be used to reason about the limits. Using tables also takes care of the indeterminable forms of the limit. This method involves calculating the value of the function at the points nearby the point at which we are supposed to calculate the limit. Estimating limits this way is a lot better than eyeballing the graphs of the functions. Let’s consider an example to see how this method works by taking a function f(x) = x – 1 and calculating the limit for this function at x = 0.
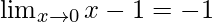
Let’s calculate this value using tables. The way is to calculate the value of the function at different values of x. The goal is to reach infinitely close to the target point but not at the target point. Keep in mind that while creating the table, the function should be approached from both the left-hand side and right-hand side.
Steps for calculating limits through tables:
- Start from the points which are infinitely close to the target point.
- Approach the target point from left and go infinitely close while evaluating the function for every point.
- Repeat the same thing from right-hand side.
The table that is created will have values that are almost equal, and will give an estimate of the limit at that point.
| x | f(x) |
| -0.1 | -1.1 |
| -0.05 | -1.05 |
| -0.001 | -1.001 |
| 0.001 | 0.999 |
| 0.05 | 0.95 |
Notice in the table, as we move closer and closer to x = 0 from either side, the value of the function approaches the value -1.
Thus, 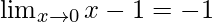
Note: While populating the table, some things must be kept in mind to get the right value of limit:
- Do not assume that the function value is the value of the limit. Sometimes there might be a discontinuity in the function, it might seem that function is going to take a particular value, but the actual value at that point is different. It often happens at the points where the function is either discontinuous or undefined.
- Approach from both sides of the point.
- Always go as close as possible to the point.
One-sided Limit from Tables
While asked for one-sided limits, tables are usually populated with values that are bot greater than and less than, then the point at which the limit is to be calculated. In other words, both left-hand and right-hand limits are to be calculated. In one-sided limits, tables are populated either with the left-hand side of the point or the right-hand side of the point.
Let’s see this through an example.
Example: Consider an example, for the function f(x) = x2. Calculate 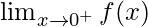
Solution:
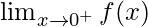
This means that value of right-hand side limit is asked. In this case, the table is populated only from the values which lie on the right-hand side of x = 0.
| x | f(x) |
| 0.1 | 0.01 |
| 0.05 | 0.0025 |
| 0.001 | 0.000001 |
| 0.0005 | 0.00000025 |
| 0.0001 | 0.00000001 |
Notice from the table that the value of the limit is approaching the value 0.
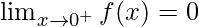
Let’s see some problems with this concept.
Sample Problems
Question 1: Consider an example, for the function f(x) = x2 Calculate 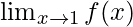
Solution:
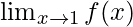
This means that value of right-hand side limit is asked. In this case, the table is populated only from the values which lie on the right-hand side of x = 1.
| x | f(x) |
| 0.9 | 0.81 |
| 0.95 | 0.9025 |
| 0.99 | 0.9801 |
| 0.999 | 0.99801 |
| 1.001 | 1.002 |
| 1.01 | 1.02 |
Notice from the table that the value of the limit is approaching the value 1.
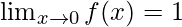
Question 2: Consider an example, for the function f(x) = 5x. Calculate 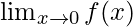
Solution:
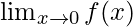
This means that value of right-hand side limit is asked. In this case, the table is populated only from the values which lie on the right-hand side of x = 0.
| x | f(x) |
| -0.1 | -0.5 |
| -0.05 | -0.25 |
| -0.001 | -0.005 |
| 0.001 | 0.005 |
| 0.01 | 0.05 |
Notice from the table that the value of the limit is approaching the value 0.
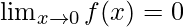
Question 3: Consider an example, for the function f(x) = 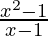 . Calculate
. Calculate 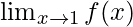
Solution:
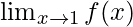
This means that value of right-hand side limit is asked. In this case, the table is populated only from the values which lie on the right-hand side of x = 1.
| x | f(x) |
| 0.999 | 1.999 |
| 0.9999 | 1.9999 |
| 0.99999 | 1.99999 |
| 1.00001 | 2.00001 |
| 1.0001 | 2.0001 |
Notice from the table that the value of the limit is approaching the value 2.
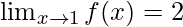
Question 4: Consider an example, for the function f(x) = 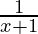 . Calculate
. Calculate 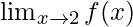
Solution:
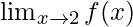
This means that value of right-hand side limit is asked. In this case, the table is populated only from the values which lie on the right-hand side of x = 2.
| x | f(x) |
| 1.999 | 0.33344448 |
| 1.9999 | 0.33334444 |
| 1.99999 | 0.33333444 |
| 2.00001 | 0.33333222 |
| 2.0001 | 0.33332222 |
Notice from the table that the value of the limit is approaching the value 0.333.
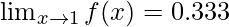
Question 5: Consider an example, for the function f(x) = 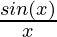 . Calculate
. Calculate 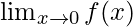
Solution:
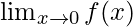
This means that value of right-hand side limit is asked. In this case, the table is populated only from the values which lie on the right-hand side of x = 0.
| x | f(x) |
| -0.1 | 0.99833 |
| -0.01 | 0.99998 |
| -0.001 | 0.99999 |
| 0.001 | 0.99999 |
| 0.01 | 0.99998 |
Notice from the table that the value of the limit is approaching the value 1.
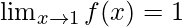
Question 6: Consider an example, for the function f(x) = |x|. Calculate 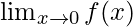
Solution:
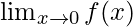
This means that value of right-hand side limit is asked. In this case, the table is populated only from the values which lie on the right-hand side of x = 0.
| x | f(x) |
| -0.1 | 0.1 |
| -0.01 | 0.01 |
| -0.001 | 0.001 |
| 0.001 | 0.001 |
| 0.01 | 0.01 |
Notice from the table that the value of the limit is approaching the value 0.
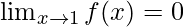
Question 7: Consider an example, for the function f(x) = log(x). Calculate 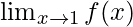
Solution:
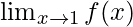
This means that value of right-hand side limit is asked. In this case, the table is populated only from the values which lie on the right-hand side of x = 1.
| x | f(x) |
| 0.999 | 0.000434 |
| 0.9999 | 0.0000434 |
| 0.99999 | 0.00000434 |
| 1.00001 | 0.00000434 |
| 1.0001 | 0.0000434 |
Notice from the table that the value of the limit is approaching the value 0.
Share your thoughts in the comments
Please Login to comment...