Question 1. Find the 11th term from the beginning and the 11th term from the end in the expansion of (2x – 1/x2)25.
Solution:
We are given, (2x – 1/x2)25.
The given expression contains 25 + 1 = 26 terms.
So, the 11th term from the end is the (26 − 11 + 1) th term = 16th term from the beginning.
Hence, T16 = T15+1 = 25C15 (2x)25-15 (−1/x2)15
= 25C15 (210) (x)10 (−1/x30)
= – 25C15 (210/ x20)
Now, the 11th term from the beginning is,
T11 = T10+1 = 25C10 (2x)25-10 (−1/x2)10
= 25C10 (215) (x)15 (1/x20)
= 25C10 (215/ x5)
Question 2. Find the 7th term in the expansion of (3x2 – 1/x3)10.
Solution:
We are given, (3x2 – 1/x3)10.
The 7th term of the expression is given by,
T7 = T6+1
= 10C6 (3x2)10−6 (−1/x3)6
= 10C6 (3)4 (x)8 (1/x18)
= 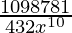
= 17010/ x10
Question 3. Find the 5th term from the end in the expansion of (3x – 1/x2)10.
Solution:
We are given, (3x – 1/x2)10
The 5th term from the end is the (11 – 5 + 1)th = 7th term from the beginning.
So, T7 = T6+1
= 10C6 (3x)10-6 (–1/x2)6
= 10C6 (3)4 (x)4 (1/x12)
= 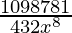
= 17010/ x8
Question 4. Find the 8th term in the expansion of (x3/2 y1/2 – x1/2 y3/2)10.
Solution:
We are given, (x3/2 y1/2 – x1/2 y3/2)10.
The 8th term of the expression is given by,
T8 = T7+1
= 10C7 (x3/2 y1/2)10–7 (–x1/2 y3/2)7
= 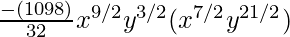
= –120 x8y12
Question 5. Find the 7th term in the expansion of (4x/5 + 5/2x)8.
Solution:
We are given, (4x/5 + 5/2x)8.
The 8th term of the expression is given by,
T7 = T6+1
= 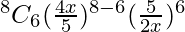
= 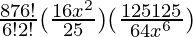
= 4375/ x4
Question 6. Find the 4th term from the beginning and 4th term from the end in the expansion of (x + 2/x)9.
Solution:
We are given, (x + 2/x)9.
The given expression contains 9 + 1 = 10 terms.
So, the 4th term from the end is the (10 − 4 + 1) th term = 7th term from the beginning.
Hence, T7 = T6+1 = 9C6 (x)9-6 (2/x)6
= 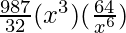
= 5376/ x3
Now, the 4th term from the beginning is,
T4 = T3+1 = 9C3 (2x)9-3 (2/x)3
= 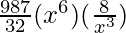
= 672 x3
Question 7. Find the 4th term from the end in the expansion of (4x/5 – 5/2x)9.
Solution:
We are given, (4x/5 – 5/2x)9
The 4th term from the end is (10 − 4 + 1)th term = 7th term, from the beginning.
T7 = T6+1
= 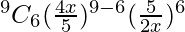
= 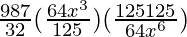
= 10500/ x3
Question 8. Find the 7th term from the end in the expansion of (2x2 – 3/2x)8.
Solution:
We are given, (2x2 – 3/2x)8
The 7th term from the end is (9 − 7 + 1)th term = 3rd term, from the beginning.
T3 = T2+1
= 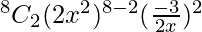
= 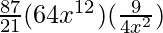
= 4032 x10
Question 9. Find the coefficient of:
(i) x10 in the expansion of (2x2 – 1/x)20
Solution:
We are given, (2x2 – 1/x)20
We know, the (r+1)th term of the expression is given by,
Tr+1 = nCr xn-r ar
= 20Cr (2x2)20-r (-1/x)r
= (-1)r 20Cr (2)20-r x40-2r-r
If x10 exists in the expansion, we must have,
=> 40 − 3r = 10
=> 3r = 30
=> r = 10
Coefficient of x10 = (-1)10 20C10 (2)20-10
= 20C10 (2)10
(ii) x7 in the expansion of (x – 1/x2)40
Solution:
We are given, (x – 1/x2)40
We know, the (r+1)th term of the expression is given by,
Tr+1 = nCr xn-r ar
= 40Cr (x)40-r (-1/x2)r
= (-1)r 40Cr x40-r-2r
If x7 exists in the expansion, we must have,
=> 40 − 3r = 7
=> 3r = 33
=> r = 11
Coefficient of x7 = (-1)11 40C11
= − 40C11
(iii) x-15 in the expansion of (3x2 – a/3x3)10
Solution:
We are given, (3x2 – a/3x3)10
We know, the (r+1)th term of the expression is given by,
Tr+1 = nCr xn-r ar
= 10Cr (3x2)10-r (a/3x3)r
= (-1)r 10Cr 310-r-r x20-2r-3r ar
If x-15 exists in the expansion, we must have,
=> 20 − 5r = −15
=> 5r = 35
=> r = 7
Coefficient of x-15 = (-1)7 10C7 310-14 a7
= 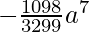
= −40a7/27
(iv) x9 in the expansion of (x2 – 1/3x)9
Solution:
We are given, (x2 – 1/3x)9
We know, the (r+1)th term of the expression is given by,
Tr+1 = nCr xn-r ar
= 9Cr (x2)9-r (-1/3x)r
= (-1)r 9Cr x18-2r-r (1/3)r
If x9 exists in the expansion, we must have,
=> 18 − 3r = 9
=> 3r = 9
=> r = 3
Coefficient of x9 = (-1)3 9C3 (1/3)3
= 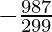
= −28/9
(v) xm in the expansion of (x + 1/x)n
Solution:
We are given, (x + 1/x)n
We know, the (r + 1)th term of the expression is given by,
Tr+1 = nCr xn- r (1/xr)
= nCr xn- 2r
If xm exists in the expansion, we must have,
=> n – 2r = m
=> r = (n – m)/2
Coefficient of xm = nC(n-m)/2
= 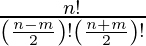
(vi) x in the expansion of (1 – 2x3 + 3x5) (1 + 1/x)8
Solution:
We are given, (1 – 2x3 + 3x5) (1 + 1/x)8
We know, the (r + 1)th term of the expression is given by,
= (1 – 2x3 + 3x5) (8C0 + 8C1 (1/x) + 8C2 (1/x2) + 8C3 (1/x3) + 8C4 (1/x4) + 8C5 (1/x5) + 8C6 (1/x6) + 8C7 (1/x7) + 8C8 (1/x8))
Here, x appear in the above expression at -2 x3 8C2 (1/x2) + 3x5.8C4 (1/x4)
So, coefficient of x = 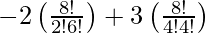
= – 56 + 210
= 154
(vii) a5b7 in the expansion of (a – 2b)12
Solution:
We are given, (a – 2b)12
We know, the (r+1)th term of the expression is given by,
Tr+1 = nCr xn-r ar
= (-1)r 12Cr (a)12-r (2b)r
If a5b7 exists in the expansion, we must have,
=> 12 − r = 5
=> r = 7
Coefficient of a5b7 = (-1)7 12C7 (2)7
= 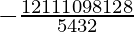
= − 101376
(viii) x in the expansion of (1 – 3x + 7 x2) (1 – x)16
Solution:
We are given, (1 – 3x + 7 x2) (1 – x)16
We know, the (r + 1)th term of the expression is given by,
= (1 – 3x + 7x2) (16C0 + 16C1 (-x) + 16C2 (-x)2 + 16C3 (-x)3+ 16C4 (-x)4 + 16C5 (-x)5 + 16C6 (-x)6 + 16C7 (-x)7 + 16C8 (-x)8 + 16C9 (-x)9 + 16C10 (-x)10 + 16C11 (-x)11 + 16C12 (-x)12 + 16C13 (-x)13 + 16C14 (-x)14 + 16C15 (-x)15 + 16C16 (-x)16)
Here, x appear in the above expression at 16C1 (-x) – 3x 16C0
So, the coefficient of x = 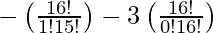
= – 16 – 3
= – 19
Question 10. Which term in the expansion of ![Rendered by QuickLaTeX.com \left[\left(\frac{x}{\sqrt{y}}\right)^{\frac{1}{3}}+\left(\frac{x}{\sqrt[3]{y}}\right)^{\frac{1}{2}}\right]^{21}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f60410ea35cfa28c9102e34baee43d9f_l3.png) contains x and y to one and the same power.
contains x and y to one and the same power.
Solution:
We are given, ![Rendered by QuickLaTeX.com \left[\left(\frac{x}{\sqrt{y}}\right)^{\frac{1}{3}}+\left(\frac{x}{\sqrt[3]{y}}\right)^{\frac{1}{2}}\right]^{21}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ad8206c5d53f7741b2c81dbd49d8e53a_l3.png)
We know, the (r+1)th term of the expression is given by,
Tr+1 = nCr xn-r ar
= ![Rendered by QuickLaTeX.com ^{21}C_r\left[(\frac{x}{\sqrt{y}})^{\frac{1}{3}}\right]^{21-r}\left[(\frac{y}{\sqrt[3]x})^{\frac{1}{2}}\right]^{r}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-068535566884b2e93d65961747f94ac5_l3.png)
= 21Cr x7-r/2 y2r/3-7/2
If x and y have same power, we must have,
=> 7 − r/2 = 2r/3 − 7/2
=> 7r/6 = 21/2
=> r = 9
Hence the required term is 9 + 1 = 10th term.
Question 11. Does the expansion of (2x2 – 1/x)20 contain any term involving x9?
Solution:
We are given, (2x2 – 1/x)20
We know, the (r+1)th term of the expression is given by,
Tr+1 = nCr xn-r ar
= 20Cr (2x2)20-r (1/x)r
= 20Cr (2)20-r x40-2r-r
If x9 exists in the expansion, we must have,
=> 40 − 3r = 9
=> 3r = 31
=> r = 31/3
It is not possible, since r is not an integer.
Hence, there is no term with x9 in the given expansion.
Question 12. Show that the expansion of (x2 + 1/x)12 does not contain any term involving x-1.
Solution:
We have, (x2 + 1/x)12
We know, the (r+1)th term of the expression is given by,
Tr+1 = nCr xn-r ar
= 12Cr (x2)12-r (1/x)r
= 12Cr x24-2r-r
For this term to contain x-1, we must have
=> 24 – 3r = −1
=> 3r = 24 + 1
=> 3r = 25
=> r = 25/3
It is not possible, since r is not an integer.
Hence, there is no term with x-1 in the given expansion.
Question 13. Find the middle term in the expansion of:
(i) (2/3x – 3/2x)20
Solution:
We have,
(2/3x – 3/2x)20 where, n = 20 (which is an even number)
So, the middle term is (n/2 + 1) = (20/2 + 1) = (10 + 1) = 11th term
Now,
T11 = T10+1
= 20C10 (2/3x)20-10 (3/2x)10
= 20C10 (210/310) × (310/210) x10-10
= 20C10
(ii) (x2 – 2/x)10
Solution:
We have,
(x2 – 2/x)10 where, n = 10 (which is an even number)
So, the middle term is (n/2 + 1) = (10/2 + 1) = (5 + 1) = 6th term
Now,
T6 = T5+1
= 10C5 (x2)10-5 (-2/x)5
= 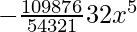
= − 8064 x5
(iii) (x/a – a/x)10
Solution:
We have,
(x/a – a/x)10 where, n = 10 (even number).
So the middle term is (n/2 + 1) = (10/2 + 1) = (5 + 1) = 6th term
Now,
T6 = T5+1
= 10C5 (x/a)10-5 (-a/x)5
= 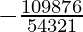
= −252
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...