Class 12 RD Sharma Solutions – Chapter 22 Differential Equations – Exercise 22.10 | Set 1

Solve the following differential equations:

Question 1. dy/dx + 2y = e^3x

Solution:

We have,

dy/dx + 2y = e^3x  ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = 2, Q = e^3x

So, I.F = e^∫Pdx

= e^∫2dx

= e^2x

The solution of differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(e^2x) = ∫e^3x.e^2xdx + c

y(e^2x) = (1/5)e^5x + c

y = (e^3x/5) + ce^-2x

Hence, this is the required solution.

Question 2. 4(dy/dx) + 8y = 5e^-3x

Solution:

We have,

4(dy/dx) + 8y = 5e^-3x

(dy/dx) + 2y = (5/4)e^-3x  ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = 2, Q = (5/4)e^-3x

So, I.F = e^∫Pdx

= e^∫2dx

= e^2x

The solution of differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(e^2x) = (5/4)∫e^-3x.e^2xdx + c

y(e^2x) = (5/4)∫e^-xdx + c

y = -(5/4)e^-3x + ce^-2x

This is the required solution.

Question 3. (dy/dx) + 2y = 6e^x

Solution:

We have,

(dy/dx) + 2y = 6e^x ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = 2, Q = 6e^x

So, I.F = e^∫Pdx

= e^∫2dx

= e^2x

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(e^2x) = ∫6e^x.e^2xdx + c

y(e^2x) = 6∫e^3xdx + c

y(e^2x) = 2e^3x + c

y = 2e^x + ce^-2x

This is the required solution.

Question 4. (dy/dx) + y = e^-2x

Solution:

We have,

(dy/dx) + y = e^-2x ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = 1, Q = e^-2x

So, I.F = e^∫Pdx

= e^∫dx

= e^x

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(e^x) = ∫e^-2x.e^xdx + c

y(e^x) = ∫e^-xdx + c

y(e^x) = -e^-x + c

y = -e^-2x + ce^-x

This is the required solution.

Question 5. x(dy/dx) = x + y

Solution:

We have,

x(dy/dx) = x + y

(dy/dx) = 1 + (y/x)

(dy/dx) – (y/x) = 1  ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = (-1/x), Q = 1

So, I.F = e^∫Pdx

= e^-∫(dx/x)

= e^-log(x)

= e^log(1/x)

= (1/x)

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(1/x) = ∫(1/x)dx + c

(y/x) = log|x| + c

y = xlog|x| + cx

This is the required solution.

Question 6. (dy/dx) + 2y = 4x

Solution:

We have,

(dy/dx) + 2y = 4x   ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = 2, Q = 4x

So,

I.F = e^∫Pdx

= e^∫2dx

= e^2x

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(e^2x) = ∫4x.e^2xdx + c

y(e^2x) = 4x∫e^2xdx – 4∫{(dx/dx)∫e^2xdx}dx + c

y(e^2x) = 2xe^2x – 2∫e^2xdx + c

y(e^2x) = 2xe^2x – e^2x + c

y = (2x – 1) + ce^-2x

This is the required solution.

Question 7. x(dy/dx) + y = xe^x

Solution:

We have,

x(dy/dx) + y = xe^x

(dy/dx) + (y/x) = e^x  ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = (1/x), Q = e^x

So,

I.F = e^∫Pdx

= e^∫(dx/x)

= e^log(x)

= x

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(x) = ∫x.e^xdx + c

xy = x∫e^xdx – {(dx/dx)∫e^xdx}dx + c

xy = xe^x – ∫e^xdx + c

xy = xe^x – e^x + c

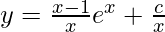
This is the required solution.

Question 8. (dy/dx) + [4x/(x² + 1)]y = -1/(x² + 1)²

Solution:

We have,

(dy/dx) + [4x/(x² + 1)]y = -1/(x² + 1)²    ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = [4x/(x² + 1)], Q = -1/(x² + 1)²

So,

I.F = e^∫Pdx

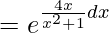
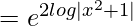
= (x²+1)²

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(x² + 1)² = ∫-[1/(x² + 1)²](x² + 1)²dx + c

y(x² + 1)² = -∫dx + c

y(x² + 1)² = -x + c

y = -x/(x² + 1)² + c/(x² + 1)²

This is the required solution.

Question 9. x(dy/dx) + y = xlogx

Solution:

We have,

x(dy/dx) + y = xlogx

(dy/dx) + (y/x) = logx  ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = (1/x), Q = logx

So,

I.F = e^∫Pdx

= e^∫(dx/x)

= e^log(x)

= x

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(x) = ∫x.logxdx + c

xy = logx∫xdx – {(d/dx)logx∫xdx}dx + c

xy = (x²/2)logx – ∫(1/x)(x²/2) + c

xy = (x²/2)logx – (1/2)∫xdx + c

xy = (x²/2)logx – (x²/4) + c

y = (x/2)logx – (x/4) + (c/x)

This is the required solution.

Question 10. x(dy/dx) – y = (x – 1)e^x

Solution:

We have,

x(dy/dx) – y = (x – 1)e^x

(dy/dx) – (y/x) = [(x – 1)/x]e^x  ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = -(1/x), Q = [(x – 1)/x]e^x

So,

I.F = e^∫Pdx

= e^-∫(dx/x)

= e^-log(x)

= e^log(1/x)

= 1/x

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

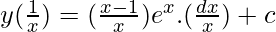
(y/x) = ∫[(1/x) – (1/x²)]e^x + c

Since, ∫[f(x) + f'(x)]e^xdx = f(x)e^x + c

(y/x) = (e^x/x) + c

y = e^x + xc

This is the required solution.

Question 11. (dy/dx) + y/x = x³

Solution:

We have,

(dy/dx) + y/x = x³     ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = 1/x, Q = x³

So, I.F = e^∫Pdx

= e^∫dx/x

= e^logx

= x

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

yx = ∫x³.xdx + c

yx = ∫x⁴dx + c

yx = (x⁵/5) + c

y = (x⁴/5) + c/x

This is the required solution.

Question 12. (dy/dx) + y = sinx

Solution:

We have,

(dy/dx) + y = sinx ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = 1, Q = sinx

So, I.F = e^∫Pdx

= e^∫dx

= e^x

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(e^x) = ∫sinx.e^xdx + c

Let, I = ∫sinx.e^xdx

I = e^x∫sinxdx – ∫{(d/dx)e^x∫sinxdx}dx

I = -e^xcos + ∫e^xcosxdx

I = -e^xcosx + e^x∫cosxdx – ∫{(d/dx)e^x∫cosxdx}dx

I = -e^xcosx + e^xsinx – ∫e^xsinxdx

2I = e^x(sinx – cosx)

I = (e^x/2)(sinx – cosx)

y(e^x) = (e^x/2)(sinx – cosx) + c

y = (1/2)(sinx – cosx) + ce^-x

This is the required solution.

Question 13. (dy/dx) + y = cosx

Solution:

We have,

(dy/dx) + y = cosx ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = 1, Q = cosx

So, I.F = e^∫Pdx

= e^∫dx

= e^x

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(e^x) = ∫cosx.e^xdx + c

Let, I = ∫cosx.e^xdx

I = e^x∫cosxdx – ∫{(d/dx)e^x∫cosxdx}dx

I = e^xsinx – ∫e^xsinxdx

I = e^xsinx – e^x∫sinxdx + ∫{(d/dx)e^x∫sinxdx}dx

I = e^xsinx + e^xcosx – ∫e^xcosxdx

2I = e^x(cosx + sinx)

I = (e^x/2)(cosx + sinx)

y(e^x) = (e^x/2)(cosx + sinx) + c

y = (1/2)(cosx + sinx) + ce^-x

This is the required solution.

Question 14. (dy/dx) + 2y = sinx

Solution:

We have,

(dy/dx) + 2y = sinx ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = 2, Q = sinx

So, I.F = e^∫Pdx

= e^∫2dx

= e^2x

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(e^2x) = ∫sinx.e^2xdx + c

Let, I = ∫sinx.e^2xdx

I = e^2x∫sinxdx – {(d/dx)e^2x∫sinxdx}dx

I = -e^2xcosx + 2∫e^2xcosdx

I = -e^2xcosx + 2e^2x∫cosxdx – 2{(d/dx)e^2x∫cosxdx}dx

I = -e^2xcosx + 2e^2xsinx – 4∫e^2xsinxdx

5I = e^2x(2sinx – cosx)

I = (e^2x/5)(2sinx – cosx)

y(e^2x) = (e^2x/5)(2sinx – cosx) + c

y = (1/5)(2sinx – cosx) + ce^-2x

This is the required solution.

Question 15. (dy/dx) – ytanx = -2sinx

Solution:

We have,

(dy/dx) – ytanx = -2sinx ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = -tanx, Q = sinx

So, 

I.F = e^∫Pdx

= e^∫-tanxdx

= e^-log|secx|

= 1/secx

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(1/secx) = -2∫sinx.(1/secx)dx + c

ycosx = -∫2sinx.cosxdx + c

ycosx = -∫sin2xdx + c

ycosx = (cos2x/2) + c

y = (cos2x/cosx) + (c/cosx)

This is the required solution.

Question 16. (1 + x²)(dy/dx) + y = tan^-1x

Solution:

We have,

(1 + x²)(dy/dx) + y = tan^-1x

(dy/dx) + [y/(1 + x²)] = tan^-1x/(1 + x²)  ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = 1/(1 + x²), Q = tan^-1x/(1 + x²)

So,

I.F = e^∫Pdx

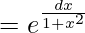
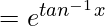
The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

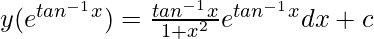
Let, tan^-1x = z

On differentiating both sides we get,

dx/(1 + x²) = dz

y(e^z) = ∫ze^zdz + c

y(e^z) = z∫e^zdz – {(dz/dz)∫e^zdz}dz

y(e^z) = ze^z – ∫ e^zdz + c

y(e^z) = e^z(z – 1) + c

y = (z – 1) + ce^-z

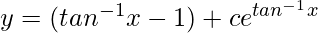
This is the required solution.

Question 17. (dy/dx) + ytanx = cosx

Solution:

We have,

(dy/dx) + ytanx = cosx  ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = tanx, Q = cosx

So, I.F = e^∫Pdx

= e^∫tanxdx

= e^log|secx|

= secx

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y.secx = ∫cosx.secxdx + c

y.secx = ∫dx + c

y.secx = x + c

y = xcosx + c.cosx

This is the required solution.

Question 18. (dy/dx) + ycotx = x²cotx + 2x

Solution:

We have,

(dy/dx) + ycotx = x²cotx + 2x ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = cotx, Q = x²cotx + 2x

So,

I.F = e^∫Pdx

= e^∫cotxdx

= e^log|sinx|

= sinx

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(sinx) = ∫(x²cotx + 2x)sinxdx + c

y(sinx) = ∫(x²cosx + 2xsinx)dx + c

y(sinx) = x²∫cosxdx – {(d/dx)x²∫cosxdx}dx + ∫2xsinxdx + c

y(sinx) = x²sinx – ∫2xsinxdx + ∫2xsinxdx + c

y(sinx) = x²sinxdx + c

This is the required solution.

Question 19. (dy/dx) + ytanx = x²cos²x

Solution:

We have,

(dy/dx) + ytanx = x²cos²x  ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = tanx, Q = x²cos²x

So,

I.F = e^∫Pdx

= e^∫tanxdx

= e^log|secx|

= secx

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(secx) = ∫secx.(x².cos²x)dx + c

y(secx) = ∫x².cosxdx + c

y(secx) = x²∫cosxdx – ∫{(d/dx)x²∫cosxdx}dx + c

y(secx) = x²sinx – 2∫xsinxdx + c

y(secx) = x²sinx – 2x∫sinxdx + 2∫{(dx/dx)∫sinxdx}dx + c

y(secx) = x²sinx + 2xcosx – 2∫cosxdx + c

y(secx) = x²sinx + 2xcosx – 2sinx + c

This is the required solution.

Question 20. (1 + x²)(dy/dx) + y =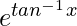 

Solution:

We have,

(1 + x²)(dy/dx) + y =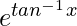 

(dy/dx) + [1/(x² + 1)]y = 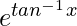/(x² + 1)  ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = 1/(x² + 1), Q = 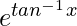/(x² + 1)

So,

I.F = e^∫Pdx

= 

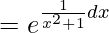
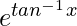
The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(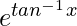) – ∫[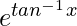/(x² + 1)]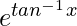dx + c

Let, tan^-1x = z

On differentiating both sides we get

dx/(1 + x²) = dz

ye^z = ∫e^2zdz + c

ye^z = (e^2z/2) + c

y = (e^z/z) + c.e^-z

y = (1/2)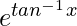 + c.

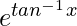
This is the required solution.

Question 21. xdy = (2y + 2x⁴ + x²)dx

Solution:

We have,

xdy = (2y + 2x⁴ + x²)dx

(dy/dx) = 2(y/x) + 2x³ + x

(dy/dx) – (y/x) = 2x³ + x   ………..(i)

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = -(2/x), Q = 2x³ + x

So,

I.F = e^∫Pdx

= e^-2∫(dx/x)

= e^-2log(x)

= e^2log|1/x|

= 1/x²

The solution of a differential equation is,

y(I.F) = ∫Q(I.F)dx + c

y(1/x²) = ∫(1/x²).(2x³ + x)dx + c

(y/x²) = ∫[2x + (1/x)]dx + c

(y/x²) = x² + log|x| + c

y = x⁴ + x²log|x| + cx²

This is the required solution.

Question 22. (1 + y²) + (x – 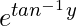)(dy/dx) = 0

Solution:

We have,

(1 + y²) + (x – 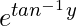)(dy/dx) = 0

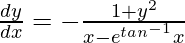
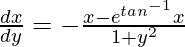
(dx/dy) + x/(1 + y²) = 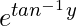/(1 + y²)  ………..(i)

The given equation is a linear differential equation of the form

(dx/dy) + Px = Q

Where, P = 1/(1 + y²), Q = 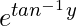/(1 + y²)

So,

I.F = e^∫Pdy

= 

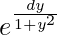
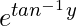
The solution of a differential equation is,

x(I.F) = ∫Q(I.F)dy + c

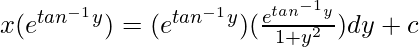
Let, tan^-1y = z

On differentiating both sides we have,

dy/(1 + y²) = dz

xe^z = ∫e^2zdz + c

xez = (e2z/2) + c

x = e^z/2 + ce^-z

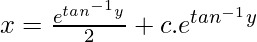
This is the required solution.

Question 23. y²(dx/dy) + x – 1/y = 0

Solution:

We have,

y²(dx/dy) + x – 1/y = 0

(dx/dy) + (x/y²) = 1/y³    ………..(i)

The given equation is a linear differential equation of the form

(dx/dy) + Px = Q

Where, P = 1/y², Q = 1/y³

So,

I.F = e^∫Pdy

= e^∫dy/y2

= e^-(1/y)

The solution of a differential equation is,

x(I.F) = ∫Q(I.F)dy + c

e^-(1/y)x = ∫(1/y³).(e^-1/y)dy + c

Let,-(1/y) = z

Differentiating both sides we have,

(dy/y²) = dz 

xe^z = -∫ze^zdz + c

xe^z = -z∫e^zdz + ∫{(dz/dz)∫e^zdz}dz + c

xe^z = -ze^z + ∫e^zdz + c

xe^z = -ze^z + e^z + c

x = (1 – z) + ce – z

x = [1 + (1/y)] + ce^1/y

x = (y + 1)/y + ce^1/y

This is the required solution.