Question 1. Find the equation of the plane which is parallel to 2x – 3y + z = 0 and passes through the point (1, –1, 2).
Solution:
We know that the equation of a plane parallel to 2x – 3y + z = 0 is given by:
2x – 3y + z + λ = 0
Since the plane passes through the point (1, –1, 2), we have:
2(1) – 3(–1) + 2 + λ = 0
⇒ λ = –7
On substituting the value of λ in the equation, we have:
2x – 3y + z + (-7) = 0
2x – 3y + z – 7= 0 is the required equation.
Question 2. Find the equation of the plane through (3, 4, –1) which is parallel to the plane 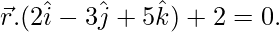
Solution:
The given plane passes through the vector 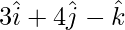 . Thus,
. Thus,
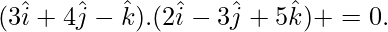
(3)(2) + (4)(-3) + (-1)(5) + λ = 0
⇒ λ = 11
On substituting the value of λ in the equation, we have:
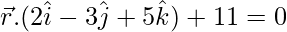 is the required equation.
is the required equation.
Question 3. Find the equation of the plane passing through the line of intersection of the planes 2x – 7y + 4z – 3 = 0 and 3x – 5y + 4z + 11 = 0 and the point (–2, 1, 3).
Solution:
The equation of the plane passing through the line of intersection of the given planes is:
(2x – 7y + 4z – 3) + λ(3x – 5y + 4z + 11) = 0
⇒ x(2 + 3λ) + y(–7 – 5λ) + z(4 + 4λ) – 3 + 11λ = 0
Also, since the plane passes through the point (–2, 1, 3), we have:
(–2)(2 + 3λ) + (1)(–7 – 5λ) + (3)(4 + 4λ) – 3 + 11λ = 0
⇒ λ = 1/6
On substituting the value of λ in the equation, we have:
x(2 + 3(1/6)) + y(–7 – 5(1/6)) + z(4 + 4(1/6)) – 3 + 11(1/6) = 0
15x – 47y + 28z = 7 is the required equation.
Question 4. Find the equation of the plane passing through the point 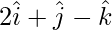 and passing through the line of intersection of the planes
and passing through the line of intersection of the planes 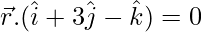 and
and 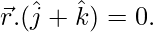
Solution:
The equation of the plane passing through the line of intersection of the given planes is:
![Rendered by QuickLaTeX.com \vec{r}.[(\hat{i}+3\hat{j}-\hat{k})+λ(\hat{j}+2\hat{k})]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3100dd2c2609ef75e5b5b25e586e42dc_l3.png)
Also, since the plane passes through point 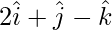 , we have:
, we have:
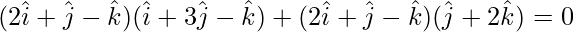
⇒ λ = 6
On substituting the value of λ in the equation, we have:
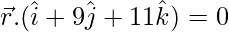 is the required equation.
is the required equation.
Question 5. Find the equation of the plane passing through the intersection of 2x – y = 0 and 3z – y = 0 and perpendicular to 4x + 5y – 3z = 8.
Solution:
The equation of the plane passing through the line of intersection of the given planes is:
2x – y + λ(3z – y) = 0
⇒ 2x + y(–1 – λ) + z(3λ) = 0
Since the planes are perpendicular, we have:
2(4) + (–5)(–1 – λ) + (–3)(3λ) = 0
⇒ λ = 3/14
On substituting the value of λ in the equation, we have:
2x + y(–1 – 3/14) + z(3(3/14)) = 0
28x – 17y + 9z = 0 is the required equation.
Question 6. Find the equation of the plane which contains the line of intersection of planes x + 2y + 3z – 4 = 0 and 2x + y – z + 5 = 0 and is perpendicular to the plane 5x + 3y – 6z + 8 = 0.
Solution:
The equation of the plane passing through the line of intersection of the given planes is:
x + 2y + 3z – 4 + λ(2x + y – z + 5) = 0
⇒ x(1 + 2λ) + y(2 + λ) + z(3 – λ) – 4 + 5λ = 0
Since the planes are perpendicular, we have:
5(1 + 2λ) + 3(2 + λ) + (–6)(3 – λ) = 0
⇒ λ = 7/19
On substituting the value of λ in the equation, we have:
x(1 + 2(7/19)) + y(2 + 7/19) + z(3 – 7/19) – 4 + 5(7/19) = 0
33x + 45y + 50z – 41 = 0 is the required equation.
Question 7. Find the equation of the plane passing through the line of intersection of the planes x + 2y + 3z + 4 = 0 and x – y + z + 3 = 0 and passing through the origin.
Solution:
The equation of the plane passing through the line of intersection of the given planes is:
x + 2y + 3z + 4 + λ(x – y + z + 3) = 0
⇒ x(1 + λ) + y(2 – λ) + z(3 + λ) + 4 + 3λ = 0
Also, since the plane passes through the origin, we have:
0(1 + λ) + 0(2 – λ) + 0(3 + λ) + 4 + 3λ = 0
⇒ λ = -4/3
On substituting the value of λ in the equation, we have:
x(1 + (-4/3)) + y(2 – (-4/3)) + z(3 + (-4/3)) + 4 + 3(-4/3) = 0
x – 10y – 5z = 0 is the required equation.
Question 8. Find the vector equation in scalar product form of the plane containing the line of intersection of the planes x – 3y + 2z – 5 = 0 and 2x – y + 3z – 1 = 0 and passing through (1, –2, 3).
Solution:
The equation of the plane passing through the line of intersection of the given planes is:
x – 3y + 2z – 5 + λ(2x – y + 3z – 1) = 0
⇒ x(1 + 2λ) + y(–3 – λ) + z(2 + 3λ) – 5 – λ = 0
Also, since the plane passes through the origin, we have:
1(1 + 2λ) + (–2)(–3 – λ) + 3(2 + 3λ) – 5 – λ = 0
⇒ λ = -2/3
On substituting the value of λ in the equation, we have:
x(1 + 2(-2/3)) + y(–3 – (-2/3)) + z(2 + 3(-2/3)) – 5 – (-2/3) = 0
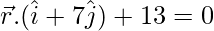 is the required equation.
is the required equation.
Question 9. Find the equation of the plane which contains the line of intersection of planes x + 2y + 3z – 4 = 0 and 2x + y – z + 5 = 0 and is perpendicular to the plane 5x + 3y + 6z + 8 = 0.
Solution:
The equation of the plane passing through the line of intersection of the given planes is:
x + 2y + 3z – 4 + λ(2x + y – z + 5) = 0
⇒ x(1 + 2λ) + y(2 + λ) + z(3 – λ) – 4 + 5λ = 0
We know that two planes are perpendicular when 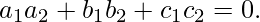
⇒ 5(1 + 2λ) + 3(2 + λ) + 6(3 – λ) = 0
⇒ λ = -29/7
On substituting the value of λ in the equation, we have:
x(1 + 2(-29/7)) + y(2 + (-29/7)) + z(3 – (-29/7)) – 4 + 5(-29/7) = 0
51x + 15y – 50z + 173 = 0 is the required equation.
Question 10. Find the equation of the plane passing through the line of intersection of the planes 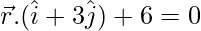 and
and 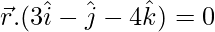 and which is at a unit distance from the origin.
and which is at a unit distance from the origin.
Solution:
The equation of the plane passing through the line of intersection of the given planes is:
x(1 + 3λ) + y(3 + λ) – 4zλ + 6 = 0
Distance from plane to the origin = 1
⇒ 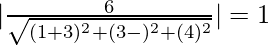
⇒ λ = ±1
Hence, 4x + 2y – 4z + 6 = 0 and –2x + 2y + 4z + 6 = 0 are the required equations.
Question 11. Find the equation of the plane passing through the line of intersection of the planes 2x + 3y – z + 1 = 0 and x + y – 2z + 3 = 0 and perpendicular to the plane 3x – 2y – z – 4 = 0.
Solution:
The equation of the plane passing through the line of intersection of the given planes is:
2x + 3y – z + 1 + λ(x + y – 2z + 3) = 0
⇒ x(2 + λ) + y(3 + λ) + z(–1 – 2λ) + 1 + 3λ = 0
We know that two planes are perpendicular when 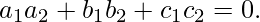
⇒ 3(2 + λ) + (–1)(3 + λ) + (–2)(–1 – 2λ) = 0
⇒ λ = -5/6
On substituting the value of λ in the equation, we have:
x(2 + (-5/6)) + y(3 + (-5/6)) + z(–1 – 2(-5/6)) + 1 + 3(-5/6) = 0
7x + 13y + 4z – 9 = 0 is the required equation.
Question 12. Find the equation of the plane that contains the line of intersection of the planes 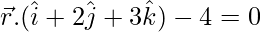 and
and 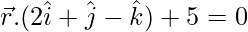 and which is perpendicular to the plane
and which is perpendicular to the plane 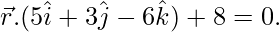
Solution:
The equation of the plane passing through the line of intersection of the given planes is:
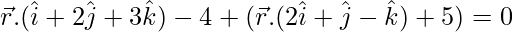
⇒ ![Rendered by QuickLaTeX.com \vec{r}.[(\hat{i}+2\hat{j}+3\hat{k})+λ(2\hat{i}+\hat{j}-\hat{k})]-4+5λ=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a2490e92e5fd9dcccf612cb68894dab9_l3.png)
We know that two planes are perpendicular if 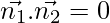
⇒ =0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4c645f858462346b01614d41d82bc327_l3.png)
⇒ 5(1 + 2λ) + 3(2 + λ) + (–6)(3 – λ) = 0
⇒ λ = 7/19
On substituting the value of λ in the equation, we have:
33x + 45y + 50z – 41 = 0 is the required equation.
Question 13. Find the vector equation of the plane passing through the intersection of planes 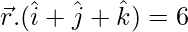 and
and 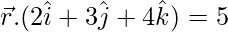 and the point (1, 1, 1).
and the point (1, 1, 1).
Solution:
The equation of the plane passing through the line of intersection of the given planes is:
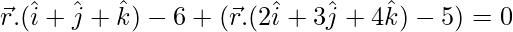
⇒ x(1 + 2λ) + y(1 + 3λ) +z(1 + 4λ) = 6 – 5λ
Also, since the plane passes through the point(1, 1, 1), we have:
1(1 + 2λ) + 1(1 + 3λ) +1(1 + 4λ) = 6 – 5λ
⇒ λ = 3/14
On substituting the value of λ in the equation, we have:
x(1 + 2(3/14)) + y(1 + 3(3/14)) +z(1 + 4(3/14)) = 6 – 5(3/14)
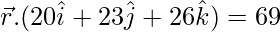 is the required equation.
is the required equation.
Question 14. Find the equation of the plane passing through the intersection of the planes 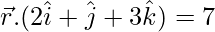 and
and 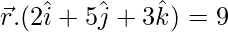 and the point (2, 1, 3).
and the point (2, 1, 3).
Solution:
The equation of the plane passing through the line of intersection of the given planes is:
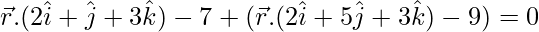
⇒ ![Rendered by QuickLaTeX.com \vec{r}.[(2+2λ)\hat{i}+(1+5λ)\hat{j}+(3+3λ)\hat{k}]-7-9λ=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b136406efeefb521030743b59e61f3b4_l3.png)
Also, since the plane passes through the point (2, 1, 3) we have:
9λ = –7
⇒ λ = -7/9
Substituting the value of λ in the equation, we have:
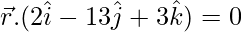 is the required equation.
is the required equation.
Question 15. Find the equation of the plane passing through the intersection of the planes 3x – y + 2z = 4 and x + y + z = 2 and the point (2, 2, 1).
Solution:
The equation of the plane passing through the line of intersection of the given planes is:
3x – y + 2z – 4 + λ(x + y + z – 2) = 0
Also, since the plane passes through the point (2, 2, 1), we have:
λ = -2/3
On substituting the value of λ in the equation, we have:
3x – y + 2z – 4 + (-2/3)(x + y + z – 2) = 0
7x – 5y + 4z = 0 is the required equation.
Question 16. Find the vector equation of the plane through the line of intersection of the planes x + 2y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0.
Solution:
The equation of the plane passing through the line of intersection of the given planes is:
x + 2y + z – 1 + λ(2x + 3y + 4z – 5) = 0
⇒ x(1 + 2λ) + y(1 + 3λ) +z(1 + 4λ) = 1 + 5λ
We know that two planes are perpendicular when 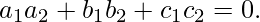
⇒ 1(1 + 2λ) + (–1)(1 + 3λ) + 1(1 + 4λ) = 1 + 5λ
⇒ λ = -1/3
On substituting the value of λ in the equation, we have:
x(1 + 2(-1/3)) + y(1 + 3(-1/3)) + z(1 + 4(-1/3)) = 1 + 5(-1/3)
x – z + 2 = 0 is the required equation.
Question 17. Find the equation of the plane passing through (a, b, c) and parallel to the plane 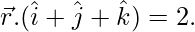
Solution:
Equation of the family of planes parallel to the given plane = 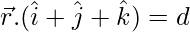
Since the plane passes through (a, b, c), we have:
a + b + c = d
Substituting the above equation in the equation of family of planes we have:
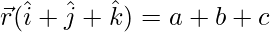
Hence, x + y + z = a + b + c is the required equation of the plane.
Share your thoughts in the comments
Please Login to comment...